备考2022年中考数学一轮复习(湘教版)专题35 几何图形与线段、 射线、 直线、角
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定2. 由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )
 A、18 B、15 C、12 D、63. 某立体图形的表面展开图如图所示,这个立体图形是( )
A、18 B、15 C、12 D、63. 某立体图形的表面展开图如图所示,这个立体图形是( )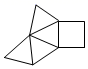 A、
A、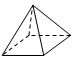 B、
B、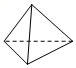 C、
C、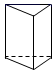 D、
D、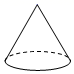 4. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′5. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )
4. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′5. 小光准备从A地去往B地,打开导航、显示两地距离为37.7km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( )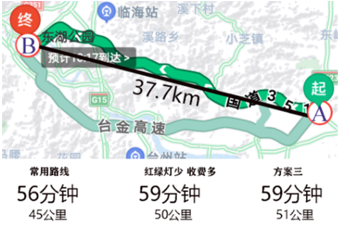 A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线6. 某几何体的展开图如图所示,该几何体是( )
A、两点之间,线段最短 B、垂线段最短 C、三角形两边之和大于第三边 D、两点确定一条直线6. 某几何体的展开图如图所示,该几何体是( )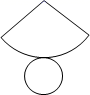 A、
A、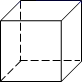 B、
B、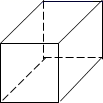 C、
C、 D、
D、 7. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或38. 下列图形是正方体展开图的个数为( )
7. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或38. 下列图形是正方体展开图的个数为( ) A、1个 B、2个 C、3个 D、4个9. 如图,点 在直线 上, .若 ,则 的大小为( )
A、1个 B、2个 C、3个 D、4个9. 如图,点 在直线 上, .若 ,则 的大小为( )
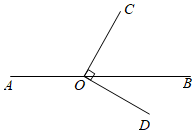 A、 B、 C、 D、10. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A、 B、 C、 D、10. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )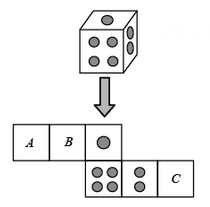 A、 代表
A、 代表 B、 代表
B、 代表  C、 代表
C、 代表  D、 代表
D、 代表 
二、填空题
-
11. 弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作 .已知 ,则 与 的大小关系是 .
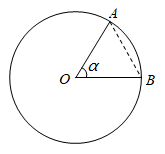 12. 平面直角坐标系中有点A(﹣2,4),则它到坐标原点的距离为 .13. 如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
12. 平面直角坐标系中有点A(﹣2,4),则它到坐标原点的距离为 .13. 如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则 (1)、x的值为;(2)、 的值为 .14. 度.15. 如图, 是两根木条,用 两根钉子钉在墙上,其中木条 可以绕点 转动,木条 被固定不动.这一生活现象用你学过的数学知识解释为 .
(1)、x的值为;(2)、 的值为 .14. 度.15. 如图, 是两根木条,用 两根钉子钉在墙上,其中木条 可以绕点 转动,木条 被固定不动.这一生活现象用你学过的数学知识解释为 .
三、作图题
-
16. 已知 和 都为正三角形,点B,C,D在同一直线上,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
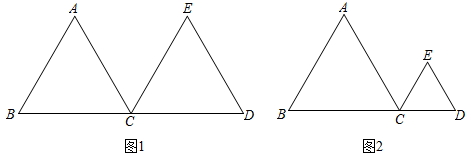 (1)、如图1,当 时,作 的中线 ;(2)、如图2,当 时,作 的中线 .17. 图1、图2都是4×4的正方形网格,每个小正方形的顶点叫做格点.△ABC的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)、如图1,当 时,作 的中线 ;(2)、如图2,当 时,作 的中线 .17. 图1、图2都是4×4的正方形网格,每个小正方形的顶点叫做格点.△ABC的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹. (1)、在图1中过点A作△ABC面积两等分的射线;(2)、在图2中过点A作所有将△ABC面积分成1∶2的两部分的射线.18. 如图,在△ABC中,BD是边AC上的高.请用尺规作图法,在BD上求作一点E,使得∠CED+∠ABD=90°.(保留作图痕迹,不写作法)
(1)、在图1中过点A作△ABC面积两等分的射线;(2)、在图2中过点A作所有将△ABC面积分成1∶2的两部分的射线.18. 如图,在△ABC中,BD是边AC上的高.请用尺规作图法,在BD上求作一点E,使得∠CED+∠ABD=90°.(保留作图痕迹,不写作法)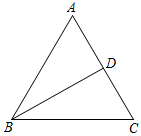
四、解答题
-
19. 如图,点C为线段 上一点,点B为 的中点,且 .求线段 的长.
 20. 如图,已知点C为AB上一点,AC=12 cm,CB= AC,点D,E分别为AC,AB的中点,求DE的长·
20. 如图,已知点C为AB上一点,AC=12 cm,CB= AC,点D,E分别为AC,AB的中点,求DE的长·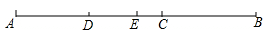 21. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
21. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 22. 如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
22. 如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 23. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
23. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.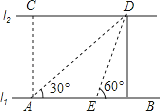
五、综合题
-
24.
用两种方法证明“三角形的外角和等于360°”.如图,
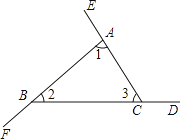
∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
请把证法1补充完整,并用不同的方法完成证法2.
(1)、证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
(2)、证法225. 如图,点C是线段AB的中点,D是线段AB的五等分点,若CD=6cm, (1)、求线段AB的长.(2)、若AE=DE,求线段EC的长.26. 一个几何体及它的表面展开图如图所示.(几何体的上、下底面均为梯形)
(1)、求线段AB的长.(2)、若AE=DE,求线段EC的长.26. 一个几何体及它的表面展开图如图所示.(几何体的上、下底面均为梯形) (1)、写出这个几何体的名称;(2)、计算这个几何体的侧面积和左视图的面积.27. 如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)、写出这个几何体的名称;(2)、计算这个几何体的侧面积和左视图的面积.27. 如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题: (1)、面“学”的对面是面什么?(2)、图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
(1)、面“学”的对面是面什么?(2)、图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.

