备考2022年中考数学一轮复习（湘教版）专题27 一次函数及其图像与性质

试卷更新日期：2021-09-20 类型：一轮复习

进入出卷网下载

一、单选题

1. 若一次函数 $y = k x + b$ 的图象如图所示，则下列说法正确的是（）

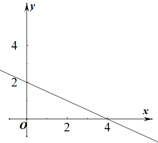A、 $k > 0$ B、 $b = 2$ C、y随x的增大而增大 D、 $x = 3$ 时， $y = 0$

查看试题解析
2. 小风在1000米中长跑训练时，已跑路程x（米）与所用时间t（秒）之间的函数图象如图所示，下列说法错误的是（）

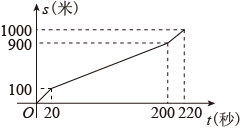A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒

查看试题解析
3. 在平面直角坐标系中，若将一次函数 $y = 2 x + m - 1$ 的图象向左平移3个单位后，得到个正比例函数的图象，则m的值为（）

A、-5 B、5 C、-6 D、6

查看试题解析
4. 一次函数y＝mx﹣m（m为常数且m≠0），若y随x增大而增大，则它的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限

查看试题解析
5. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，那么a、c满足（）

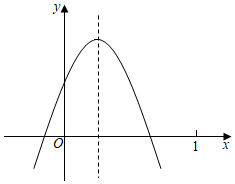A、a＞0，c＞0 B、a＞0，c＜0 C、a＜0，c＞0 D、a＜0，c＜0

查看试题解析
6. 在平面直角坐标系中，一次函数的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 将直线 $y = - x + 1$ 向左平移 $m$ （ $m > 0$ ）个单位后，经过点(1，−3)，则 $m$ 的值为.

查看试题解析
8. 若 $2 x + y = 1$ ，且 $0 < y < 1$ ，则 $x$ 的取值范围为.

查看试题解析
9. 已知函数 $y = k x$ 经过二、四象限，且函数不经过 $(- 1 ， 1)$ ，请写出一个符合条件的函数解析式．

查看试题解析
10. 直线y＝kx+b的图象如图所示，则代数式2k﹣b的值为 .

查看试题解析
11. 函数 $y = - x + 3$ 的图象向下平移3个单位，所得新图象的函数表达式是.

查看试题解析
12. 周末，步行爱好者甲、乙两人沿同一路线分别从A、B两地相向而行，匀速行进，甲先出发且先到达B地，甲、乙两人相距的路程y（单位：km）与甲出发的时间x（单位：h）之间的关系如图所示，则甲到达B地时，乙距离A地km.

查看试题解析
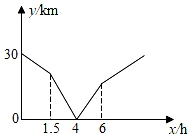13. 若一次函数 $y = k x - 1$ 的函数值y随自变量x的增大而增大，则实数k的取值范围是.

查看试题解析
14. 在平面直角坐标系内，一次函数y₁=k₁x+b₁与y₂=k₂x+b₂ 的图像如图所示，则关于x、y的方程组 ${\begin{matrix} y - k_{1} x = b_{1} \\ y - k_{2} x = b_{2} \end{matrix}$ 的解是.

查看试题解析

三、解答题

15. 已知直线y=kx﹣7经过点（2，﹣1），求关于x的不等式kx﹣7≥0的解集．

查看试题解析
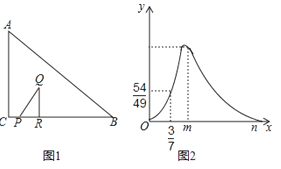
16.
Rt△ABC中，∠ACB=90°，BC=4，如图1，点P从C出发向点B运动，点R是射线PB上一点，PR=3CP，过点R作QR⊥BC，且QR=aCP，连接PQ，当P点到达B点时停止运动．设CP=x，△ABC与△PQR重合部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤ $\frac{3}{7}$ ， $\frac{3}{7}$ ＜x≤m，m＜x≤n时，函数的解析式不同）．
（1）a的值为；
（2）求出S关于x的函数关系式，并写出x的取值范围．

查看试题解析
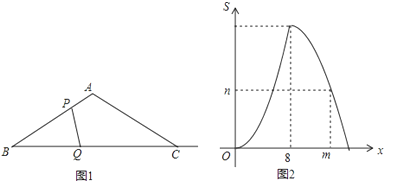
17.
如图1，在△ABC中，∠A=120°，AB=AC，点P、Q同时从点B出发，以相同的速度分别沿折线B→A→C、射线BC运动，连接PQ．当点P到达点C时，点P、Q同时停止运动．设BQ=x，△BPQ与△ABC重叠部分的面积为S．如图2是S关于x的函数图象（其中0≤x≤8，8＜x≤m，m＜x≤16时，函数的解析式不同）．
（1）求m的值。
（2）求S关于x的函数关系式，并写出x的取值范围；
（3）请直接写出△PCQ为等腰三角形时x的值．

查看试题解析
18. 已知函数y=（m²﹣m）x²+（m﹣1）x+m+1．若这个函数是一次函数，求m的值；

查看试题解析
19. 点A，B，C，D的坐标如图，求直线AB与直线CD的交点坐标．

查看试题解析
20.
如图，一次函数y=﹣ $\frac{4}{3}$ x+4的图象与x轴、y轴分别相交于点A、B．P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD=CP，连接PD．设BP=t．
t为何值时，点D恰好与点A重合？

查看试题解析

四、综合题

21. “黄金1号”玉米种子的价格为5元/kg。如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折。

(1)、填表：

购买量/kg

1

2

3

……

付款金额/元

……

(2)、直接写出付款金额关于购买量的函数解析式，并在给出的平面直角坐标系中画出函数图象。

查看试题解析
22. 我们知道： $| a | = {\begin{array}{l} a (a \geq 0) \\ - a (a < 0) \end{array}$ ，在函数 $y = | k x - 3 | + b$ 中，当 $x = 0$ 时， $y = - 1$ ，当 $x = 2$ 时， $y = - 4$ .

(1)、求这个函数的表达式；

(2)、在绘定的直角坐标中画出这个函数的图象，并写出一条这个函数具有的性质.

查看试题解析
23. 某列“复兴号”高铁从A站出发，以350km/h的速度向B站匀速行驶（途中不停靠），设行驶的时间为t（h），所对应的行驶路程为s（km）．

(1)、写出s关于t的函数表达式．

(2)、已知B站距离A站1400km，这列高铁在上午7点时离开A站．
①几点到达B站？

②若C站在A站和B站之间，且B ， C两站之间的距离为300km，借助所学的数学知识说明：列车途经C站时，已过上午10点．

查看试题解析
24. 如图，直线y＝﹣ $\frac{1}{2}$ x+3与坐标轴分别交于点A，B，与直线y＝x交于点C，Q为线段OA上的一个动点，连接CQ.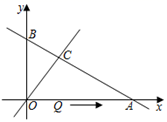

(1)、点C的坐标为；

(2)、当S_△ACQ：S_{四边形CQOB}＝2：7时，求直线CQ对应的函数关系式.

查看试题解析
25. 打车软件的出现很大程度上方便了我们的生活，其中“滴漓出行”是全球最大的站式多样化出行渠道，现了解到某市“滴滴快车”普通时段的最新收费标准见下表；

里程/千米

收费/元

2千米以下（含2千米）

11.4

2千米以上，每增加1千米

1.95

(1)、求“滴滴快车”的收费y（元）与行驶的里程数x（千米）之间的函数关系式；

(2)、上周一，李老师乘坐“滴滴快车”从家到学校的车费是15.3元，李老师家距离学校多少千米？已知王老师家距离学校1.8千米，求王老师乘坐“滴滴快车”从家到学校的车费.

查看试题解析
26. 在平面直角坐标系xOy中（如图），已知直线y＝﹣ $\frac{1}{2}$ x+2分别与x轴、y轴交于点A、B ，一个正比例函数的图象与这直线交于点C ，点C的横坐标是1．

(1)、求正比例函数的解析式；

(2)、将正比例函数的图象向上或向下平移，交直线y＝﹣ $\frac{1}{2}$ x+2于点D ，设平移后函数图象的截距为b ，如果交点D始终落在线段AB上，求b的取值范围．

查看试题解析

27. 函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索.画函数

y = - 2 | x |

的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数

y = - 2 | x | + 2

和

y = - 2 | x + 2 |

的图象如图所示.

x	…	﹣3	﹣2	﹣1	0	1	2	3	…
y	…	﹣6	﹣4	﹣2	0	﹣2	﹣4	﹣6	…

(1)、观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解折式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化.写出点A，B的坐标和函数

y = - 2 | x + 2 |

的对称轴.

(2)、探索思考：平移函数

y = - 2 | x |

的图象可以得到函数

y = - 2 | x | + 2

和

y = - 2 | x + 2 |

的图象，分别写出平移的方向和距离.

(3)、拓展应用：在所给的平面直角坐标系内画出函数

y = - 2 | x - 3 | + 1

的图象.若点

(x_{1} ， y_{1})

和

(x_{2} ， y_{2})

在该函数图象上，且

x_{2} > x_{1} > 3

，比较

y_{1}

，

y_{2}

的大小.

查看试题解析

28. 如图，直线l：y＝﹣ $\frac{1}{3}$ x+2与x轴、y轴分别交于A、B两点，动点M从点A以每秒1个单位的速度沿x轴向左移动.

(1)、求A、B两点的坐标；

(2)、将直线l向上平移4个单位后得到直线l'，交y轴于点C.求直线l′的函数表达式；

(3)、设点M的移动时间为t，当t为何值时，△COM≌△AOB，并求出此时点M的坐标.

查看试题解析
29. 如图，经过点 $B (1 ， 0)$ 的直线 $l_{1}$ 与直线 $l_{2} ： y = 2 x + 4$ 相交于点 $P (- 1 ， n)$ ．

(1)、请求 $n$ 的值；

(2)、求 $△ P A B$ 的面积．

查看试题解析
30. 如图，在平面直角坐标系中，直线y=x+4与y轴交于点A，与x轴交于点B，直线y=kx+b经过点A，且交x轴与点C(3，0).

(1)、求直线AC的函数表达式；

(2)、动点P在线段CB上由C向B匀速运动，到达点B后停止运动，运动速度为3个单位长度，过点P作PE⊥x轴，交直线AC于点E，过点E作直线GE∥x轴交y轴于点F，交直线AB于点G，设点P的运动时间为t(t＞0)秒.
①直接写出线段PE的长度(用含t的代数式表示)；

②当EG=1时，请直接写出t的值.

查看试题解析

里程/千米	收费/元
2千米以下（含2千米）	11.4
2千米以上，每增加1千米	1.95

购买量/kg	1	2	3	……
付款金额/元				……