备考2022年中考数学一轮复习（湘教版）专题14一元一次方程模型的建立及其应用
试卷更新日期：2021-09-20 类型：一轮复习
一、单选题
-
1. 已知某商店有两件进价不同的运动衫都卖了160元，其中一件盈利60%，另一件亏损20%，在这次买卖中这家商店（ ）A、不盈不亏 B、盈利20元 C、盈利10元 D、亏损20元2. 《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”：“粟率五十，粝米三十……”（粟指带壳的谷子，粝米指糙米），其意为：“50单位的粟，可换得30单位的粝米……”.问题：有3斗的粟（1斗＝10升），若按照此“粟米之法”，则可以换得粝米为（ ）A、1.8升 B、16升 C、18升 D、50升3. 端午节买粽子，每个肉粽比素粽多1元，购买10个肉粽和5个素粽共用去70元，设每个肉粽x元，则可列方程为（ ）A、 B、 C、 D、4. 某景点今年四月接待游客25万人次，五月接待游客60.5万人次，设该景点今年四月到五月接待游客人次的增长率为 （ ），则（ ）A、 B、 C、 D、5. 某超市正在热销一种商品，其标价为每件12元，打8折销售后每件可获利2元，该商品每件的进价为（ ）A、7.6元 B、7.7元 C、7.8元 D、7.9元6. 用150张铁皮做罐头盒，每张铁皮可制盒身15个或盒底45个，1个盒身与2个盒底配成一套罐头盒，为使制成的盒身与盒底恰好配套，可设用x张铁皮制盒底，则（ ）A、 B、 C、 D、7. 某校教师举行茶话会.若每桌坐10人，则空出一张桌子；若每桌坐8人，还有6人不能就坐.设该校准备的桌子数为 ，则可列方程为（ ）A、 B、 C、 D、8. 小涵在2020年某月的月历上圈出了三个数a，b，c，并求出了它们的和为30，则这三个数在月历中的排位位置不可能是（ ）A、
B、
C、
D、
二、填空题
-
9. 我国明代数学读本《算法统宗》一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托.如果1托为5尺，那么索长为尺.（其大意为：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺，则绳索长几尺.）10. 某企业有 两条加工相同原材料的生产线．在一天内， 生产线共加工 吨原材料，加工时间为 小时；在一天内， 生产线共加工 吨原材料，加工时间为 小时．第一天，该企业将5吨原材料分配到 两条生产线，两条生产线都在一天内完成了加工，且加工时间相同，则分配到 生产线的吨数与分配到 生产线的吨数的比为 ． 第二天开工前，该企业按第一天的分配结果分配了5吨原材料后，又给 生产线分配了 吨原材料，给 生产线分配了 吨原材料．若两条生产线都能在一天内加工完各自分配到的所有原材料，且加工时间相同，则 的值为 ．11. 某商场计划以每件75元的进价购进m件男士“T恤”衫．如果将这种男士“T恤”衫以每件100元售出，售完这批男士“T恤”衫获得的总利润是12. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托：折回索子却量竿，却比竿子短一托，”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺．则正确的方程是 ．13. 某校初一年级68名师生参加社会实践活动，计划租车前往，租车收费标准如下：
车型
大巴车
（最多可坐55人）
中巴车
（最多可坐39人）
小巴车
（最多可坐26人）
每车租金
（元∕天）
900
800
550
则租车一天的最低费用为元.
14. 我国古代问题：以绳测井，若将绳三折测之，绳多四尺，若将绳四折测之，绳多一尺，井深几何？这段话的意思是：用绳子量井深，把绳三折来量，井外余绳四尺，把绳四折来量，井外余绳一尺，井深几尺？则该问题的井深是尺.15. 小华到商店为班级购买跳绳和毽子两种体育用品，跳绳每个4元，毽子每个5元，两种体育用品共需购买22个，是否存在用90元钱完成这项购买任务的方案？（填“是”或“否”）．16. 某工厂生产一批零件，计划20天完成，若每天多生产5个，则16天完成且还多生产8个.设原计划每天生产x个，根据题意可列方程为.17. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足.问鸡兔各几何.”其大意是：“有若干只鸡和兔关在同一笼子里，它们一共有35个头，94条腿.问笼中的鸡和兔各有多少只？”若列一元一次方程 表示题中的数量关系，则方程中 表示的实际意义是.三、解答题
-
18. 运用方程或方程组解决实际问题：若干学生分若干支铅笔，如果每人5支，那么多余3支；如果每人7支，那么缺5支.试问有多少名学生？共有多少支铅笔？19. 一家商店在销售某种服装（每件的标价相同）时，按这种服装每件标价的8折销售10件的销售额，与按这种服装每件的标价降低30元销售11件的销售额相等.求这种服装每件的标价.20. 由于疫情防控的需要，学校开学第一周给某班配备了一定数量的口罩，若每个学生发5个，则多40个口罩，若每个学生发6个，则少12个口罩，请问该班有多少名学生？学校给该班准备了多少个口罩？21. 某农业公司原有葡萄园50亩，荷塘112亩，因葡萄热销，为了增加收入，该公司计划把部分荷塘改造为葡萄园，使葡萄园面积占荷塘面积的80%．求应把多少亩荷塘改造为葡萄园．22. 今年开学，由于疫情防控的需要，某学校统一购置口罩（1）班全体学生配备了一定数量的口罩，若每个学生发3个口罩，则多30个口罩，若给每个学生发5个口罩，则少50个口罩，请问该班有多少名学生？23. 岑溪市某个小区需要铺设天然气管道.现有甲、乙两个工程队共同铺设一段长为 的天然气管道.甲工程队每天铺设 ，乙工程队每天铺设 ，甲工程队先施工30天后，乙工程队也开始一起施工，乙工程队施工多少天后能完成这项工程？
四、综合题
-
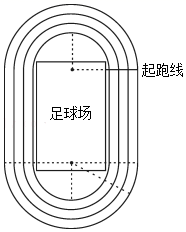
24. 为了美化环境，建设生态桂林，某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积.(1)、甲、乙两工程队每天各能完成多少平方米的绿化改造面积？(2)、该社区需要进行绿化改造的区域共有12000平方米，甲队每天的施工费用为600元，乙队每天的施工费用为400元，比较以下三种方案：①甲队单独完成；②乙队单独完成；③甲、乙两队全程合作完成.哪一种方案的施工费用最少？25. 据国际田联《田径场地设施标准手册》，400米标准跑道由两个平行的直道和两个半径相等的弯道组成，有8条跑道，每条跑道宽1.2米，直道长87米；跑道的弯道是半圆形，环形跑道第一圈（最内圈）弯道半径为35.00米到38.00米之间.
某校据国际田联标准和学校场地实际，建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长：
第一圈长：87×2＋2π（36＋1.2×0）≈400（米）；
第二圈长：87×2＋2π（36＋1.2×1）≈408（米）；
第三圈长：87×2＋2π（36＋1.2×2）≈415（米）；
……
请问：
(1)、第三圈半圆形弯道长比第一圈半圆形弯道长多多少米？小王计算的第八圈长是多少？(2)、小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车（均以所靠边线长计路程），在如图的起跑线同时出发，经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍，求他们的平均速度各是多少？（注：在同侧直道，过两人所在点的直线与跑道边线垂直时，称两人直道相遇）
26. 老师在黑板上写下了下图所示的等式，让同学自己出题，并作出答案．7+▢﹣5×〇＝38
请你解答下列两个同学所提出的问题．
(1)、甲同学提出的问题：当〇代表﹣2时，求▢所代表的有理数；(2)、乙同学提出的问题：若▢和〇所代表的有理数互为相反数，求〇所代表的有理数．27. 为了拉动内需，全国各地汽车购置税补贴活动在2009年正式开始，某经销商在政策出台前一个月共售出某品牌汽车的手动型和自动型共960台，政策出台后的第一个月售出这两种型号的汽车共1228台，其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%．(1)、在政策出台前一个月，销售的手动型和自动型汽车分别为多少台；(2)、若手动型汽车每台价格为8万元，自动型汽车每台价格为9万元．根据汽车补贴政策，政府按每台汽车价格的5%给购买汽车的用户补贴，问政策出台后的第一个月，政府对这1228台汽车用户共补贴了多少万元．28. 11月份脐橙和柚子进入销售旺季，某大型水果超市的脐橙和柚子这两种水果很受欢迎，脐橙售价12元/千克，柚子售价9元/千克.(1)、若第一周脐橙的销量比柚子的销量多200千克，要使这两种水果的销售总额达到6600元，则第一周应该销售脐橙多少千克?(2)、若该水果超市第一周按照（1）中脐橙和柚子的销量销售这两种水果，并决定第二周继续销售这两种水果.第二周脐橙售价降低了 元，销量比第一周增加了 .柚子的售价保持不变，销量比第一周增加了 ，结果这两种水果第二周的销售总额比第一周增加了 .求a的值.29. 元旦期间，家乐福超市搞促销活动，规定：购物不超过100元不给优惠；购物超过100元但不超过500元的，全部打9折；购物超过500元的，其中500元部分打9折，超过500元部分打8折.(1)、张老师第1次购得商品的总价（标价和）为300元，按活动规定实际付款多少元？(2)、张老师第2次购物，按活动规定实际付款490元，与没有促销相比，第2次购物节约了多少钱？(3)、若张老师将这两次购得的商品合为一次购买，是否更省钱？通过计算说出你的理由.30. 如图在长方形ABCD中，AB=12cm，BC=8cm，点P从A点出发，沿A→B→C→D路线运动，到D点停止；点Q从D点出发，沿D→C→B→A运动，到A点停止.若点P、点Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，用x（秒）表示运动时间.
(1)、求点P和点Q相遇时的x值.(2)、连接PQ，当PQ平分矩形ABCD的面积时，求运动时间x值.(3)、若点P、点Q运动到6秒时同时改变速度，点P的速度变为每秒3cm，点Q的速度为每秒1cm，求在整个运动过程中，点P、点Q在运动路线上相距路程为20cm时运动时间x值.