备考2022年中考数学一轮复习（湘教版）专题11 二次根式及其加减乘除

试卷更新日期：2021-09-20 类型：一轮复习

进入出卷网下载

一、单选题

1. 将 $\sqrt{\frac{45}{2}}$ 化为最简二次根式，其结果是（）

A、 $\sqrt{\frac{45}{2}}$ B、 $\frac{\sqrt{90}}{2}$ C、 $\frac{9 \sqrt{10}}{2}$ D、 $\frac{3 \sqrt{10}}{2}$

查看试题解析
2. 若二次根式 $\sqrt{x + 3}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \geq - 3$ B、 $x \geq 3$ C、 $x \leq - 3$ D、 $x > - 3$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{12} =$ 3 $\sqrt{2}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\frac{\sqrt{6}}{2} = \sqrt{3}$ D、（ $\sqrt{2}$ ）²＝2

查看试题解析
4. 计算： $(\frac{\sqrt{5} + 1}{2} - 1) \cdot \frac{\sqrt{5} + 1}{2} =$ （）

A、0 B、1 C、2 D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{2^{2}} = 2$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{2^{2}} = \pm 2$ D、 $\sqrt{{(- 2)}^{2}} = \pm 2$

查看试题解析
6. 下列计算中，正确的是（）

A、 $5 \sqrt{7} - 2 \sqrt{7} = 21$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{3} \times \sqrt{6} = 3 \sqrt{2}$ D、 $\sqrt{15} \div \sqrt{5} = 3$

查看试题解析
7. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ C、 $\sqrt{3} - \sqrt{2}$ ＝1 D、 $\sqrt{4} \div \sqrt{2}$ ＝2

查看试题解析
8. 下列计算正确的是（）

A、 $2 \sqrt{3} \div 3 \sqrt{2} = \frac{\sqrt{6}}{3}$ B、 $\sqrt{3} + \sqrt{5} = 2 \sqrt{2}$ C、 $3 \sqrt{5} - 3 = \sqrt{5}$ D、 $2 \sqrt{3} \times \sqrt{5} = \sqrt{15}$

查看试题解析
9. 估计 $\sqrt{39}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
10. 估计 $- \sqrt{7}$ 的值在（）

A、 $- 5$ 和 $- 4$ 之间 B、 $- 4$ 和 $- 3$ 之间 C、 $- 3$ 和 $- 2$ 之间 D、 $- 2$ 和 $- 1$ 之间

查看试题解析

二、填空题

11. 式子 $\sqrt{a + 2}$ 在实数范围内有意义，则a的取值范围是.

查看试题解析
12. 埃及胡夫金字塔是古代世界建筑奇迹之一，其底面是正方形，侧面是全等的等腰三角形，底面正方形的边长与侧面等腰三角形底边上的高的比值是 $\sqrt{5} - 1$ ，它介于整数n和n+1之间，则n的值是.

查看试题解析
13. 要使二次根式 $\sqrt{2 x - 4}$ 在实数范围内有意义，则x的取值范围是 .

查看试题解析
14. 已知 $y = \sqrt{x - 3} - \sqrt{3 - x} + 2$ ，则 $x^{y} =$ ．

查看试题解析
15. 若式子 $\sqrt{x + 3}$ 在实数范围内有意义，则x的取值范围．

查看试题解析
16. 已知： $- \sqrt{50} + \sqrt{\frac{1}{2}} = a \sqrt{2} + b \sqrt{2} = c \sqrt{2}$ ，则ab＋c的值可能是．

查看试题解析
17. 若a＜1，化简 $\sqrt{{(a - 1)}^{2}} - 1$ ＝.

查看试题解析
18. 已知，x、y为实数，且y＝ $\sqrt{x^{2} - 1}$ ﹣ $\sqrt{1 - x^{2}}$ +3，则x+y＝.

查看试题解析
19. 形如 $\sqrt{7 + 2 \sqrt{6}}$ 的根式叫做复合二次根式，对 $\sqrt{7 + 2 \sqrt{6}}$ 可进行如下化简： $\sqrt{7 + 2 \sqrt{6}}$ ＝ $\sqrt{{(\sqrt{6})}^{2} + 2 \sqrt{6} + 1} = \sqrt{{(\sqrt{6} + 1)}^{2}}$ ＝ $\sqrt{6}$ +1，利用上述方法化简： $\sqrt{10 - 2 \sqrt{21}} + \sqrt{4 - 2 \sqrt{3}} + 1$ ＝.

查看试题解析
20. 若a、b为有理数,且 $\sqrt{8} + \sqrt{18} + \sqrt{\frac{1}{8}} = a + b \sqrt{2}$ ,则a+b=

查看试题解析

三、计算题

21. 计算： ${(\sqrt{3} + 1)}^{2} - \sqrt{12} + 2 \sqrt{\frac{1}{3}}$ ．

查看试题解析
22. 计算： $(\sqrt{6} - \sqrt{2}) (\sqrt{2} + \sqrt{6}) - | \sqrt{6} - 3 | - {(- 1)}^{2021}$ .

查看试题解析
23. 计算： $\sqrt{8} \times \sqrt{6} - \frac{\sqrt{24}}{\sqrt{2}} + (\sqrt{3} + 1) (\sqrt{3} - 1)$ .

查看试题解析
24. 计算: $4 \sqrt{5} + \sqrt{45} - \sqrt{8} + 4 \sqrt{2}$

查看试题解析
25. 计算： $\sqrt{12} - \sqrt{18} + 3 \sqrt{\frac{1}{3}} + \sqrt{8}$ ．

查看试题解析
26. 计算 $| - \sqrt{2} | + {(\sqrt{2} - \frac{1}{2})}^{2} - {(\sqrt{2} + \frac{1}{2})}^{2}$ ．

查看试题解析
27. 计算： $\sqrt{3}$ （1﹣ $\sqrt{3}$ ）+ $\sqrt{12}$ +（ $\frac{1}{3}$ ）^﹣1 ．

查看试题解析
28. 化简：3a $\sqrt{12 a b}$ •（﹣ $\frac{2}{3} \sqrt{6 b}$ ）（a≥0，b≥0）

查看试题解析

四、解答题

29. 已知 $4 < a < 11$ ，化简： $\sqrt{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ .

查看试题解析
30. 若x，y都是实数，且y＝ $\sqrt{x - 4} + \sqrt{4 - x}$ +1，求 $\sqrt{x}$ +3y的值．

查看试题解析
31. （Ⅰ）已知方程① $\sqrt{x + 2016} + \sqrt{x - 2016} = \sqrt{2018}$
② $\sqrt{x - 2016} + \sqrt{x - 2017} + \sqrt{x - 2018} = 3$
请判断这两个方程是否有解？并说明理由；
（Ⅱ）已知 $\sqrt{3 x + 2016} + \sqrt{3 x - 2016} = 2016$ ，求 $\sqrt{3 x + 2016} - \sqrt{3 x - 2016}$ 的值．

查看试题解析
32. 观察下列各式：
$\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ； $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ； $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ；……
请你猜想：

(1)、 $\sqrt{4 + \frac{1}{6}} =$ ， $\sqrt{5 + \frac{1}{7}} =$ ；

(2)、计算(请写出推导过程)： $\sqrt{10 + \frac{1}{12}}$ ．

(3)、请你将猜想到的规律用含有自然数n（n≥1）的代数式表达出来．
．

查看试题解析
33. 如果二次根式 $\sqrt{3 a - 1}$ 与 $- 3 \sqrt{2}$ 能够合并，能否由此确定a=1？若能，请说明理由；不能，请举一个反例说明．

查看试题解析
34. 已知：x，y为实数，且 $y < \sqrt{x - 1} + \sqrt{1 - x} + 3$ ，化简： $| y - 3 | - \sqrt{y^{2} - 8 y + 16}$ ．

查看试题解析
35. 小东在学习了 $\frac{\sqrt{a}}{\sqrt{b}}$ = $\sqrt{\frac{a}{b}}$ 后，认为 $\sqrt{\frac{a}{b}}$ = $\frac{\sqrt{a}}{\sqrt{b}}$ 也成立，因此他认为一个化简过程： $\sqrt{\frac{- 20}{- 5}} = \frac{\sqrt{- 20}}{\sqrt{- 5}} = \frac{\sqrt{- 5} \cdot \sqrt{4}}{\sqrt{- 5}} = \sqrt{4} = 2$ 是正确的．你认为他的化简对吗？说说理由．

查看试题解析
36. 阅读下列材料，然后回答问题．在进行二次根式的化简运算时，我们有时会碰上形如 $\frac{2}{\sqrt{3} + 1}$ 的式子，其实我们还可以将其进一步简化： $\frac{2}{\sqrt{3} + 1}$ = $\frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)}$ = $\frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}}$ = $\sqrt{3}$ ﹣1．以上这种化简的步骤叫做分母有理化．
请用上面的方法化简： $\frac{1}{2 - \sqrt{3}}$ ．

查看试题解析
37. 阅读下面的问题：
$\frac{1}{\sqrt{2} + 1}$ = $\frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$ = $\sqrt{2}$ -1；
$\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})}$ = $\sqrt{3}$ - $\sqrt{2}$ ；
$\frac{1}{2 + \sqrt{3}}$ = $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})}$ =2﹣ $\sqrt{3}$
…
（1）求 $\frac{1}{\sqrt{8} + \sqrt{7}}$ 的值；
（2）已知m是正整数，求 $\frac{1}{\sqrt{m + 1} + \sqrt{m}}$ 的值；
（3）计算 $\frac{1}{\sqrt{2} + 1}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{2 + \sqrt{3}}$ …+ $\frac{1}{\sqrt{2015} + \sqrt{2014}}$ + $\frac{1}{\sqrt{2016} + \sqrt{2015}}$ ．

查看试题解析

五、综合题

38. 在一个边长为( $\sqrt{3} + \sqrt{2}$ ) cm的正方形内部挖去一个边长为( $\sqrt{3} - \sqrt{2}$ ) cm的正方形(如图)，求剩余部分(阴影)的面积.

查看试题解析
39. 已知实数a，b，c在数轴上的位置如图所示，化简|a|﹣ $\sqrt{{(a + c)}^{2}} + \sqrt{{(c - a)}^{2}} - \sqrt{b^{2}}$ ．

查看试题解析
40. 用※定义一种新运算：对于任意实数m和n ，规定 $m ※ n = m^{2} n - m n - 3 n$ ，如： $1 ※ 2 = 1^{2} \times 2 - 1 \times 2 - 3 \times 2 = - 6$ ．

(1)、求 $(- 2) ※ \sqrt{3}$ ；

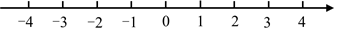(2)、若 $3 ※ m \geq - 6$ ，求m的取值范围，并在所给的数轴上表示出解集．

查看试题解析
41. 已知： $| m - 1 | + \sqrt{n + 2} = 0$ ，

(1)、求m ， n的值；

(2)、先化简，再求值： $m (m - 3 n) + {(m + 2 n)}^{2} - 4 n^{2}$ ．

查看试题解析
42. 观察下列等式：
第1个等式：a₁= $\frac{1}{1 + \sqrt{2}}$ = $\sqrt{2}$ ﹣1，
第2个等式：a₂= $\frac{1}{\sqrt{2} + \sqrt{3}}$ = $\sqrt{3}$ ﹣ $\sqrt{2}$ ，
第3个等式：a₃= $\frac{1}{\sqrt{3} + 2}$ =2﹣ $\sqrt{3}$ ，
第4个等式：a₄= $\frac{1}{2 + \sqrt{5}}$ = $\sqrt{5}$ ﹣2，
按上述规律，回答以下问题：

(1)、请写出第n个等式：a_n=；

(2)、a₁+a₂+a₃+…+a_n= ．

查看试题解析
43. 阅读下面问题：
$\frac{1}{\sqrt{2} + 1}$ = $\sqrt{2}$ ﹣1； $\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\sqrt{3}$ ﹣ $\sqrt{2}$ ； $\frac{1}{\sqrt{5} + 2}$ = $\sqrt{5}$ ﹣2．
猜测：（1） $\frac{1}{\sqrt{7} + \sqrt{6}}$ 的值；
（2） $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （n为正整数）的值．
（3）根据你的猜测计算：
$\frac{1}{1 + \sqrt{2}}$ + $\frac{1}{\sqrt{2} + \sqrt{3}}$ + $\frac{1}{\sqrt{3} + \sqrt{4}}$ +L+ $\frac{1}{\sqrt{98} + \sqrt{99}}$ + $\frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

查看试题解析
44. 阅读下面问题： $\frac{1}{\sqrt{2} + 1}$ = $\frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$ = $\sqrt{2}$ -1
$\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})}$ = $\sqrt{3}$ - $\sqrt{2}$
$\frac{1}{\sqrt{4} + \sqrt{3}}$ = $\frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})}$ = $\sqrt{4}$ - $\sqrt{3}$
…
（1）通过以上计算，观察规律，写出第n个式子．
（2）试求 $\frac{1}{1 + \sqrt{2}}$ + $\frac{1}{\sqrt{2} + \sqrt{3}}$ +...+ $\frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

查看试题解析
45. $\frac{1}{\sqrt{5} + \sqrt{4}}$ = $\frac{1 \times (\sqrt{5} - \sqrt{4})}{(\sqrt{5} + \sqrt{4}) (\sqrt{5} - \sqrt{4})}$ = $\frac{\sqrt{5} - \sqrt{4}}{{(\sqrt{5})}^{2} - {(\sqrt{4})}^{2}}$ = $\sqrt{5}$ - $\sqrt{4}$ = $\sqrt{5}$ ﹣2
$\frac{1}{\sqrt{6} + \sqrt{5}}$ = $\frac{1 \times (\sqrt{6} - \sqrt{5})}{(\sqrt{6} + \sqrt{5}) (\sqrt{6} - \sqrt{5})}$ = $\frac{\sqrt{6} - \sqrt{5}}{{(\sqrt{6})}^{2} - {(\sqrt{5})}^{2}}$ = $\sqrt{6}$ ﹣ $\sqrt{5}$
请回答下列问题：
（1）观察上面的解题过程．请直接写出结果． $\frac{1}{\sqrt{n} + \sqrt{n - 1}}$ 　
（2）利用上面提供的信息请化简：
$\frac{1}{\sqrt{2} + 1}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2007} + \sqrt{2008}}$ 的值．

查看试题解析
46. 王聪学习了二次根式性质公式 $\frac{\sqrt{a}}{\sqrt{b}}$ = $\sqrt{\frac{a}{b}}$ 后，他认为该公式逆过来 $\sqrt{\frac{a}{b}}$ = $\frac{\sqrt{a}}{\sqrt{b}}$ 也应该成立的，于是这样化简下面一题： $\sqrt{\frac{-27}{-3}}$ = $\frac{\sqrt{-27}}{\sqrt{-3}}$ = $\frac{\sqrt{(-3) \times 9}}{\sqrt{-3}}$ = $\sqrt{9}$ =3，你认为他的化简过程对吗？请说明理由.

查看试题解析
47. 阅读与计算：请阅读以下材料，并完成相应的任务．
斐波那契（约1170﹣1250）是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列）．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．
斐波那契数列中的第n个数可以用 $\frac{1}{\sqrt{5}}$ [( $\frac{1 + \sqrt{5}}{2}$ )ⁿ﹣( $\frac{1 - \sqrt{5}}{2}$ )ⁿ]表示（其中，n≥1）．这是用无理数表示有理数的一个范例．
任务：请根据以上材料，通过计算求出斐波那契数列中的第1个数和第2个数．

查看试题解析