北师版数学九年级上册《第四章 图形的相似》单元检测A卷
试卷更新日期:2021-09-20 类型:单元试卷
一、单选题
-
1. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( )
 A、 B、 C、 D、2. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )
A、 B、 C、 D、2. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1 , 则点A1的坐标为( )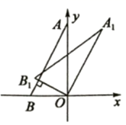 A、( ) B、( ) C、( ) D、( )3. 如图,在 中,若 ,则 ( )
A、( ) B、( ) C、( ) D、( )3. 如图,在 中,若 ,则 ( ) A、4 B、8 C、9 D、124. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、4 B、8 C、9 D、124. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )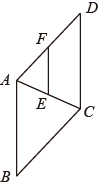 A、11 B、22 C、33 D、445. 如图,D、E、F分别是 各边中点,则以下说法错误的是( )
A、11 B、22 C、33 D、445. 如图,D、E、F分别是 各边中点,则以下说法错误的是( ) A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形6. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形6. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )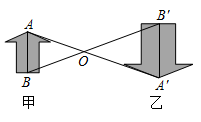 A、8 B、9 C、10 D、157. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )
A、8 B、9 C、10 D、157. 如图,平行四边形 的对角线 、 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( ) A、5.5 B、5 C、4 D、38. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )
A、5.5 B、5 C、4 D、38. 如图,已知 , , ,点E为射线 上一个动点,连接 ,将 沿 折叠,点B落在点 处,过点 作 的垂线,分别交 , 于M , N两点,当 为线段 的三等分点时, 的长为( )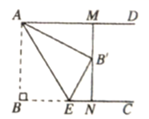 A、 B、 C、 或 D、 或9. 如图,平行四边形 的对角线 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )
A、 B、 C、 或 D、 或9. 如图,平行四边形 的对角线 相交于点E,点O为 的中点,连接 并延长,交 的延长线于点D,交 于点G,连接 、 ,若平行四边形 的面积为48,则 的面积为( )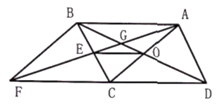 A、4 B、5 C、2 D、310. 如图,在平面直角坐标系中,点A在函数 的图象上,连结OA , 过点A作AB平行于x轴,点B在点A的右侧,连结OB交该函数图象于点C , 连结AC . 若 ,且 的面积为 ,则k的值为( )
A、4 B、5 C、2 D、310. 如图,在平面直角坐标系中,点A在函数 的图象上,连结OA , 过点A作AB平行于x轴,点B在点A的右侧,连结OB交该函数图象于点C , 连结AC . 若 ,且 的面积为 ,则k的值为( ) A、4 B、6 C、8 D、911. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )
A、4 B、6 C、8 D、911. 如图,在平行四边形 中,点E是边 上一点,且 , 交对角线 于点F,则 等于( )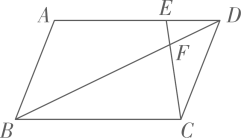 A、 B、 C、 D、12. 如图, 中, 为 边上的一点,过点 作 的平行线交 于点 ,连接 ,过点 作 的平行线交 于点 ,则下列结论中不一定成立的是( )
A、 B、 C、 D、12. 如图, 中, 为 边上的一点,过点 作 的平行线交 于点 ,连接 ,过点 作 的平行线交 于点 ,则下列结论中不一定成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.
 14. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .
14. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .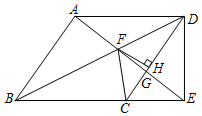 15. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .
15. 如图,在 中, , , ,点E在线段 上,且 ,D是线段 上的一点,连接 ,将四边形 沿直线 翻折,得到四边形 ,当点G恰好落在线段 上时, .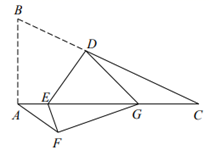 16. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.
16. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.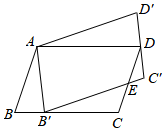 17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.
17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.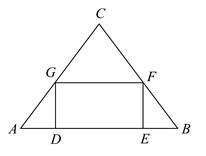 18. 如图, 中,点D为边BC的中点,连接AD,将 沿直线AD翻折至 所在平面内,得 ,连接 ,分别与边AB交于点E,与AD交于点O.若 , ,则AD的长为.
18. 如图, 中,点D为边BC的中点,连接AD,将 沿直线AD翻折至 所在平面内,得 ,连接 ,分别与边AB交于点E,与AD交于点O.若 , ,则AD的长为.
三、解答题
-
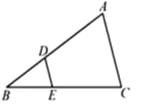
19. 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
 20. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
20. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.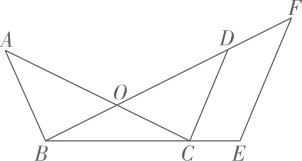 (1)、求证 ;(2)、若 ,求 的长.21. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
(1)、求证 ;(2)、若 ,求 的长.21. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.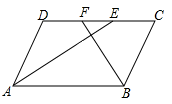
答案: .
(1)、探究:把“问题”中的条件“ ”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求 的值.22. 如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.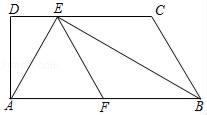
求证:
(1)、四边形BCEF是菱形;(2)、BE•AE=2AD•BC.23. 如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH. (1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.24. 如图,
(1)、求证:BE=CF;(2)、若AB=6,BE BC,求GH的长.24. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).