北师版数学九年级上册同步训练《4.7 相似三角形的性质》
试卷更新日期:2021-09-20 类型:同步测试
一、单选题
-
1. 已知 ,点C对应点F,若 , ,则 ( )A、 B、 C、 D、2. 如图△ABC∽△ACD,则下列式子中不成立的是( )
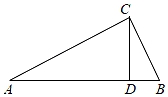 A、 = B、 = C、AC2=AD•AB D、 =3. 已知 ,相似比为 ,则 与 的面积比为( )A、 B、 C、 D、4. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A、 = B、 = C、AC2=AD•AB D、 =3. 已知 ,相似比为 ,则 与 的面积比为( )A、 B、 C、 D、4. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )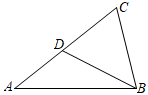 A、2 B、 C、 D、45. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( )
A、2 B、 C、 D、45. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( ) A、 B、 C、 D、6. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )A、30厘米、45厘米 B、40厘米、80厘米 C、80厘米、120厘米 D、90厘米、120厘米7. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE// BC,若AE: EC=1: 4,那么 的值为( )
A、 B、 C、 D、6. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )A、30厘米、45厘米 B、40厘米、80厘米 C、80厘米、120厘米 D、90厘米、120厘米7. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE// BC,若AE: EC=1: 4,那么 的值为( )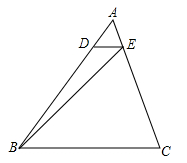 A、1∶16 B、1∶18 C、1∶20 D、1∶248. 如图,正方形ABCD的边长为2, , 线段MN的两端在CD,AD上滑动,当 与以D,M,N为顶点的三角形相似时,DM的长为( )
A、1∶16 B、1∶18 C、1∶20 D、1∶248. 如图,正方形ABCD的边长为2, , 线段MN的两端在CD,AD上滑动,当 与以D,M,N为顶点的三角形相似时,DM的长为( )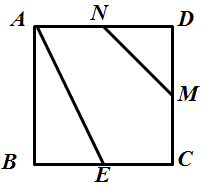 A、 B、 或 C、 D、 或9. 在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )A、没有发生变化 B、放大了10倍 C、放大了30倍 D、放大了100倍10. 两个相似三角形面积比是 ,其中一个三角形的周长为18,则另一个三角形的周长是( )A、12 B、12或24 C、27 D、12或27
A、 B、 或 C、 D、 或9. 在10倍的放大镜下看到的三角形与原三角形相比,三角形的周长( )A、没有发生变化 B、放大了10倍 C、放大了30倍 D、放大了100倍10. 两个相似三角形面积比是 ,其中一个三角形的周长为18,则另一个三角形的周长是( )A、12 B、12或24 C、27 D、12或27二、填空题
-
11. 已知△ABC的三边分别是5,6,7,则与它相似△ 的最短边为10,则△ 的周长是12. 如果两个相似三角形的面积比为4:9,较小三角形的周长为4,那么这两个三角形的周长和为.13. 如图, 平分 且 ,则当 时, .
 14. 如图所示,在矩形ABCD中, , ,点E在对角线BD上,且 ,连结AE并延长交DC于点F,则 .
14. 如图所示,在矩形ABCD中, , ,点E在对角线BD上,且 ,连结AE并延长交DC于点F,则 .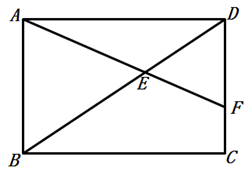 15. 如图, ,点 在 上, 与 交于点 , , ,则 的长为 .
15. 如图, ,点 在 上, 与 交于点 , , ,则 的长为 .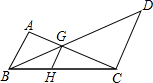 16. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
16. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .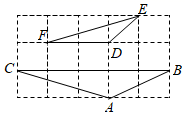
三、解答题
-
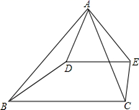
17. 如图,已知 , , ,求 的度数.
 18. 如图,在 中, , ,点 从点 出发沿 边想向点 以 的速度移动,点 从点 出发沿 边向点 以 的速度移动,如果 、 同时出发,经过几秒后 和 相似?
18. 如图,在 中, , ,点 从点 出发沿 边想向点 以 的速度移动,点 从点 出发沿 边向点 以 的速度移动,如果 、 同时出发,经过几秒后 和 相似?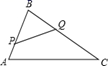 19. 如图,已知 的边BC=16,高AD=8,矩形EFGH的边FG在 的边BC上,顶点E、H分别在边AB、AC上,且FG=6,求边EF长
19. 如图,已知 的边BC=16,高AD=8,矩形EFGH的边FG在 的边BC上,顶点E、H分别在边AB、AC上,且FG=6,求边EF长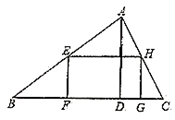 20. 已知:如图,△ADE∽△ABC,AB=10cm,AD=6cm,BC=12cm,∠A=56°,∠ADE=40°.求:∠ACB的度数及DE的长。
20. 已知:如图,△ADE∽△ABC,AB=10cm,AD=6cm,BC=12cm,∠A=56°,∠ADE=40°.求:∠ACB的度数及DE的长。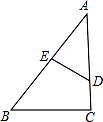 21. 已知:如图,在Rt△ABC中,∠C=90°,有一内接正方形DEFC,连接AF交DE于G,AC=15,BC=10,求EG的长.
21. 已知:如图,在Rt△ABC中,∠C=90°,有一内接正方形DEFC,连接AF交DE于G,AC=15,BC=10,求EG的长.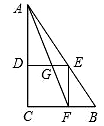 22. 如图,在△ABC中,∠B=90°,AB=6cm , BC=8cm . 点P从点A开始沿边AB向点B以每秒1cm的速度移动,点Q从点B开始沿边BC向点C以每秒2cm的速度移动,点P , Q分别从点A , B同时出发,且当一点到达终点时,另一点也停止运动.
22. 如图,在△ABC中,∠B=90°,AB=6cm , BC=8cm . 点P从点A开始沿边AB向点B以每秒1cm的速度移动,点Q从点B开始沿边BC向点C以每秒2cm的速度移动,点P , Q分别从点A , B同时出发,且当一点到达终点时,另一点也停止运动.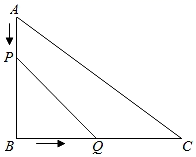 (1)、经过多少秒,可使PBQ的面积等于8cm2?(2)、经过多少秒,△ABC与△PBQ相似?(3)、线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(1)、经过多少秒,可使PBQ的面积等于8cm2?(2)、经过多少秒,△ABC与△PBQ相似?(3)、线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.