北师版数学九年级上册同步训练《4.6 利用相似三角形测高》
试卷更新日期:2021-09-20 类型:同步测试
一、单选题
-
1. 在某一时刻,测得一根高为 的竹杆的影长为 ,同时测得一栋楼的影长为 ,则这栋楼的高度为( )A、 B、 C、 D、2. 某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面 处重合,如图,测得 , ,则教学楼 的高是( )
 A、 B、 C、 D、3. 如图,小明(用 表示)站在旗杆(用 表示)的前方 处,某一时刻小明在地面上的影子 恰好与旗杆在地面上的影子 重合,若 , ,则旗杆 的高度为( )
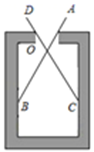
A、 B、 C、 D、3. 如图,小明(用 表示)站在旗杆(用 表示)的前方 处,某一时刻小明在地面上的影子 恰好与旗杆在地面上的影子 重合,若 , ,则旗杆 的高度为( ) A、 B、 C、 D、4. 如图是用卡钳测量容器内径的示意图,已知卡钳的四个端点 , , , 到支点 的距离满足 ,且 .现在只要测得卡钳外端 , 两个端点之间的距离,就可以计算出容器的内径 的大小。这种测量原理用到了( )
A、 B、 C、 D、4. 如图是用卡钳测量容器内径的示意图,已知卡钳的四个端点 , , , 到支点 的距离满足 ,且 .现在只要测得卡钳外端 , 两个端点之间的距离,就可以计算出容器的内径 的大小。这种测量原理用到了( ) A、图形的旋转 B、图形的平移 C、图形的轴对称 D、图形的相似5. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A、图形的旋转 B、图形的平移 C、图形的轴对称 D、图形的相似5. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( ) A、1.2m B、1.3m C、1.4m D、1.5m6. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A、1.2m B、1.3m C、1.4m D、1.5m6. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( ) A、60m B、40m C、30 D、20m7. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米,如图所示,然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
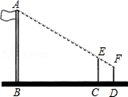
A、60m B、40m C、30 D、20m7. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米,如图所示,然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( ) A、10米 B、12米 C、15米 D、22.5米8. 如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( )
A、10米 B、12米 C、15米 D、22.5米8. 如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( ) A、5m B、6m C、7m D、8m9. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )
A、5m B、6m C、7m D、8m9. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )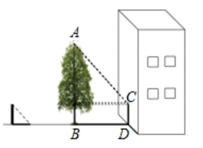 A、6.0m B、5.0m C、4.0m D、3.0m10. 已知:如图,小华在打羽毛球时,扣球要使球恰好能打过网,而且落在离网前4米的位置处,则球拍击球的高度h应为( )
A、6.0m B、5.0m C、4.0m D、3.0m10. 已知:如图,小华在打羽毛球时,扣球要使球恰好能打过网,而且落在离网前4米的位置处,则球拍击球的高度h应为( ) A、1.55m B、3.1m C、3.55m D、4m
A、1.55m B、3.1m C、3.55m D、4m二、填空题
-
11. 如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是.
 12. 在某一时刻,测得一根高为1.5 m的竹竿的影长为3 m,同时同地测得一栋楼的影长为60 m,则这栋楼的高度为m.13. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m.
12. 在某一时刻,测得一根高为1.5 m的竹竿的影长为3 m,同时同地测得一栋楼的影长为60 m,则这栋楼的高度为m.13. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m. 14.
14.如图,身高是1.6m的某同学直立于旗杆影子的顶端处,测得同一时刻该项同学和旗杆的影子长分别为1.2m和9m,则旗杆的高度为 m.
 15. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.
15. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.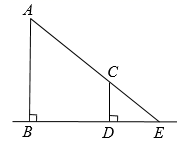 16. 如图,已知花丛中的电线杆AB上有一盏路灯A.灯光下,小明在点C处时,测得他的影长CD=3米,他沿BC方向行走到点E处时,CE=2米,测得他的影长EF=4米,如果小明的身高为1.6米,那么电线杆AB的高度等于米.
16. 如图,已知花丛中的电线杆AB上有一盏路灯A.灯光下,小明在点C处时,测得他的影长CD=3米,他沿BC方向行走到点E处时,CE=2米,测得他的影长EF=4米,如果小明的身高为1.6米,那么电线杆AB的高度等于米.
三、解答题
-
17. 在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,利用她所测数据,求旗杆的高.
 18. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.
18. 如图所示是测量河宽的示意图,AE与BC相交于点D,AB⊥BC于点B,CE⊥BC于点C,测得BD=150m,DC=75m,EC=60m,求河宽AB.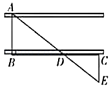 19. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板 来测量操场旗杆 的高度,他们通过调整测量位置,使斜边 与地面保持平行并使直角边 与旗杆顶点A在同一直线上,已知 米, 米,且测点D到地面的距离 米, ,到旗杆的水平距离 米,求旗杆 的高度.
19. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板 来测量操场旗杆 的高度,他们通过调整测量位置,使斜边 与地面保持平行并使直角边 与旗杆顶点A在同一直线上,已知 米, 米,且测点D到地面的距离 米, ,到旗杆的水平距离 米,求旗杆 的高度. 20. 如图,一天早上,明明正向着教学楼AB走去,他发现教学楼后面有一5G信号接收塔DC,可过了一会抬头一看:“怎么看不到接收塔了?”心里很是纳闷.经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离为30m,明明的眼睛距地面1.6m.当明明刚发现接收塔的顶部D被教学楼的顶部A挡住时,他与教学楼之间的距离为多少米?
20. 如图,一天早上,明明正向着教学楼AB走去,他发现教学楼后面有一5G信号接收塔DC,可过了一会抬头一看:“怎么看不到接收塔了?”心里很是纳闷.经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离为30m,明明的眼睛距地面1.6m.当明明刚发现接收塔的顶部D被教学楼的顶部A挡住时,他与教学楼之间的距离为多少米? 21. 如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
21. 如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.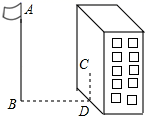 22. 青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.
22. 青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.