备考2022年中考数学一轮复习（湘教版）专题7 整式的乘法与乘法公式

试卷更新日期：2021-09-19 类型：一轮复习

进入出卷网下载

一、单选题

1. 若a＝ $\sqrt{3}$ ﹣2，则代数式a²+4a+6的值等（）

A、5 B、9 C、4 $\sqrt{3}$ ﹣3 D、4 $\sqrt{3}$ +5

查看试题解析
2. 下列计算正确的是（）

A、a³•a＝a³ B、（a²）³＝a⁵ C、4a•（﹣3ab）＝﹣12a²b D、（﹣3a²）³＝﹣9a⁶

查看试题解析
3. 下列运算正确的是（）

A、 $a^{- 2} \cdot a^{3} = a^{- 6}$ B、 ${(m - n)}^{2} = m^{2} - m n + n^{2}$ C、 ${(2 a^{3})}^{3} = 8 a^{6}$ D、 $(2 m + 1) (2 m - 1) = 4 m^{2} - 1$

查看试题解析
4. 计算 ${(a^{2})}^{3} \cdot a^{- 3}$ 的结果是（）

A、 $a^{2}$ B、 $a^{3}$ C、 $a^{5}$ D、 $a^{9}$

查看试题解析
5. 已知（a+b）²＝49，a²+b²＝25，则ab＝（）

A、24 B、48 C、12 D、2 $\sqrt{6}$

查看试题解析
6. 观察“赵爽弦图”（如图），若图中四个全等的直角三角形的两直角边分别为a ， b ， $a > b$ ，根据图中图形面积之间的关系及勾股定理，可直接得到等式（）

A、 $a (a - b) = a^{2} - a b$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

查看试题解析
7. 如果 $(x - 2) (x + 3) = x^{2} + p x + q$ ，那么 $p$ ， $q$ 的值分别是（）

A、 $p = 1$ ， $q = - 6$ B、 $p = - 1$ ， $q = - 6$ C、 $p = 5$ ， $q = 6$ D、 $p = - 5$ ， $q = - 6$

查看试题解析
8. 下列运算正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 $5 m^{2} \cdot m^{3} = 5 m^{5}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(m^{2})}^{3} = m^{5}$

查看试题解析
9. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $(a + b) (a - b) = a^{2} - b^{2}$

查看试题解析
10. 计算 ${(- 1.5)}^{2020} \times {(\frac{2}{3})}^{2021}$ 的结果是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $- \frac{2}{3}$

查看试题解析

二、填空题

11. 若x，y均为实数，43^x＝2021，47^y＝2021，则：

(1)、43^xy•47^xy＝（）^x+y；

(2)、 $\frac{1}{x} + \frac{1}{y}$ ＝.

查看试题解析
12. 已知a+b＝2，a﹣b＝3.则a²﹣b²的值为 .

查看试题解析
13. 若 $x$ 、 $y$ 满足 ${\begin{array}{l} x - 2 y = - 2 \\ x + 2 y = 3 \end{array}$ ，则代数式 $x^{2} - 4 y^{2}$ 的值为.

查看试题解析
14. 计算： ${(- 2)}^{2021} \cdot {(- \frac{1}{2})}^{2020} =$ .

查看试题解析
15. 在x²+（）+4=0的括号中添加一个关于 $x$ 的一次项，使方程有两个相等的实数根.

查看试题解析
16. 计算： ${(\sqrt{5} - 2)}^{2020} {(\sqrt{5} + 2)}^{2021}$ 的结果是．

查看试题解析
17. 若x＋2y－3＝0，则2^x·4^y的值为

查看试题解析
18. 已知： $a + b = 12, a b = 24$ ，则 $a^{2} + b^{2} =$ ．

查看试题解析
19. 计算 $1^{- 1} - {(\frac{1}{2})}^{2020} \times 2^{2021}$ 的结果是．

查看试题解析
20. 若ab＝1，a﹣b＝4，则 $\frac{b}{a} + \frac{a}{b}$ ＝.

查看试题解析

三、计算题

21. 先化简，再求值：x（x﹣2）+（x+1）² ，其中x=1．

查看试题解析
22. 先化简，再求值：2b²+(a+b)(a-b)-(a-b)² ，其中a=-3，b= $\frac{1}{2}$ 。

查看试题解析
23. 利用平方差公式可以进行简便计算：
例1：99×101=(100-1)(100+1)=100²-1²=10 000-1=9 999；

例2：39×410=39×41×10=(40-1)(40+1)×10=(40²-1²)×10=(1600-1)×10=1599×10=15 990.

请你参考上述算法，运用平方差公式简便计算：

(1)、 $\frac{19}{2} \times \frac{21}{2}$ ；

(2)、(2 019 $\sqrt{3}$ +2 019 $\sqrt{2}$ )( $\sqrt{3}$ - $\sqrt{2}$ ).

查看试题解析

四、解答题

24. 小明化简（2x+1）（2x﹣1）﹣x（x+5）的过程如图，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程．
解：原式=2x²﹣1﹣x（x+5）…①
=2x²﹣1﹣x²+5x…②
=x²+5x﹣1 …③

查看试题解析
25. 有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：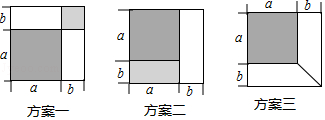

小明发现这三种方案都能验证公式：a²+2ab+b²＝（a+b）² ，

对于方案一，小明是这样验证的：

a²+ab+ab+b²＝a²+2ab+b²＝（a+b）²

请你根据方案二、方案三，写出公式的验证过程.

方案二：

方案三：

查看试题解析
26. 已知2^m＝a，8ⁿ＝b，m，n，是正整数，求2^3m+6n.

查看试题解析

五、综合题

27. 已知 $5 x^{2} - x - 1 = 0$ ，求代数式 $(3 x + 2) (3 x - 2) + x (x - 2)$ 的值．

查看试题解析
28. 已知：P＝3a（a+1）﹣（a+1）（a﹣1）

(1)、化简P；

(2)、若a为方程 $\frac{2}{3}$ x²+x﹣ $\frac{5}{3}$ ＝0的解，求P的值．

查看试题解析
29. 阅读下列材料解决问题：
材料一：完全平方数是指可以写成某个整数的平方的数，即其平方根为整数的数.例如， $9 = 3^{2} ， 9$ 是一个完全平方数.

材料二：对一个四位数，我们可以记为 $\bar{a b c d}$ ，即 $\bar{a b c d} = 1000 a + 100 b + 10 c + d$ ，若一个四位数的千位数字与百位数字相同，十位与个位数字相同，记为 $\bar{x x y y}$ ，我们称之为和谐四位数.

(1)、已知 $n$ 是使 $12 n$ 成为完全平方数的最小正整数，则 $n =$ ；

(2)、试证明任意一个和谐四位数都是 $11$ 的倍数；

(3)、若有和谐四位数 $\bar{x x y y}$ 是一个完全平方数，请求出符合条件的数.

查看试题解析
30. 有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：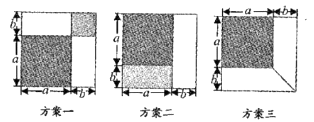

小明发现这三种方案都能验证公式：
a²+2ab+b²=（a+b）² ，
对于方案一，小明是这样验证的：
a²+ab+ab+b²=a²+2ab+b²=（a+b）²
请你根据方案二，方案三，写出公式的验证过程。

查看试题解析