备考2022年中考数学一轮复习（湘教版）专题6 整式及其加减法

试卷更新日期：2021-09-19 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列各式运算正确的是（）

A、2（a﹣1）=2a﹣1 B、a²b﹣ab²=0 C、a²+a²=2a² D、2a³﹣3a³=a³

查看试题解析
2. 若 $- 4 x^{m + 2} y^{4}$ 与 $2 x^{3} y^{n - 1}$ 为同类项，则m-n（）

A、-4 B、-3 C、-2 D、-1

查看试题解析
3. 下列运算结果正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 $7 a^{2} b - 4 a b^{2} = 3 a^{2} b$ C、 $x - (3 y - 2) = x - 3 y - 2$ D、 $- 2 (x + y) = - 2 x - 2 y$

查看试题解析
4. 单项式4ab²的系数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若A，B都是6次多项式，则A＋B是（）

A、6次多项式 B、12次多项式 C、次数不超过6次的多项式 D、次数不低于6次的多项式

查看试题解析
6. 下列说法中，正确的是（）

A、 $\frac{x^{2} y}{4}$ 不是整式 B、 $- \frac{2 a b^{2}}{3}$ 的系数是-2，次数是3 C、0是单项式，x＋2是多项式 D、多项式2x²-4y³＋1是五次三项式

查看试题解析
7. 在矩形ABCD内将两张边长分别为a和b(a>b)的正方形纸片
按图K2-4①②两种方式放置(图K2-4①②中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图①中阴影部分的面积为S₁ ，图②中阴影部分的面积为S₂.当AD-AB=2时， S₂-S₁的值为（）

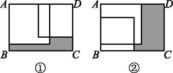A、2a B、2b C、2a-2b D、-2b

查看试题解析
8. 如图，两个面积分别为35，23的图形叠放在一起，两个阴影部分的面积分别为a，b(a>b)，则a-b的值为（）

A、6 B、8 C、9 D、12

查看试题解析
9. 把六张大小形状完全相同的小平行四边形卡片（如图）放在一个底面为平行四边形的盒子底部，两种放置方法如图2、图3所示，其中3中的重叠部分是平行四边形EFGH，若EH＝2GH，且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为（）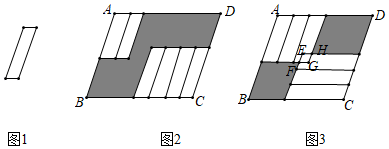

A、0.5 B、1 C、1.5 D、3

查看试题解析
10. 下列各式去括号正确的是（）

A、a-（b-c）=a-b-c B、a +（b-c）=a+b-c C、 $a^{2} - (a - b + c) = a^{2} - a - b + c$ D、 $a + 2 (3 a - 5) = a + 6 a - 5$

查看试题解析

二、填空题

11. 计算： $2 a^{2} - (a^{2} + 2) =$ .

查看试题解析
12. 已知单项式 $2 a^{4} b^{- 2 m + 7}$ 与 $3 a^{2 m} b^{n + 2}$ 是同类项，则m+n= ．

查看试题解析
13. 已知， $x - 3 = 2021$ ，则 ${(x - 3)}^{2} - 2021 (x - 3) + 1$ 的值为．

查看试题解析
14. 若多项式 $x y^{| m - n |} + (n - 2) x^{2} y^{2} + 1$ 是关于x，y的三次多项式，则 $m n =$ ．

查看试题解析
15. 单项式5mn²的次数为。

查看试题解析
16. 若 $a + 2 b = 8 ， 3 a + 4 b = 18$ ，则 $a + b$ 的值为.

查看试题解析
17. 如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉﹣﹣明白玉幻方．其背面有方框四行十六格，为四阶幻方（从1到16，一共十六个数目，它们的纵列、横行与两条对角线上4个数相加之和均为34）．小明探究后发现，这个四阶幻方中的数满足下面规律：在四阶幻方中，当数a ， b ， c ， d有如图1的位置关系时，均有a+b＝c+d＝17．如图2，已知此幻方中的一些数，则x的值为．

查看试题解析
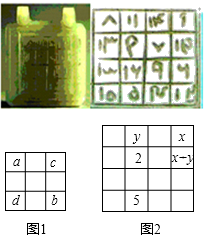18. 若m，n互为相反数，则3(m－n)－ $\frac{1}{2}$ (2m－10n)＝．

查看试题解析

三、计算题

19. 先化简，再求值： $5 x + 2 x^{2} - 6 x - x^{2} + 1$ ，其中 $x = 7$ .

查看试题解析
20. 若代数式(2x²＋ax－y＋6)－(2bx²－3x＋5y－1)的值与字母x的取值无关，求代数式 $\frac{1}{2}$ a²－2b＋4ab的值．

查看试题解析
21. 先化简，再求值：2x²–[3（– $\frac{1}{3}$ x²+ $\frac{2}{3}$ xy）–2y²]–2（x²–xy+2y²），其中x= $\frac{1}{2}$ ，y=–1.

查看试题解析

四、解答题

22. 三个队植树，第一队植树a棵，第二队植的树比第一队的2倍还多8棵，第三队植的树比第二队的一半少6棵，问三队共植树多少棵?并求当a=100时，三队共植树的棵数．

查看试题解析
23. 已知a，b为常数，且三个单项式4xy² ， axy^b ，－5xy相加得到的和仍是单项式，求a，b的值．

查看试题解析
24. 先化简再求值：4a²﹣3（2a﹣1）+6（a﹣2a²），其中a=﹣ $\frac{3}{2}$ ．

查看试题解析
25. 化简：2（3x²-2xy）-4（2x²-xy-1）

查看试题解析

五、综合题

26. 甲、乙两人各持一张分别写有整式 $A$ 、 $B$ 的卡片．已知整式 $C = a^{2} - 2 a - 5$ ，下面是甲、乙二人的对话：

甲：我的卡片上写着整式 $A = a^{2} - 4 a + 10$ ，加上整式 $C$ 后得到最简整式 $D$ ；

乙：我用最简整式 $B$ 加上整式 $C$ 后得到整式 $E = 6 a^{2} - 2 a + 8$ ．

根据以上信息，解决下列问题：

(1)、求整式D和B；

(2)、请判断整式 $D$ 和整式 $E$ 的大小，并说明理由．

查看试题解析
27. 如图，甲、乙两张卡片上均有一个系数为整数的多项式，其中乙中二次项系数因为被污染看不清楚．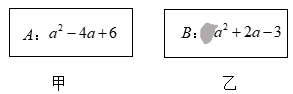

(1)、嘉嘉认为污染的数为-3，计算“ $A + B$ ”的结果；

(2)、若 $a = 3 + \sqrt{3}$ ，淇淇认为存在一个整数，可以使得“ $A - B$ ”的结果是整数，请你求出满足题意的被污染的这个数．

查看试题解析
28. 如图，约定：上方相邻两整式之和等于这两个整式下方箭头共同指向的整式．

(1)、求整式M；

(2)、请将整式N分解因式；

(3)、若 $P = - 4$ ，求x的值．

查看试题解析
29. 已知多项式M＝（2x²+3xy+2y）﹣2（x²+x+yx+1）.

(1)、当x＝1，y＝2，求M的值；

(2)、若多项式M与字母x的取值无关，求y的值.

查看试题解析