备考2022年中考数学一轮复习（湘教版）专题5 列代数式与代数式求值

试卷更新日期：2021-09-19 类型：一轮复习

进入出卷网下载

一、单选题

1. 定义一种新的运算：如果 $a \neq 0$ ．则有 $a ▲ b = a^{- 2} + a b + | - b |$ ，那么 $(- \frac{1}{2}) ▲ 2$ 的值是（）

A、-3 B、5 C、 $- \frac{3}{4}$ D、 $\frac{3}{2}$

查看试题解析
2. 如图，在平面直角坐标系中A（﹣1，1）B（﹣1，﹣2），C（3，﹣2），D（3，1），一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行，问第2021秒瓢虫在（）处．

A、（3，1） B、（﹣1，﹣2） C、（1，﹣2） D、（3，﹣2）

查看试题解析
3. 已知 $a_{1}$ 为实数﹐规定运算： $a_{2} = 1 - \frac{1}{a_{1}}$ ， $a_{3} = 1 - \frac{1}{a_{2}}$ ， $a_{4} = 1 - \frac{1}{a_{3}}$ ， $a_{5} = 1 - \frac{1}{a_{4}}$ ，……， $a_{n} = 1 - \frac{1}{a_{n - 1}}$ .按上述方法计算：当 $a_{1} = 3$ 时， $a_{2021}$ 的值等于（）

A、 $- \frac{2}{3}$ B、 $\frac{1}{3}$ C、 $- \frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 观察下列树枝分杈的规律图，若第n个图树枝数用 $Y_{n}$ 表示，则 $Y_{9} - Y_{4} =$ （）

A、 $15 \times 2^{4}$ B、 $31 \times 2^{4}$ C、 $33 \times 2^{4}$ D、 $63 \times 2^{4}$

查看试题解析
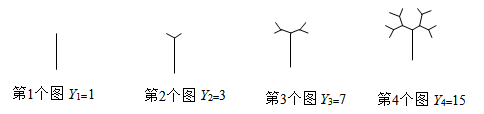5. 根据图中数字的规律，若第 $n$ 个图中的 $q = 143$ ，则 $p$ 的值为（）

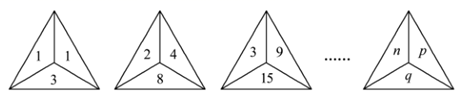A、100 B、121 C、144 D、169

查看试题解析
6. 将x克含糖10%的糖水与y克含糖30%的糖水混合，混合后的糖水含糖（）

A、20% B、 $\frac{x + y}{2}$ ×100% C、 $\frac{x + 3 y}{20}$ ×100% D、 $\frac{x + 3 y}{10 x + 10 y}$ ×100%

查看试题解析
7. 某地居民生活用水收费标准：每月用水量不超过17立方米，每立方米 $a$ 元；超过部分每立方米 $(a + 1.2)$ 元.该地区某用户上月用水量为20立方米，则应缴水费为（）

A、 $20 a$ 元 B、 $(20 a + 24)$ 元 C、 $(17 a + 3.6)$ 元 D、 $(20 a + 3.6)$ 元

查看试题解析
8. 某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（）

A、先打九五折，再打九五折 B、先提价 $50 %$ ，再打六折 C、先提价 $30 %$ ，再降价 $30 %$ D、先提价 $25 %$ ，再降价 $25 %$

查看试题解析
9. 若 $x = \sqrt{2} + 1$ ，则代数式 $x^{2} - 2 x + 2$ 的值为（）

A、7 B、4 C、3 D、 $3 - 2 \sqrt{2}$

查看试题解析
10. 已知x²﹣3x﹣12＝0，则代数式﹣3x²+9x+5的值是（）

A、31 B、﹣31 C、41 D、﹣41

查看试题解析

二、填空题

11. 若x²+x﹣1＝0，则3x﹣ $\frac{3}{x}$ ＝.

查看试题解析
12. 已知 $t^{2} - 3 t + 1 = 0$ ，则 $t + \frac{1}{t} =$ .

查看试题解析
13. 如图，在平面直角坐标系中，动点P从原点O出发，水平向左平移1个单位长度，再竖直向下平移1个单位长度得到点 $P_{1} (- 1 ， - 1)$ ；接着水平向右平移2个单位长度，再竖直向上平移2个单位长度得到点 $P_{2}$ ；接着水平向左平移3个单位长度，再竖直向下平移3个单位长度得到点 $P_{3}$ ；接着水平向右平移4个单位长度，再竖直向上平移4个单位长度得到点 $P_{4}$ ，…，按此作法进行下去，则点 $P_{2021}$ 的坐标为.

查看试题解析
14. 按一定规律排列的一列数依次为 $\frac{2}{3}$ ， $\frac{1}{4}$ ， $\frac{2}{15}$ ， $\frac{1}{12}$ ， $\frac{2}{35}$ ，…，按此规律排列下去，这列数中的第n个数是.

查看试题解析
15. y与x之间的函数关系可记为y＝f（x）.例如：函数y＝x²可记为f（x）＝x².若对于自变量取值范围内的任意一个x，都有f（﹣x）＝f（x），则f（x）是偶函数；若对于自变量取值范围内的任意一个x，都有f（﹣x）＝﹣f（x），则f（x）是奇函数.例如：f（x）＝x²是偶函数，f（x） $= \frac{1}{x}$ 是奇函数.若f（x）＝ax²+（a﹣5）x+1是偶函数，则实数a＝.

查看试题解析
16. 已知非零实数x，y满足 $y = \frac{x}{x + 1}$ ，则 $\frac{x - y + 3 x y}{x y}$ 的值等于.

查看试题解析
17. 幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1~9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a的值为．

查看试题解析

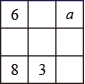
三、解答题

18. 对于实数a、b，定义运算“ $\oplus$ ”如下： $a \oplus b = a^{2} - b$ ．若 $(x + 1) \oplus (x - 2) = 8$ ，求x的值．

查看试题解析
19. 已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{5}$ ，且2x+y+3z≠0，求 $\frac{x + 2 y - 3 z}{2 x + y + 3 z}$ 的值.

查看试题解析
20. 为了节约用水，某市自来水公司采取以下收费方法：每户每月用水不超过10吨，每吨收费 1.5 元；每户每月用水超过10吨，超过的部分按每吨3元收费现在已知小明家2月份用水x吨 (x＞10），请用代数式表示小明家2月份应交水费多少元？如果 x=16 ，那么小明家2月份应交水费多少元？

查看试题解析
21. 如图，自左向右，水平摆放一组小球，按照以下规律排列，如：红球，黄球，绿球，红球，黄球，绿球，…，嘉琪依次在小球上标上数字1，2，3，4，5，6，…
尝试：左数第三个黄球上标的数字是多少？

应用：若某个小球上标的数字是101，则这个小球的颜色是什么？它左边共有多少个与它颜色相同的小球？

发现：试用含n的代数式表示左边第n个黄球所标的数字．

查看试题解析
22. 直角坐标系第二象限内的点P（x²+2x，3）与另一点Q（x+2，y）关于原点对称，试求x+2y的值．

查看试题解析

四、综合题

23. 观察以下等式：
第1个等式： $\frac{1}{3} \times (1 + \frac{2}{1}) = 2 - \frac{1}{1}$

第2个等式： $\frac{3}{4} \times (1 + \frac{2}{2}) = 2 - \frac{1}{2}$

第3个等式： $\frac{5}{5} \times (1 + \frac{2}{3}) = 2 - \frac{1}{3}$

第4个等式： $\frac{7}{6} \times (1 + \frac{2}{4}) = 2 - \frac{1}{4}$

第5个等式： $\frac{9}{7} \times (1 + \frac{2}{5}) = 2 - \frac{1}{5}$

······

按照以上规律．解决下列问题：

(1)、写出第6个等式；

(2)、写出你猜想的第n个等式： ▲ (用含 $n$ 的等式表示)，并证明．

查看试题解析
24. 对有序数对 $(m ， n)$ 规定运算： $f (m ， n) = m^{2} - n + 2$ ．例如， $f (3 ， 2) = 3^{2} - 2 + 2 = 9$ ．

(1)、求 $f (- 2 ， 5)$ 的结果；

(2)、若 $f (m ， 1) = - 2 m$ ，求 $m$ 的值．

查看试题解析
25. 老师在黑板上出示了下面的5个未计算完的有理数．
${(- 1)}^{2}$ ， $| - 2 |$ ， $- (- 4)$ ， $\frac{- 2.5 + 0.5}{2}$ ， $- 3^{3}$

(1)、求这5个数的和，并直接写出这5个数的中位数．

(2)、在这5个数中，最大的数是m ，最小的数是n ．求 ${(7 m + n)}^{2020} - m n$ 的值．

查看试题解析
26. 观察下列等式：
① $\frac{3^{2} - 1^{2}}{4} = 1 + 1$ ；② $\frac{4^{2} - 2^{2}}{4} = 1 + 2$ ；③ $\frac{5^{2} - 3^{2}}{4} = 1 + 3$ ；④ $\frac{6^{2} - 4^{2}}{4} = 1 + 4$ ；⑤ $\frac{7^{2} - 5^{2}}{4} = 1 + 5$ ……

(1)、请按以上规律写出第⑥个等式；

(2)、猜想并写出第n个等式 ▲ ；并证明猜想的正确性．

(3)、利用上述规律，计算： $\frac{3^{2} - 1^{2} - 4}{4} + \frac{4^{2} - 2^{2} - 4}{4} + \frac{5^{2} - 3^{2} - 4}{4} + \dots + \frac{2021^{2} - 2019^{2} - 4}{4}$ = ．

查看试题解析
27. 观察下列等式：
第1个等式：2²－2×1＝1²＋1；

第2个等式：3²－2×2＝2²＋1；

第3个等式：4²－2×3＝3²＋1；…；

(1)、请直接写出第4个等式：

(2)、根据上述等式的排列规律，猜想第n（n是正整数）个等式，并运用所学知识说明猜想的正确性．

查看试题解析
28. 解密数学魔术：魔术师请观众心想一个数a，然后将这个数按以下步骤操作：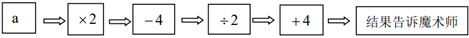

魔术师能立刻说出观众想的那个数．

(1)、如果小明想的数是-1，那么她告诉魔术师的结果应该是；

(2)、如果小明想了一个数计算后，告诉魔术师结果为42，那么魔术师立刻说出小明想的那个数是；

(3)、观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数．请通过计算说明这个魔术的奥妙．

查看试题解析
29. 嘉嘉和琪琪用图中的 $A$ 、 $B$ 、 $C$ 、 $D$ 四张带有运算的卡片，做一个“我说你算”的数学游戏，规则如下：嘉嘉说一个数，并对这个数按这四张带有运算的卡片排列出一个运算顺序，然后琪琪根据这个运算顺序列式计算，并说出计算结果．例如，嘉嘉说2，对2按 $A \to B \to C \to D$ 的顺序运算，则琪琪列式计算得： ${[(2 + 3) \times (- 3) - 2]}^{2} = {(- 15 - 2)}^{2} = {(- 17)}^{2} = 289$ ．

(1)、嘉落说-2，对-2按 $C \to A \to D \to B$ 的顺序运算，请列式并计算结果；

(2)、嘉嘉说 $x$ ，对 $x$ 按 $C \to B \to D \to A$ 的顺序运算后，琪琪得到的数恰好等于12，求 $x$ ．

查看试题解析
30. 观察下列等式：
① $\frac{1}{1} + \frac{1}{2} - \frac{1}{2} = \frac{1}{1}$ ；② $\frac{1}{3} + \frac{1}{4} - \frac{1}{12} = \frac{1}{2}$ ；③ $\frac{1}{5} + \frac{1}{6} - \frac{1}{30} = \frac{1}{3}$ ；……

(1)、请按以上规律写出第④个等式：；

(2)、猜想并写出第 $n$ 个等式：；

(3)、请证明猜想的正确性．

查看试题解析