湘教版数学九年级上册《 第4章 锐角三角函数》单元检测B卷
试卷更新日期:2021-09-18 类型:单元试卷
一、单选题
-
1. 如图,拦水坝的横断面为梯形ABCD.其中 , , ,斜坡AB长8m.则斜坡CD的长为( )
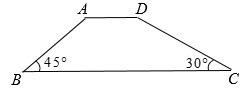 A、 B、 C、 D、2. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A、 B、 C、 D、2. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )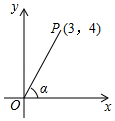 A、 B、 C、 D、3. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a64. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、 B、 C、 D、3. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a64. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )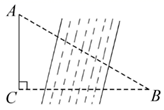 A、 B、 C、 D、5. 如图,在矩形 中, , , 是 的中点,将 沿直线 翻折,点落 在点 处,连结 ,则 的长为( )
A、 B、 C、 D、5. 如图,在矩形 中, , , 是 的中点,将 沿直线 翻折,点落 在点 处,连结 ,则 的长为( ) A、 B、 C、 D、6. 如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是( )
A、 B、 C、 D、6. 如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是( ) A、3 B、 C、 D、7. 如图, 底边 上的高为 , 底边 上的高为 ,则有( )
A、3 B、 C、 D、7. 如图, 底边 上的高为 , 底边 上的高为 ,则有( )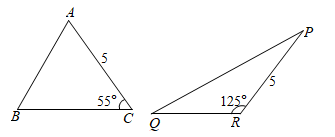 A、 B、 C、 D、以上都有可能8. 如图,在矩形 中,连接 ,将 沿对角线 折叠得到 交 于点O , 恰好平分 ,若 ,则点O到 的距离为( )
A、 B、 C、 D、以上都有可能8. 如图,在矩形 中,连接 ,将 沿对角线 折叠得到 交 于点O , 恰好平分 ,若 ,则点O到 的距离为( ) A、 B、2 C、 D、39. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )
A、 B、2 C、 D、39. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )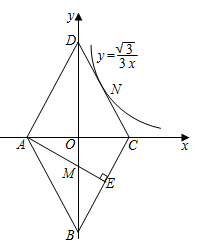 A、 B、 C、 D、10. 如图, 的顶点是正方形网格的格点,则 的值为( )
A、 B、 C、 D、10. 如图, 的顶点是正方形网格的格点,则 的值为( )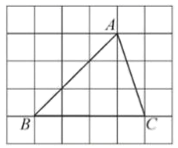 A、 B、 C、 D、11. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )
A、 B、 C、 D、11. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )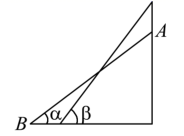 A、1米 B、1.5米 C、2米 D、2.5米12. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
A、1米 B、1.5米 C、2米 D、2.5米12. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).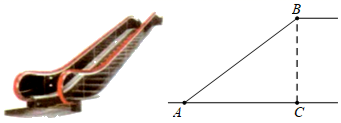 A、7.5米 B、8米 C、9米 D、10米
A、7.5米 B、8米 C、9米 D、10米二、填空题
-
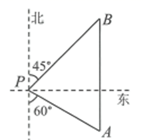
13. 如图,一艘轮船位于灯塔P的南偏东 方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东 方向上的B处,此时B处与灯塔P的距离为海里(结果保留根号).
 14. 计算: .15. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
14. 计算: .15. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.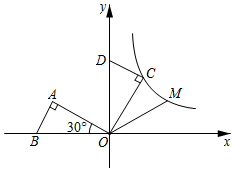 16. 如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 ,则tan∠DEC的值是.
16. 如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 ,则tan∠DEC的值是.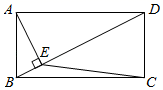 17. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.18. 如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为 ,从A处沿水平方向飞行至B处需 ,同时在地面C处分别测得A处的仰角为 ,B处的仰角为 .则这架无人机的飞行高度大约是 ( ,结果保留整数)
17. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.18. 如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为 ,从A处沿水平方向飞行至B处需 ,同时在地面C处分别测得A处的仰角为 ,B处的仰角为 .则这架无人机的飞行高度大约是 ( ,结果保留整数)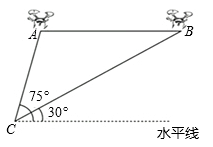
三、解答题
-
19. 计算: .20. 计算:21. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , )
 22. 张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据: )
22. 张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据: ) 23. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )
23. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )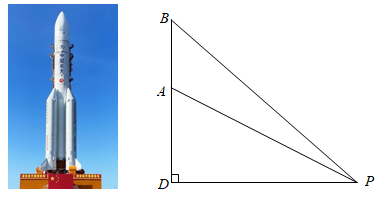 24. 如图,在一座山的前方有一栋住宅,已知山高 m,楼高 m,某天上午9时太阳光线从山顶点 处照射到住宅的点 外.在点 处测得点 的俯角 ,上午10时太阳光线从山顶点 处照射到住宅点 处,在点 处测得点 的俯角 ,已知每层楼的高度为3m, m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( )
24. 如图,在一座山的前方有一栋住宅,已知山高 m,楼高 m,某天上午9时太阳光线从山顶点 处照射到住宅的点 外.在点 处测得点 的俯角 ,上午10时太阳光线从山顶点 处照射到住宅点 处,在点 处测得点 的俯角 ,已知每层楼的高度为3m, m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( )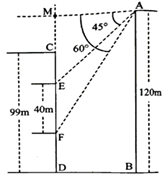 25. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内).
25. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内). (1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).
(1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).