湘教版数学九年级上册《第4章 锐角三角函数》单元检测A卷
试卷更新日期:2021-09-18 类型:单元试卷
一、单选题
-
1. 的值等于( )A、 B、 C、1 D、22. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( )
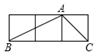 A、 B、 C、 D、3. 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A、 B、 C、 D、3. 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )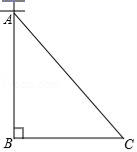 A、 B、 C、6cos50° D、4. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A、 B、 C、6cos50° D、4. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )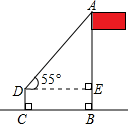 A、tan55°= B、tan55°= C、sin55°= D、cos55°=5. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )
A、tan55°= B、tan55°= C、sin55°= D、cos55°=5. 比萨斜塔是意大利的著名建筑,其示意图如图所示.设塔顶中心点为点B,塔身中心线 与垂直中心线 的夹角为 ,过点B向垂直中心线 引垂线,垂足为点D.通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是( )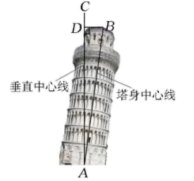 A、 B、 C、 D、6. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、 B、 C、 D、6. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )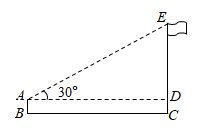 A、 B、 C、 D、7. 某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度.
A、 B、 C、 D、7. 某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度.①当 时, 小于3.3米的车辆均可以通过该闸口;②当 时, 等于2.9米的车辆不可以通过该闸口;③当 时, 等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为( )
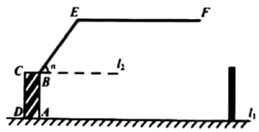 A、0个 B、1个 C、2个 D、3个8. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )
A、0个 B、1个 C、2个 D、3个8. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )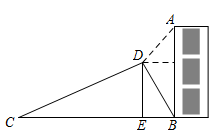 A、69.2米 B、73.1米 C、80.0米 D、85.7米9. 如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米, ,则缆车从A点到达B点,上升的高度(BC的长)为( )
A、69.2米 B、73.1米 C、80.0米 D、85.7米9. 如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米, ,则缆车从A点到达B点,上升的高度(BC的长)为( )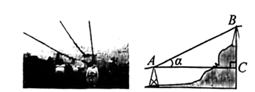 A、 米 B、 米 C、 米 D、 米10. 在 中, ,若 ,则 的长是( )A、 B、 C、60 D、8011. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据: ≈1.732)( )
A、 米 B、 米 C、 米 D、 米10. 在 中, ,若 ,则 的长是( )A、 B、 C、60 D、8011. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据: ≈1.732)( ) A、136.6米 B、86.7米 C、186.7米 D、86.6米12. 如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)( )
A、136.6米 B、86.7米 C、186.7米 D、86.6米12. 如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)( )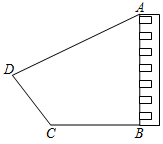 A、76.9m B、82.1m C、94.8m D、112.6m
A、76.9m B、82.1m C、94.8m D、112.6m二、填空题
-
13. 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.
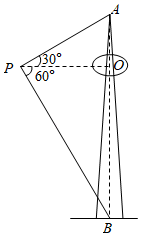 14. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据: , )
14. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据: , ) 15. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).
15. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).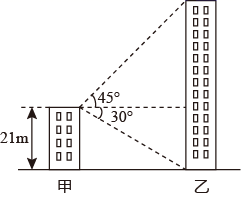 16. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
16. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )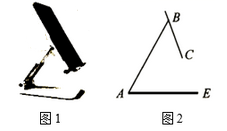 17. 如图,海中有一个小岛 ,一艘轮船由西向东航行,在 点测得小岛 在北偏东 方向上;航行 到达 点,这时测得小岛 在北偏东 方向上.小岛 到航线 的距离是 ( ,结果用四舍五入法精确到0.1).
17. 如图,海中有一个小岛 ,一艘轮船由西向东航行,在 点测得小岛 在北偏东 方向上;航行 到达 点,这时测得小岛 在北偏东 方向上.小岛 到航线 的距离是 ( ,结果用四舍五入法精确到0.1).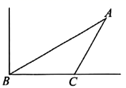 18. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A , D , B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据 , , )
18. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A , D , B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据 , , )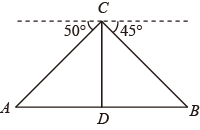
三、解答题
-
19. 计算:20. 计算:(π﹣1)0+| ﹣2|﹣( )﹣1+tan60°.21. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , )
 22. 今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为 ,站在同一队列B处的小刚测得国旗C处的仰角为 ,已知小明目高 米,距旗杆 的距离为15.8米,小刚目高 米,距小明24.2米,求国旗的宽度 是多少米?(最后结果保留一位小数)(参考数据: )
22. 今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为 ,站在同一队列B处的小刚测得国旗C处的仰角为 ,已知小明目高 米,距旗杆 的距离为15.8米,小刚目高 米,距小明24.2米,求国旗的宽度 是多少米?(最后结果保留一位小数)(参考数据: )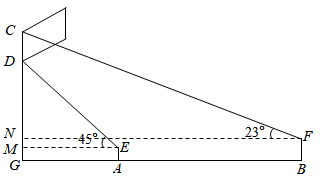 23. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , )
23. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , ) 24. 某海域有一小岛P,在以P为圆心,半径r为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东 的方向上,当海监船行驶 海里后到达B处,此时观测小岛P位于B处北偏东 方向上.
24. 某海域有一小岛P,在以P为圆心,半径r为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东 的方向上,当海监船行驶 海里后到达B处,此时观测小岛P位于B处北偏东 方向上. (1)、求A,P之间的距离AP;(2)、若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)、求A,P之间的距离AP;(2)、若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .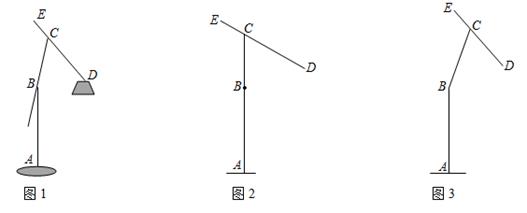 (1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )
(1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )