湘教版数学九年级上册同步训练《4.2 正切》
试卷更新日期:2021-09-18 类型:同步测试
一、单选题
-
1. 如图, 的顶点位于正方形网格的格点上,若 ,则满足条件的 是( )A、
 B、
B、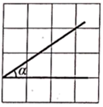 C、
C、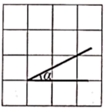 D、
D、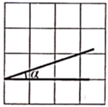
-
2. 已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )A、10cos50° B、10sin50° C、10tan50° D、10cot50°
-
3. 若锐角α满足cosα< 且tanα< ,则α的范围是( )A、30°<α<45° B、45°<α<60° C、60°<α<90° D、30°<α<60°
-
4. 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c , 下列等式中成立的是( )A、 B、 C、 D、
-
5. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则tanB的值是( )A、 B、 C、 D、
-
6. 在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,下列结论正确的是( )A、b=a•sinA B、b=a•tanA C、c=a•sinA D、a=c•cosB
-
7. 在 中, ,则下列结论正确的是( )A、 B、 C、 D、
-
8. 在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )A、不变 B、扩大5倍 C、缩小5倍 D、不能确定
-
9. 如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
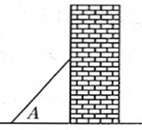 A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关
A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关 -
10. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( )
 A、 B、75sin80° C、 D、
A、 B、75sin80° C、 D、
二、填空题
-
11. 如图所示的正方形网格中有 ,则 的值为 .

-
12. 如图, 的顶点都是正方形网格中的格点,则 .

-
13. 已知一斜坡的坡比为1:2,坡角为 ,那么 .
-
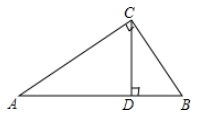
14. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则tan∠BCD的值是.
-
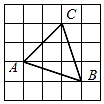
15. 如图,点A,B,C为正方形网格中的3个格点,则tan∠ACB=.
-
16. 若三个锐角 满足 ,则 由小到大的顺序为.
三、解答题
-
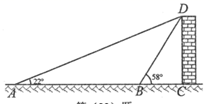
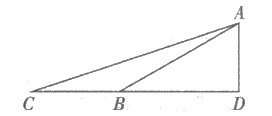
17. 如图,为测量建筑物 的高度,在A处测得建筑物顶部D处的仰角为 ,再向建筑物 前进 到达B处,测得建筑物顶部D处的仰角为 (A , B , C在同一条直线上),求建筑物 的高度(结果取整数).参考数据: .
-
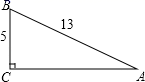
18. 如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.
-
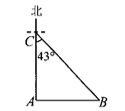
19. 如图,海面上 , 两岛分别位于 岛的正东和正北方向.一艘船从 岛出发以16海里 的速度向正北方向航行2小吋到达 岛,此吋测得 岛在 岛的南偏东 .求 , 两岛之间的距离.(结果精确到0.1海里)(参考数据: , , )
-
20. 步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡 改造成 .已知原坡角 ,改造后的斜坡 的坡度为 , 米,求原斜坡 的长.(精确到0.1米,参考数据: )
-
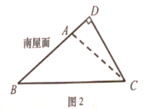
21. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)
(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)

-
22. 某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出符合题意的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)