湘教版数学九年级上册同步训练《4.1 正弦和余弦》
试卷更新日期:2021-09-18 类型:同步测试
一、单选题
-
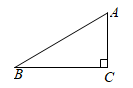
1. 在Rt△ABC中,已知∠C=90°,AC=4,BC=3,则cosA等于( )A、 B、 C、 D、2. 如图,在 中, , , ,则 ( )
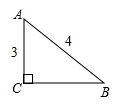 A、 B、 C、 D、3. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、4. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、5. 如图,一把梯子靠在垂直水平地面的墙上,梯子 的长是3米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离BC为( )
A、 B、 C、 D、3. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、4. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、5. 如图,一把梯子靠在垂直水平地面的墙上,梯子 的长是3米.若梯子与地面的夹角为 ,则梯子顶端到地面的距离BC为( )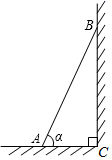 A、 米 B、 米 C、 米 D、 米6. 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
A、 米 B、 米 C、 米 D、 米6. 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )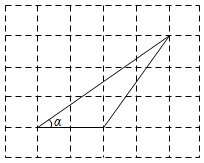 A、 B、 C、 D、7. 在 中, , ,则( )
A、 B、 C、 D、7. 在 中, , ,则( )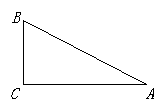 A、 B、 C、 D、8. 如图,在 中, 是斜边 上的高, ,则下列比值中等于 的是( )
A、 B、 C、 D、8. 如图,在 中, 是斜边 上的高, ,则下列比值中等于 的是( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( ) A、 B、 C、 D、10. 在 中, ,垂足为D,则下列比值中不等于 的是( )
A、 B、 C、 D、10. 在 中, ,垂足为D,则下列比值中不等于 的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sinB的值是
 12. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D , AB=8,AC=6,则cos∠DCB= .
12. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D , AB=8,AC=6,则cos∠DCB= .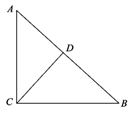 13. 如图,在平面直角坐标系中有一点 ,那么 与 轴的正半轴的夹角 的余弦值为 .
13. 如图,在平面直角坐标系中有一点 ,那么 与 轴的正半轴的夹角 的余弦值为 .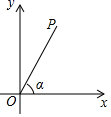 14. 在 中, , 是高,且 ,则 .15. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .
14. 在 中, , 是高,且 ,则 .15. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .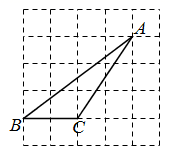 16. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .
16. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .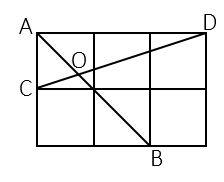
三、解答题
-
17. 在 中, , , , 的对边分别为a,b,c, , ,求c的值.18. 在△ABC中,∠C=90°,BC=24cm,cosA= ,求这个三角形的周长.
19. 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.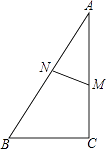 20. 如图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上,不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②,其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN,我们把∠ANB叫做倾斜角,根据以上数据,判断倾斜角能小于30°吗?请说明理由.
20. 如图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上,不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②,其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN,我们把∠ANB叫做倾斜角,根据以上数据,判断倾斜角能小于30°吗?请说明理由. 21. △ABC,∠C=90°,BC=3,AB=5,求sinA,cosA的值.22. 阅读材料,回答问题:
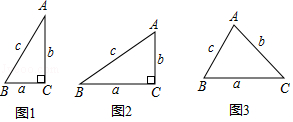
21. △ABC,∠C=90°,BC=3,AB=5,求sinA,cosA的值.22. 阅读材料,回答问题:小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= ,AB=c=2,那么 = =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着 = = 的关系.
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)、如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“ = = ”的关系是否成立?(2)、完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ = = ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).