湘教版数学九年级上册第一次月考试题模拟A卷(第一、二章综合)
试卷更新日期:2021-09-18 类型:月考试卷
一、单选题
-
1. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、2. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为 的函数图象.根据这个函数的图象,下列说法正确的是( )
 A、图象与 轴没有交点 B、当 时 C、图象与 轴的交点是 D、 随 的增大而减小3. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且4. 在同一直角坐标系中,函数 与 的大致图象是( )
A、图象与 轴没有交点 B、当 时 C、图象与 轴的交点是 D、 随 的增大而减小3. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且4. 在同一直角坐标系中,函数 与 的大致图象是( )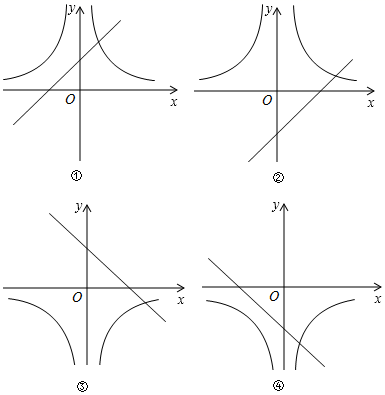 A、①② B、②③ C、②④ D、③④5. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、6. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、47. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或8. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或9. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、10. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A、①② B、②③ C、②④ D、③④5. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、6. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、47. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或8. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或9. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、10. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )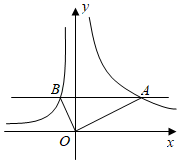 A、5t B、 C、 D、511. 随着互联网技术的发展,我国快递业务量逐年增加,据统计从2018年到2020年,我国快递业务量由507亿件增加到833.6亿件,设我国从2018年到2020年快递业务量的年平均增长率为x , 则可列方程为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )
A、5t B、 C、 D、511. 随着互联网技术的发展,我国快递业务量逐年增加,据统计从2018年到2020年,我国快递业务量由507亿件增加到833.6亿件,设我国从2018年到2020年快递业务量的年平均增长率为x , 则可列方程为( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )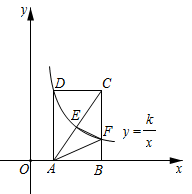 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
13. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
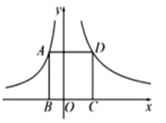 14. 若m,n是一元二次方程 的两个实数根,则 的值为.15. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.
14. 若m,n是一元二次方程 的两个实数根,则 的值为.15. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.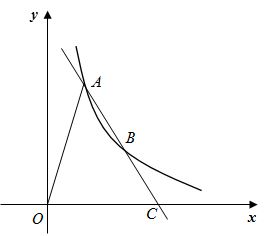 16. 对于实数a,b,定义运算“*“,a*b= 例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1 , x2是一元二次方程x2﹣8x+16=0的两个根,则x1*x2=.17. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
16. 对于实数a,b,定义运算“*“,a*b= 例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1 , x2是一元二次方程x2﹣8x+16=0的两个根,则x1*x2=.17. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
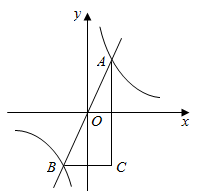 18. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
18. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
三、解答题
-
19. 解方程: .20. 用配方法求一元二次方程 的实数根.21. 如图,一次函数 (k1、b为常数,k1≠0)的图象与反比例函数 的图象交于点A(m,8)与点B(4,2).
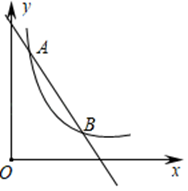
①求一次函数与反比例函数的解析式.
②根据图象说明,当x为何值时, .
22. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根分别为 、 ,且 ,求 的值.23. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点. (1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.24. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?25. 阅读理解:
(1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.24. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?25. 阅读理解:材料一:若三个非零实数x , y , z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实教x , y , z构成“和谐三数组”.
材料二:若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为 , ,则有 , .
问题解决:
(1)、请你写出三个能构成“和谐三数组”的实数;(2)、若 , 是关于x的方程ax2+bx +c= 0 (a , b , c均不为0)的两根, 是关于x的方程bx+c=0(b , c均不为0)的解.求证:x1 ,x2 , x3可以构成“和谐三数组”;(3)、若A(m , y1) ,B(m + 1,y2) ,C(m+3,y3)三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.