湘教版数学九年级上册第一次月考试题模拟B卷(第一、二章综合)
试卷更新日期:2021-09-18 类型:月考试卷
一、单选题
-
1. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)2. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
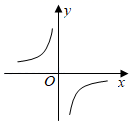 A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为 ,下面所列方程正确的是( )A、 B、 C、 D、4. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、96. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为 ,下面所列方程正确的是( )A、 B、 C、 D、4. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、96. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )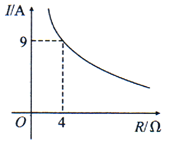 A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A7. 关于 的方程 有实数根,则k的取值范围是( )A、 且 B、 且 C、 D、8. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )
A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A7. 关于 的方程 有实数根,则k的取值范围是( )A、 且 B、 且 C、 D、8. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )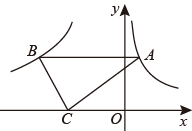 A、-6 B、-8 C、-10 D、-129. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定10. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当 时,x的取值范围是( )
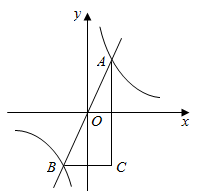
A、-6 B、-8 C、-10 D、-129. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定10. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,点B的横坐标为2,当 时,x的取值范围是( )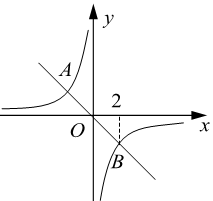 A、 或 B、 或 C、 或 D、 或11. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根12. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )
A、 或 B、 或 C、 或 D、 或11. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根12. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )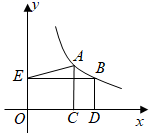 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
13. 关于x的方程 有两个实数根 .且 .则 .14. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ;
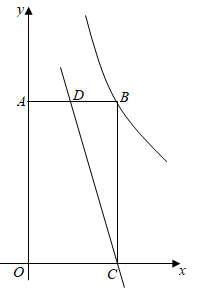
 15. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
15. 如图,正比例函数 与函数 的图象交于A,B两点, 轴, 轴,则 .
 16. 已知关于 的一元二次方程 ,有下列结论:
16. 已知关于 的一元二次方程 ,有下列结论:①当 时,方程有两个不相等的实根;
②当 时,方程不可能有两个异号的实根;
③当 时,方程的两个实根不可能都小于1;
④当 时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为 .
17. 如图,点A是反比例函数 图象上一点, 轴于点C且与反比例函数 的图象交于点B , ,连接OA , OB , 若 的面积为6,则 .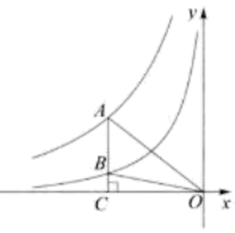 18. 如图, 是等腰三角形, 过原点O,底边 轴双曲线 过A,B两点,过点C作 轴交双曲线于点D,若 ,则k的值是.
18. 如图, 是等腰三角形, 过原点O,底边 轴双曲线 过A,B两点,过点C作 轴交双曲线于点D,若 ,则k的值是.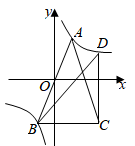
三、解答题
-
19. 用配方法解方程: .20. 解方程21. 如图,在平面直角坐标系中.四边形 为矩形,点 、 分别在 轴和 轴的正半轴上,点 为 的中点已知实数 ,一次函数 的图象经过点 、 ,反比例函数 的图象经过点 ,求 的值.
 22. 已知 , 是一元二次方程 的两个实数根.(1)、求k的取值范围;(2)、是否存在实数k,使得等式 成立?如果存在,请求出k的值,如果不存在,请说明理由.23. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象
22. 已知 , 是一元二次方程 的两个实数根.(1)、求k的取值范围;(2)、是否存在实数k,使得等式 成立?如果存在,请求出k的值,如果不存在,请说明理由.23. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象①列表:下表是 与 的几组对应值,其中 ▲ ;
…
-4
-3
-2
0
1
2
…
…
-1
=2
-3
3
2
…
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
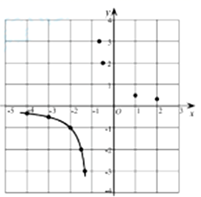 (2)、探究函数性质
(2)、探究函数性质判断下列说法是否正确。
①函数值 随 的增大而减小:
②函数图象关于原点对称:
③函数图象与直线 没有交点.
24. 如图:在平面直角坐标系中,菱形 的顶点D在y轴上,A,C两点的坐标分别为 ,直线 与双曲线: 交于C, 两点.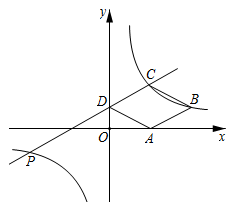 (1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.25. 重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.(1)、求每份“堂食”小面和“生食”小面的价格分别是多少元?(2)、该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份,为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低 .统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加 ,这两种小面的总销售额在4月的基础上增加 .求a的值.
(1)、求双曲线 的函数关系式及m的值;(2)、判断点B是否在双曲线上,并说明理由;(3)、当 时,请直接写出x的取值范围.25. 重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.(1)、求每份“堂食”小面和“生食”小面的价格分别是多少元?(2)、该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份,为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低 .统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加 ,这两种小面的总销售额在4月的基础上增加 .求a的值.