江苏省镇江市2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-18 类型:期中考试
一、填空题
-
1. 如图,△ABC≌△A'B'C',其中∠A=35°,∠C=25°,则∠B'=.
 2. 如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=2,则点P到OB的距离为.
2. 如图,已知OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=2,则点P到OB的距离为. 3. 直角三角形的两条直角边长为6,8,那么斜边上的中线长是 .4. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF.
3. 直角三角形的两条直角边长为6,8,那么斜边上的中线长是 .4. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF. 5. 如图,以直角三角形一边向外作正方形,其中两个正方形的面积为100和64,则正方形A的面积为
5. 如图,以直角三角形一边向外作正方形,其中两个正方形的面积为100和64,则正方形A的面积为 6. 等腰三角形的一个角是50°,则它的顶角等于°.7. 如图,将一张长方形纸片按如图所示折叠,如果∠1=55°,那么∠2=°.
6. 等腰三角形的一个角是50°,则它的顶角等于°.7. 如图,将一张长方形纸片按如图所示折叠,如果∠1=55°,那么∠2=°.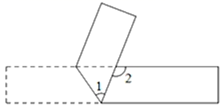 8. 如图,在 中, 的垂直平分线 交 于点 ,连接 .若 , ,则 的周长是.
8. 如图,在 中, 的垂直平分线 交 于点 ,连接 .若 , ,则 的周长是. 9. 如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=5,DC=7,DE=16,则FG=.
9. 如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=5,DC=7,DE=16,则FG=. 10. 如图,在 中, 平分 , 于点 ,已知 的面积为 ,则阴影部分的面积为 .
10. 如图,在 中, 平分 , 于点 ,已知 的面积为 ,则阴影部分的面积为 . 11. 如图,等腰△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E,BD的垂直平分线交AB于点F,并且恰好经过点C,则∠A=°.
11. 如图,等腰△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E,BD的垂直平分线交AB于点F,并且恰好经过点C,则∠A=°. 12. 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的高,点B关于AD的对称点为B',点A关于BC的对称点为A',连接A'B'并延长,交AC于点E,若AB=3,AC=4,则线段CE的长为.
12. 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的高,点B关于AD的对称点为B',点A关于BC的对称点为A',连接A'B'并延长,交AC于点E,若AB=3,AC=4,则线段CE的长为.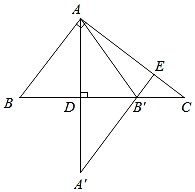
二、单选题
-
13. 下面四个手机的图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 14. 小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
14. 小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( ) A、21:10 B、10:21 C、10:51 D、12:0115. 下列四组线段中,不能作为直角三角形三边长度的是( )A、3,4,5 B、8,15,17 C、1.5,2,2.5 D、16. 到三角形三边的距离相等的点是( )A、三角形三内角平分线的交点; B、三角形三边中线的交点; C、三角形三边高的交点; D、三角形三边中垂线的交点。17. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( )
A、21:10 B、10:21 C、10:51 D、12:0115. 下列四组线段中,不能作为直角三角形三边长度的是( )A、3,4,5 B、8,15,17 C、1.5,2,2.5 D、16. 到三角形三边的距离相等的点是( )A、三角形三内角平分线的交点; B、三角形三边中线的交点; C、三角形三边高的交点; D、三角形三边中垂线的交点。17. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( ) A、1个 B、2个 C、3个 D、4个18. 如图,在△ABC中,∠ACB=90°,Rt△ABC≌Rt△AB'C',且∠ABC=∠CAB',连接BC',并取BC'的中点D,则下列四种说法:
A、1个 B、2个 C、3个 D、4个18. 如图,在△ABC中,∠ACB=90°,Rt△ABC≌Rt△AB'C',且∠ABC=∠CAB',连接BC',并取BC'的中点D,则下列四种说法:①AC'//BC;
②△ACC'是等腰直角三角形;
③AD平分∠CAB';
④AD⊥CB'.
其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个三、解答题
-
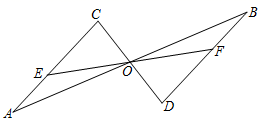
19. 如图,AB、CD相交于点O,△AOC≌△BOD,点E在AC上,EO的延长线交BD于点F.求证:O是EF的中点.
 20. 如图所示,每个小正方形的边长为1,△ABC的顶点都在小正方形的顶点处.
20. 如图所示,每个小正方形的边长为1,△ABC的顶点都在小正方形的顶点处.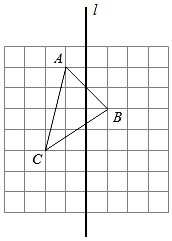 (1)、画出△ABC关于直线l对称的△A'B'C';(2)、直接写出△A'B'C'的面积等于 ;(3)、在直线l上求作一点P,使PA+PC的长度最小,并写出这个最小值为 .21. 如图,点B、F、C、E在同一直线上,AB⊥BE,垂足为B,DE⊥BE,垂足为E,AC、DF相交于点G,且AC=DF,BF=CE.
(1)、画出△ABC关于直线l对称的△A'B'C';(2)、直接写出△A'B'C'的面积等于 ;(3)、在直线l上求作一点P,使PA+PC的长度最小,并写出这个最小值为 .21. 如图,点B、F、C、E在同一直线上,AB⊥BE,垂足为B,DE⊥BE,垂足为E,AC、DF相交于点G,且AC=DF,BF=CE. (1)、求证:△ABC≌△DEF;(2)、若∠A=65°,则∠DGC=°.22. 如图,AB=AC,BD=CD.
(1)、求证:△ABC≌△DEF;(2)、若∠A=65°,则∠DGC=°.22. 如图,AB=AC,BD=CD. (1)、求证:△ABD≌△ACD;(2)、连接BC,求证:AD⊥BC.23. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .
(1)、求证:△ABD≌△ACD;(2)、连接BC,求证:AD⊥BC.23. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .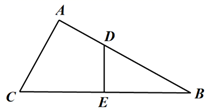
 (1)、求证: ;(2)、若 , ,求 的长.24. 如图,在△ABC中,∠ACB=90°,AC=BC=AD.
(1)、求证: ;(2)、若 , ,求 的长.24. 如图,在△ABC中,∠ACB=90°,AC=BC=AD. (1)、作△ACD的高AE,点E为垂足(要求:尺规作图,不写作法,保留作图痕迹);(2)、在射线CD上找一点P,使△PCB与(1)中所作的△ACE全等(要求:尺规作图,不写作法,保留作图痕迹).并证明你所作出的△PCB与△ACE全等.25. 如图,点E在等边△ABC的边AB所在直线上,以EC为一边作等边△ECF,顶点E、C、F顺时针排序.
(1)、作△ACD的高AE,点E为垂足(要求:尺规作图,不写作法,保留作图痕迹);(2)、在射线CD上找一点P,使△PCB与(1)中所作的△ACE全等(要求:尺规作图,不写作法,保留作图痕迹).并证明你所作出的△PCB与△ACE全等.25. 如图,点E在等边△ABC的边AB所在直线上,以EC为一边作等边△ECF,顶点E、C、F顺时针排序. (1)、点E在线段AB上,连接BF.求证:BF//AC;(2)、已知AB=6,当△BCF是直角三角形时,求BE的长.26. 如图1,∠MCN=90°,点A在射线CM上滑动,点B在射线CN上滑动,且线段AB的长始终保持10cm不变.
(1)、点E在线段AB上,连接BF.求证:BF//AC;(2)、已知AB=6,当△BCF是直角三角形时,求BE的长.26. 如图1,∠MCN=90°,点A在射线CM上滑动,点B在射线CN上滑动,且线段AB的长始终保持10cm不变. (1)、若AC=6cm,动点P从点A出发,从点A→点B→点C→点A,速度为2cm/s,设运动时间为ts.当t为何值时,△ACP为等腰三角形;(2)、如图2,在滑动过程中,以AB为斜边在AB的右侧作Rt△ABE,在滑动的过程中EC的最大值为.(直接写出结果)
(1)、若AC=6cm,动点P从点A出发,从点A→点B→点C→点A,速度为2cm/s,设运动时间为ts.当t为何值时,△ACP为等腰三角形;(2)、如图2,在滑动过程中,以AB为斜边在AB的右侧作Rt△ABE,在滑动的过程中EC的最大值为.(直接写出结果)