江苏省扬州市江都区八校2020-2021学年八年级上学期数学期中联考试卷

试卷更新日期：2021-09-18 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2.
如图，字母B所代表的正方形的面积是（　　）

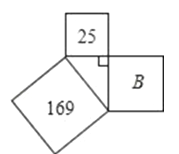A、12 B、144 C、13 D、194

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt[3]{{(- 2)}^{3}} = 2$ B、 $\sqrt{{(- 6)}^{2}} = - 6$ C、 $- \sqrt{25} = - 5$ D、 $\sqrt{9} = \pm 3$

查看试题解析
4. 要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，OA=OB=OC=OD，且点A、O、D与点B、O、C分别共线，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
5. 如图，△ABC的三边AB，BC，CA的长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S_△_ABO∶S_△_BCO∶S_△_CAO等于（）

A、1∶1∶1 B、2∶3∶4 C、2∶1∶3 D、3∶4∶5

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ C = 90^{°}$ ， $A C = 2$ ，点 $D$ 在 $B C$ 上， $∠ A D C = 2 ∠ B$ ， $A D = \sqrt{5}$ ，则 $B C$ 的长为（）

A、 $\sqrt{3} - 1$ B、 $\sqrt{3} + 1$ C、 $\sqrt{5} - 1$ D、 $\sqrt{5} + 1$

查看试题解析
7. 如图所示，数轴上的点A所表示的数为a，则a的值是（）

A、 $\sqrt{5} + 1$ B、 $- \sqrt{5} + 1$ C、 $\sqrt{5} - 1$ D、 $\sqrt{5}$

查看试题解析
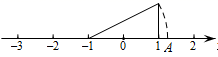8. 如图，在 $Rt △ ABC$ 中， $∠ BAC = 90 °$ ， $∠ B = 36 °$ ，AD是斜边BC上的中线，将△ACD沿AD对折，使点C落在点F处，线段DF与AB相交于点E，则∠BED等于（）

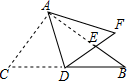A、120° B、108° C、72° D、36°

查看试题解析

二、填空题

9. $\sqrt{16}$ 的平方根是．

查看试题解析
10. 若x、y为实数，且 ${(a + \sqrt{3})}^{2} + \sqrt{b - 2}$ ＝0，则a^b的值＝

查看试题解析
11. 如图，AB=AC，DB=DC，若∠ABC为60°，BE=3cm，则AB=cm.

查看试题解析
12. 如图，在 $△ ABC$ 中， $AB = AC$ ，AB的垂直平分线DE交AC于 $E .$ 若 $∠ A = 40^{\circ}$ ，则 $∠ EBC$ 的度数是.

查看试题解析
13. 等腰三角形 $A B C$ 的周长为 $16 c m$ ，其中 $A B$ 为 $4 c m$ ，则 $B C$ 为.

查看试题解析
14. 已知一个正数的两个平方根分别是2m+1和3﹣m，那么这个正数是.

查看试题解析
15. 如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=6，则CP的长为.

查看试题解析
16. 如图是一个底面为等边三角形的三棱镜，在三棱镜的侧面上，从顶点A到顶点A′镶有一圈金属丝，已知此三棱镜的高为8cm，底面边长为2cm，则这圈金属丝的长度至少为cm.

查看试题解析
17. 如图，“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形，是我国古代数学的骄傲，巧妙地利用面积关系证明了勾股定理、已知小正方形的面积1，直角三角形的两直角边分别为 $a$ 、 $b$ 且 $a b = 6$ ，则图中大正方形的边长为.

查看试题解析
18. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 °$ ， $AC = 6$ ， $BC = 8$ ，AD是 $∠ BAC$ 的平分线.若P，Q分别是AD和AC上的动点，则 $PC + PQ$ 的最小值是.

查看试题解析

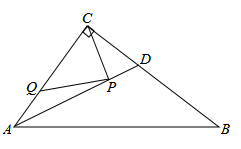
三、解答题

19. 解方程

(1)、 $3 （ x - 2 ）^{2} - \frac{1}{12} = 0$

(2)、 $（ 2 x - 1 ）^{3} - 8 = 0$ .

查看试题解析
20. 作图题：如图是每一个小方格都是边长为1的正方形网格，

(1)、利用网格线作图：找一格点 $P$ ，使点 $P$ 到 $A B$ 和 $A C$ 的距离相等，并且 $P B = P C$ .

(2)、求四边形 $A B P C$ 的面积.

查看试题解析
21. 实数 $a ， b ， c$ 表示在数轴上如图所示，完成下列问题，

试化简： $\sqrt{{(a - c)}^{2}} - | b - a | + \sqrt[3]{{(b - c)}^{3}}$

查看试题解析
22. 如图，点 $O$ 为等边三角形 $A B C$ 内一点，连接 $O A$ ， $O B$ ， $O C$ ，以 $O B$ 为一边作 $∠ O B M = 60^{O}$ ，且 $B O = B M$ ，连接 $C M$ 、 $O M$ .

(1)、判断 $A O$ 与 $C M$ 的大小关系并证明；

(2)、若 $O A = 8$ ， $O C = 6$ ， $O B = 10$ ，判断 $Δ O M C$ 的形状并证明.

查看试题解析
23. 如图，一高层住宅发生火灾，消防车立即赶到距大厦8米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长17米，云梯底部距地面2米，问：发生火灾的住户窗口距离地面多少米？

查看试题解析
24. 如图，在△ABC中，AD是△ABC的高线，CE是△ABC的角平分线，它们相交于点P．

(1)、若∠B＝40°，∠AEC＝75°，求证：AB＝BC；

(2)、若∠BAC＝90°，AP为△AEC边EC上中线，求∠B的度数．

查看试题解析
25. 细心观察图，认真分析下列各式，然后解答问题.

${(\sqrt{1})}^{2} + 1 = 2$ ， $S_{1} = \frac{\sqrt{1}}{2}$ ； ${(\sqrt{2})}^{2} + 1 = 3$ ， $S_{2} = \frac{\sqrt{2}}{2}$ ； ${(\sqrt{3})}^{2} + 1 = 4$ ， $S_{3} = \frac{\sqrt{3}}{2}$ ；....

(1)、请用含有n（n是正整数）的等式表示上述变化规律.

(2)、推算出 $O A_{10}$ 的长.

(3)、求 $S_{1}^{2} + S_{2}^{2} + \dots + S_{10}^{2}$ 的值.

查看试题解析
26. 如图1，四边形 $O A B C$ 中， $O A = a$ ， $O C = 8$ ， $∠ A O C = ∠ B C O = 90 °$ ，经过点 $O$ 的直线 $l$ 将四边形分成两部分，直线 $l$ 与 $O C$ 所成的角设为 $θ$ ，将四边形 $O A B C$ 的直角 $∠ O C B$ 沿直线 $l$ 折叠，点 $C$ 落在点 $D$ 处（如图1）.

(1)、若点 $D$ 与点 $A$ 重合，则 $θ =$ ， $a =$ ；

(2)、若折叠后点 $D$ 恰为 $A B$ 的中点（如图2），则 $θ$ 的度数为.

(3)、在（2）的条件下，求证： $O E = B E + O A$ .

查看试题解析
27. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 3$ ，若动点 $P$ 从点 $C$ 开始，按 $C \to A \to B$ 的路径运动，速度为每秒1个单位长度，设出发的时间为 $t$ 秒.

(1)、出发2秒后，求 $△ A B P$ 的周长.

(2)、问 $t$ 为何值时， $△ B C P$ 为等腰三角形？

查看试题解析
28. 定义：如果三角形有一边上的中线长恰好等于这边的长，那么这个三角形叫“恰等三角形”，这条中线叫“恰等中线”.
（直角三角形中的“恰等中线”）

(1)、如图1，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = \sqrt{3}$ ， $B C = 2$ ， $A M$ 为 $△ A B C$ 的中线.
求证： $A M$ 是“恰等中线”.（等腰三角形中的“恰等中线”）

(2)、已知，等腰 $△ A B C$ 是“恰等三角形”， $A B = A C = 20$ ，求底边 $B C$ 的平方.

查看试题解析