江苏省苏州工业园区2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-18 类型：期中考试

进入出卷网下载

一、单选题

1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $- 0.101101110111 ， \sqrt{7} ， \frac{22}{7} ， - \frac{π}{2} ， \sqrt[3]{8} ， 0$ 中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在平面直角坐标系中，将点P（﹣2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P′的坐标是（）

A、（2，4） B、（1，5） C、（1，-3） D、（-5，5）

查看试题解析
4. 下列各式中，正确的是（）

A、 $\pm \sqrt{16} = \pm 4$ B、 ${(- \sqrt{2})}^{2} = 4$ C、 $\sqrt[3]{- 9} = - 3$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
5. 下列关系：①面积一定的长方形的长s与宽a；②圆的周长s与半径a；③正方形的面积s与边长a；④速度一定时行驶的路程s与行驶时间a，其中s是a的正比例函数的有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，Rt△ABC中，∠ACB＝90°，∠A＝55°，将其折叠，使点A落在边CB上 $A^{'}$ 处，折痕为CD，则 $∠ A^{'} D B$ ＝（）

A、40° B、30° C、20° D、10°

查看试题解析
7. 给出下列说法：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；

②三角形的三边a、b、c满足a²+c²＝b² ，则∠C＝90°；

③△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；

④△ABC中，若a：b：c＝1：2： $\sqrt{3}$ ，则这个三角形是直角三角形.

其中，错误的说法的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（）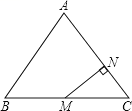

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{6}{5}$ D、 $\frac{16}{5}$

查看试题解析
9. 如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃.若S₁+S₂+S₃=₁₅ ，则S₂的值是（）

A、5 B、 $\frac{15}{2}$ C、 $\frac{15}{4}$ D、3

查看试题解析
10. 如图，在△ABC中，D是BC边上的中点，连结AD，把△ACD沿AD翻折，得到△AD $C^{'}$ ，D $C^{'}$ 与AB交于点E，连结B $C^{'}$ ，若BD＝B $C^{'}$ ＝2，AD＝3，则点D到A $C^{'}$ 的距离（）

A、 $\frac{2}{\sqrt{3}}$ B、 $\frac{3 \sqrt{3}}{\sqrt{7}}$ C、 $\sqrt{7}$ D、 $\sqrt{13}$

查看试题解析

二、填空题

11. 函数y= $\sqrt{2 x - 3}$ 中自变量x的取值范围是．

查看试题解析
12. 直角三角形的两边长分别为6和8，则该直角三角形斜边上的中线为.

查看试题解析
13. 已知点 $M (1 - 2 m ， m - 1)$ 关于 $x$ 轴的对称点在第二象限，则 $m$ 的取值范围是．

查看试题解析
14. 如图，△ABC为等边三角形，BD⊥AB，BD=AB，则∠DCB= °.

查看试题解析
15. 如图，△ABC中，边AB的中垂线分别交BC、AB于点D、E，AE＝3cm，△ABC的周长为18cm，则△ADC的周长是cm.

查看试题解析
16. 正数a的两个平方根是方程 $3 x + 2 y = 2$ 的一组解，则a＝.

查看试题解析
17. 如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点 $B'$ 处，当 $△ CEB'$ 为直角三角形时，BE的长为

查看试题解析
18. 如图，矩形纸片ABCD中，AB＝5cm，BC＝10cm，CD上有一点E，EC=2cm，AD上有一点P，PA＝6cm，过点P作PF⊥AD交BC于点F，将纸片折叠，使P与E重合，折痕交PF于Q则线段PQ的长是cm.

查看试题解析

三、解答题

19. 求下列各式中x的值.

(1)、 $4 x^{2} - 81 = 0$

(2)、 $64 {(x + 1)}^{3} = 27$

查看试题解析
20. 已知2b+1的立方根是3，3a+2b-1的算术平方根为4，求2b+3a的平方根.

查看试题解析
21. 为了加强公民的节水意识，合理利用水资源，某城市规定用水收费标准如下：每户每月用水量不超过6米³时，水费按0.6元/米³收费；每户每月用水量超过6米³时，超过部分按1元米³收费.设每户每月用水量为x米³ ，应付水费y元.

(1)、每月用水量不超过6米³和超过6米³时，y与x之间的函数关系式，并判断它们是否为一次函数.

(2)、已知某户5月份的用水量为8米³ ，求该用户5月份的水费.

查看试题解析
22. △ABC在方格纸中的位置如图所示，方格纸中的每个小正方形的边长为1个单位，

(1)、△A₁B₁C₁与△ABC关于y轴对称，请你在图中画出△A₁B₁C₁；

(2)、将△ABC向下平移8个单位后得到△A₂B₂C₂ ，请你在图中画出△A₂B₂C₂；请分别写出A₂、B₂、C₂的坐标.

(3)、求△ABC的面积.

查看试题解析
23. 已知：如图∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F.

(1)、试说明：BE=CF；

(2)、若AF=3，BC=4，求△ABC的周长.

查看试题解析
24. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词，翻译为：如图秋千细索OA悬挂于O点，静止时竖直下垂，A点为踏板位置，踏板离地高度为一尺（AC＝1尺）.将它往前推进两步（EB⊥OC于点E，且EB＝10尺），踏板升高到点B位置，此时踏板离地五尺（BD=CE=5尺），求秋千绳索（OA或OB）的长度.

查看试题解析
25. 如图，在四边形ABCD中，∠DAB＝30°，点E为AB的中点，DE⊥AB交AB于点E，DE＝ $\sqrt{3}$ ，BC＝2，CD＝4.

(1)、求∠ABC的度数.

(2)、求CE的长.

查看试题解析
26. 阅读下面的文字，解答问题：
大家知道是 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2} - 1$ ，来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗?

事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分.又例如： $∵ \sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3 ， ∴ \sqrt{7}$ 的整数部分2，小数部分为 $(\sqrt{7} - 2)$ .

(1)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求 $a + b + \sqrt{5}$ 的值；

(2)、已知： $10 + \sqrt{3} = x + y$ 其中x是整数，且0 $<$ y $<$ 1，求x－y的相反数.

查看试题解析
27. 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD＝2：3：4；

(1)、试说明△ABC是等腰三角形；

(2)、已知S_△ABC＝40cm² ，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止.设点M运动的时间为t（秒）.
①若△DMN的边与BC平行，求t的值；

②若点E是边AC的中点，在点M运动的过程中，△MDE能否成为等腰三角形?若能，求出t的值；若不能，请说明理由.

查看试题解析