江苏省南京市联合体2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-09-18 类型:期中考试
一、单选题
-
1. 下列四个图形中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数作为三角形的三边长,其中能构成直角三角形的是( )A、2,3,4 B、3,4,5 C、4,5,6 D、5,6,73. 已知等腰三角形的两边长分别为3和5,则它的周长是( )A、8 B、11 C、13 D、11或134. 如图, ,下列条件中,不能判定 的是( )
2. 下列各组数作为三角形的三边长,其中能构成直角三角形的是( )A、2,3,4 B、3,4,5 C、4,5,6 D、5,6,73. 已知等腰三角形的两边长分别为3和5,则它的周长是( )A、8 B、11 C、13 D、11或134. 如图, ,下列条件中,不能判定 的是( ) A、 B、 C、 D、5. 如图,在 中, ,若 ,则正方形 和正方形 的面积和为( )
A、 B、 C、 D、5. 如图,在 中, ,若 ,则正方形 和正方形 的面积和为( ) A、225 B、200 C、250 D、1506. 如图,在 中, , 为 边上的高, 为 边上的中线, , ,则 的长度是( )
A、225 B、200 C、250 D、1506. 如图,在 中, , 为 边上的高, 为 边上的中线, , ,则 的长度是( ) A、 B、 C、 D、7. 如图, 是 的角平分线, ,垂足为E, , , ,则 长为( )
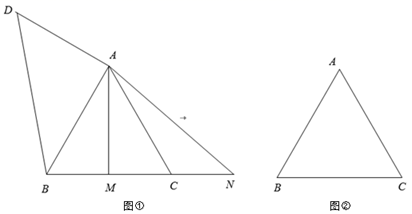
A、 B、 C、 D、7. 如图, 是 的角平分线, ,垂足为E, , , ,则 长为( ) A、 B、 C、 D、8. 已知 中, , , 是 边的中点,点 、 分别在 、 边上运动,且保持 .连接 、 、 得到下列结论:① 是等腰直角三角形;② 面积的最大值是 ;③ 的最小值是 .其中正确的结论是( )
A、 B、 C、 D、8. 已知 中, , , 是 边的中点,点 、 分别在 、 边上运动,且保持 .连接 、 、 得到下列结论:① 是等腰直角三角形;② 面积的最大值是 ;③ 的最小值是 .其中正确的结论是( ) A、②③ B、①② C、①③ D、①②③
A、②③ B、①② C、①③ D、①②③二、填空题
-
9. 角的内部到角两边距离相等的点在上.10. 已知 , , ,则 .11. 已知:如图, ,只需补充条件 , 就可以根据“ ”得到 .
 12. 若等腰三角形的一个内角为 ,则其底角为 .13. 在 中, , , ,则 的面积为.14. 一个直角三角形的两边长分别是 和 ,则第三边长的平方为.15. 如图,在 中, 的垂直平分线 交 于点 , , ,则 的周长为.
12. 若等腰三角形的一个内角为 ,则其底角为 .13. 在 中, , , ,则 的面积为.14. 一个直角三角形的两边长分别是 和 ,则第三边长的平方为.15. 如图,在 中, 的垂直平分线 交 于点 , , ,则 的周长为. 16. 如图,在 中, 平分 , .若 , ,则 的度数为 .
16. 如图,在 中, 平分 , .若 , ,则 的度数为 . 17. 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm,BC=5cm,则重叠部分△DEF的面积为cm 2.
17. 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm,BC=5cm,则重叠部分△DEF的面积为cm 2. 18. 如图,在四边形 中, , , ,若 , ,则点 到 的距离是.
18. 如图,在四边形 中, , , ,若 , ,则点 到 的距离是.
三、解答题
-
19. 如图,点 、 在线段 上, , , .
求证: .
 20. 如图,在 中, ,垂足为点 , , , .
20. 如图,在 中, ,垂足为点 , , , . (1)、求 的长;(2)、求 的长.21. 证明:有两个角相等的三角形是等腰三角形.
(1)、求 的长;(2)、求 的长.21. 证明:有两个角相等的三角形是等腰三角形.
已知:如图,在 中, ▲ ,
求证: ▲ .
证明:
22. 如图,点 、 、 在一条直线上, , , ;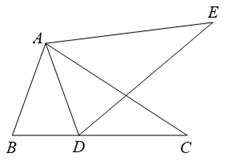 (1)、求证: ;(2)、若 ,求 .23. 如图,在△ABC中,D,E是BC边上两点,AD=AE,∠BAD=∠CAE.求证:AB=AC.
(1)、求证: ;(2)、若 ,求 .23. 如图,在△ABC中,D,E是BC边上两点,AD=AE,∠BAD=∠CAE.求证:AB=AC.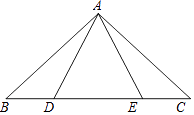 24. 如图,在 中,点 、 在边 上, , ,垂足为 , ,垂足为 , 与 交于点 ,且 .
24. 如图,在 中,点 、 在边 上, , ,垂足为 , ,垂足为 , 与 交于点 ,且 . (1)、求证: ;(2)、连接 ,并延长 交 于点 ,求证:过点 、 的直线垂直平分线段 .
(1)、求证: ;(2)、连接 ,并延长 交 于点 ,求证:过点 、 的直线垂直平分线段 .