江苏省淮安市淮安区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-09-18 类型：期中考试
一、单选题
-
1. 2019年4月28日，北京世界园艺博览会正式开幕.下面分别是北京、西安、锦州、沈阳四个城市举办世园会的标志，其中是轴对称图形的有（ ）
A、 1个 B、2个 C、3个 D、4个2. 如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是（ ）
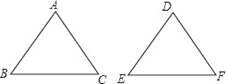A、∠B=∠E，BC=EF B、∠A=∠D，BC=EF C、∠A=∠D，∠B=∠E D、BC=EF，AC=DF3. 如图：若 ，且 ，则EC的长为（ ）
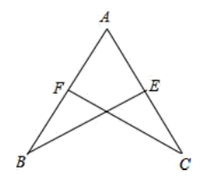A、2 B、2.5 C、3 D、54. 等腰三角形的顶角为 80°，则它的底角为（ ）A、100° B、80° C、50° D、50°或 80°5. 一块三角形草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到三条边的距离都相等，凉亭的位置应造在（ ）A、 的三条角平分线的交点 B、 的三条高所在直线的交点 C、 的三条中线的交点 D、 的三边中垂线的交点6. 下列各组数不能构成直角三角形的是（ ）A、3，4，5 B、6，8，10 C、32 ， 42 ， 52 D、5，12，137. 已知：如图，在△ABC中，边AB的垂直平分线分别交BC、AB于点G、D，若△AGC的周长为31cm，AB=20cm，则△ABC的周长为（ ）
A、31cm B、41cm C、51cm D、61cm8. 如图，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点（点D与A，B不重合），连结CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连结DE交BC于点F，连接BE.当AD＝BF时，∠BEF的度数是（ ）
A、45° B、60° C、62.5° D、67.5°二、填空题
-
9. 等边三角形的对称轴共有条.10. 若一个直角三角形的两直角边长分别为12、5，则其斜边长为.11. 已知等腰三角形的周长为12，底边长为5，则腰长为.12. 小明从镜子中看到对面电子钟如图所示，这时的时刻应是.
13. 如图，△ABC中，∠ACB＝90°，分别以AC、AB为边向外作正方形，面积分别为S1 ， S2 ， 若S1＝2，S2＝5，则BC 2＝.
14. 如图所示，在高为3m，斜坡长为5m的楼梯表面铺地毯，至少需要地毯米.
15. 已知，在 中， ，且 边上的高为12，边BC的长为 ．16. 如图，A.B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有个.
三、解答题
-
17. 如图，已知△ABC中，∠C=90°，DE⊥AB于E，AC=AE.求证：CD=DE.
18. 如图，将 绕直角顶点 按逆时针方向旋转 得到 .已知 ，求 的度数.
19. 如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（请用直尺保留作图痕迹）.
(1)、画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；(2)、△ABC的面积是；(3)、在DE上画出点Q，使△QAB的周长最小.20. 如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O.求证：AB＝CD；
21. 如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E.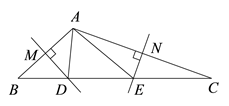
(1)、若BC=5，求△ADE的周长.(2)、若∠BAD+∠CAE=60°，求∠BAC的度数.22. 如图，已知某开发区有一块四边形空地ABCD，现计划在该空地上种植草皮，经测量∠ADC=90°，CD=6m，AD=8m，BC=24m，AB=26m，若每平方米草皮需200元，则在该空地上种植草皮共需多少钱？
23. 如图，△ABC为等边三角形，点M、N分别在BC、AC上，且BM=CN，AM与BN交于Q点.
(1)、求证：△BCN≌△ABM；(2)、求∠AQN的度数.24. 台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力.如图，有一台风中心沿东西方向AB由点A行驶向点B，已知点 C为一海港，且点 C与直线AB上两点A，B的距离分别为300km和400km，又AB=500km，以台风中心为圆心周围250km以内为受影响区域.
(1)、海港C受台风影响吗？为什么？(2)、若台风的速度为20km/h，台风影响该海港持续的时间有多少小时？25. 把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF.若AB = 3 cm，BC = 5 cm，
(1)、重叠部分△DEF的面积是多少?(2)、求FC的长.26. 如图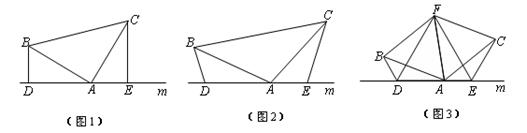
(1)、如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E.证明：DE=BD+CE.(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC= ，其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立，请你给出证明；若不成立，请说明理由.(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.