江苏省海安县西片11校22020-2021学年八年级上学期数学期中联考试卷

试卷更新日期：2021-09-18 类型：期中考试

进入出卷网下载

一、单选题

1. 如果一个三角形的两边长分别是2和5，则第三边可能是（）

A、2 B、3 C、5 D、8

查看试题解析
2. 若 $a \neq 0$ ，化简下列各式，正确的个数有（）
① $a^{0} \cdot a \cdot a^{5} = a^{5}$ ；② ${(a^{2})}^{3} = a^{6}$ ；③ ${(- 2 a^{4})}^{3} = - 6 a^{12}$ ；④ $a \div a^{- 2} = a^{3}$

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（）

A、SAS B、ASA C、SSS D、AAS

查看试题解析
4. 下列运算中正确的是（）
① $(x + 2) (x - 2) = x^{2} - 2$ ；② $(- 3 a - 2) (3 a - 2) = 4 - 9 a^{2}$ ；③ ${(a + b)}^{2} = a^{2} + b^{2}$ ；④ ${(a - b)}^{2} = a^{2} - a b + b^{2}$

A、1 B、2 C、3 D、4

查看试题解析
5. 如图所示，Rt△ABC中，∠C＝90°，AB的垂直平分线DE交BC于D，交AB于点E.当∠B＝30°时，图中一定不相等的线段有（）.

A、AC＝AE＝BE B、AD＝BD C、CD＝DE D、AC＝BD

查看试题解析
6. 下列各式能用公式法因式分解的是（）

A、 $- x^{2} + y^{2}$ B、 $- x^{2} - y^{2}$ C、 $4 x^{2} + 4 x y - y^{2}$ D、 $x^{2} + x y + y^{2}$

查看试题解析
7. 如图，在△ABC中，∠ACB＝70°，∠1＝∠2.则∠BPC的度数为（）

A、70 B、108 C、110 D、125

查看试题解析
8. 若x²+y²+4x﹣6y+13=0，则式子x﹣y的值等于（）

A、﹣1 B、1 C、﹣5 D、5

查看试题解析
9. 如图，已知 $C D ⊥ A B$ 于D，现有四个条件：（1） $A D = E D$ ；（2） $∠ A = ∠ B E D$ ；（3） $∠ C = ∠ B$ ；（4） $A C = E B$ .那么不能得出 $△ A D C ≌ △ E D B$ 的条件是（）

A、（1）（3） B、（2）（4） C、（1）（4） D、（2）（3）

查看试题解析
10. 下列比较大小：① $2^{100}$ _______ $3^{75}$ ；② $\sqrt{15} - \sqrt{14}$ _______ $\sqrt{14} - \sqrt{13}$ 正确的是（）

A、①＜；②＜ B、①＜；②＞ C、①＞；②＜ D、①＞；②＞

查看试题解析

二、填空题

11. 要使式子 $\frac{1}{x (x - 1)}$ 有意义，则x的取值范围为.

查看试题解析
12. 点 $A (\begin{matrix} a ， 5 \end{matrix})$ ， $B (\begin{matrix} 3 ， b \end{matrix})$ 关于x轴对称，则 $a + b =$ .

查看试题解析
13. 若 $x - y = 6$ ， $x y = 7$ ，则 $x^{2} + y^{2}$ 的值等于.

查看试题解析
14. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ， $B E ⊥ A C$ ， $C F ⊥ A B$ ，垂足分别是D，E，F.若 $A C = 4$ ， $A D = 3$ ， $B E = 2$ ，则 $B C =$ .

查看试题解析
15. 若 $x^{2} + k x + 16$ 是一个完全平方式，则k= ．

查看试题解析
16. 如图，在 $△ A B C$ 中，E为AC的中点，AD平分∠BAC，BA：CA＝2：3，AD与BE相交于点O，若 $△ O A E$ 的面积比 $△ B O D$ 的面积大1，则 $△ A B C$ 的面积是.

查看试题解析
17. 已知 $x = a$ 时，多项式 $x^{2} + 4 x + 4 b^{2}$ 的值为 $- 4$ ，则 $x = - a$ 时，该多项式的值为.

查看试题解析
18. 如图，平面直角坐标系xOy中，已知定点 $A (1 ， 0)$ 和 $B (0 ， 1)$ ，若动点C在x轴上运动，则使 $△ A B C$ 为等腰三角形的点C有个.

查看试题解析

三、解答题

19. 计算和因式分解.

(1)、计算： ${0.125}^{9} \times {(- 8)}^{10} + {(\frac{2}{5})}^{11} \times {(2 \frac{1}{2})}^{12}$ ；

(2)、计算： ${(2 x + 1)}^{2} - 2 (x + 1) (x - 1)$ .

(3)、因式分解： $- 3 x^{2} + 6 x y - 3 y^{2}$ ；

(4)、因式分解： $a^{2} (x - y) + 16 (y - x)$ .

查看试题解析
20.

(1)、若 $(x^{2} + m x - 8) (x^{2} - 3 x + n)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，求 $2 m + n$ 的值.

(2)、已知 $a - 2 b = \frac{1}{2}$ ， $a b = 2$ ，求： $- a^{4} b^{2} + 4 a^{3} b^{3} - 4 a^{2} b^{4}$ 的值.

查看试题解析
21. 如图，四边形ABCD中，∠B=90°， AB//CD，M为BC边上的一点，AM平分∠BAD，DM平分∠ADC，

求证：

(1)、AM⊥DM；

(2)、M为BC的中点.

查看试题解析
22. 如图，在平面直角坐标系中，点 $A (1 ， 3)$ ，点 $B (3 ， 1)$ ，点 $C (4 ， 5)$ .

(1)、画出 $△ A B C$ 关于y轴的对称图形 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、若点P在x轴上，连接PA、PB，是否存在一点P，使 $P A + P B$ 的值最小，若存在，请在图中标出点P的位置；

(3)、若直线 $M N // y$ 轴，与线段AB、AC分别交于点M、N（点M不与点A重合），若将 $△ A M N$ 沿直线MN翻折，点A的对称点为点 $A^{'}$ ，当点 $A^{'}$ 落在 $△ A B C$ 的内部（包含边界）时，点M的横坐标m的取值范围是.

查看试题解析
23. 下面是某同学对多项式（x²－4x+2）（x²－4x+6）+4进行因式分解的过程.
解：设x²－4x=y

原式=（y+2）（y+6）+4 （第一步）

= y²+8y+16 （第二步）

=（y+4）² （第三步）

=（x²－4x+4）²（第四步）

回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的_______.

A、提取公因式 B、平方差公式 C、完全平方公式

(2)、该同学因式分解的结果是否彻底？.（填“彻底”或“不彻底”），若不彻底，请直接写出因式分解的最后结果.

(3)、请你模仿以上方法尝试对多项式（x²－2x）（x²－2x+2）+1进行因式分解.

查看试题解析
24. 如图，在等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q三点在一条直线上，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试证明你的结论．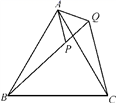

查看试题解析
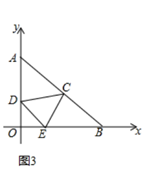
25. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂.

(1)、用含a，b的代数式分别表示S₁、S₂；

(2)、若a+b＝10，ab＝20，求S₁+S₂的值；

(3)、当S₁+S₂＝30时，求出图3中阴影部分的面积S₃.

查看试题解析
26. 如图1，像 $∠ G = ∠ H M N = ∠ Q = ∠ α$ 这样，由 $△ G H M$ 和 $△ M N Q$ 组合成的封闭图形，我们称之为K型GHMNQ.在平面直角坐标系中， $A (0 ， 6)$ ， $B (6 ， 0)$ ，点C，D，E分别在线段AB，AO，BO上运动，且ADCEB为K型.

(1)、如图2，若点D运动到点O时，过点O作 $O F ⊥ C O$ ，交CE的延长线为F，连接BF，求证： $△ A C O ≌ △ B F O$ ；

(2)、如图3，若C是AB的中点，当 $△ D C E$ 为等腰三角形时，请直接写出AD的长.

查看试题解析