江苏省常州市金坛区2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-09-18 类型：期中考试

进入出卷网下载

一、单选题

1. 2020年5月1日起，北京市全面推行生活垃圾分类.下面图标分别为厨余垃圾、可回收物、有害垃圾、其他垃圾，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
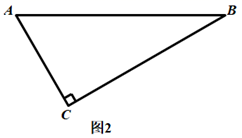
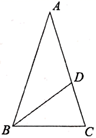
2. 如图，∠B=∠C，点D在AB上，点E在AC上.补充下列一个条件后，仍不能判定△ABE与△ACD全等的是（）

A、AB=AC B、BE=CD C、AD=AE D、∠AEB=∠ADC

查看试题解析
3. 如图，在 $R t Δ A B C$ 中， $∠ B = 90^{°} ， E D$ 是 $A C$ 的垂直平分线，交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E$ .已知 $∠ B A E = 10^{°}$ ，则 $∠ C$ 的度数为（）

A、 $30^{°}$ B、 $40^{°}$ C、 $50^{°}$ D、 $60^{°}$

查看试题解析
4. 如图，在四边形ABCD中， $A D // B C$ ，DE平分 $∠ A D C$ 交BC于点E，若 $B C = 10 cm$ ， $B E = 4 cm$ ，则CD的长是（）

A、2cm B、4cm C、6cm D、8cm

查看试题解析
5. 下列各组线段中，能作为直角三角形三边的是（）

A、3，4，6 B、5，12，15 C、9，12，16 D、6，8，10

查看试题解析
6. 如图，四边形AFDC是正方形， $∠ C E A$ 和 $∠ A B F$ 都是直角，且E，A，B三点共线， $A B = 4$ ，则图中阴影部分的面积是（）

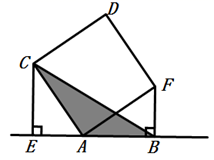A、12 B、10 C、8 D、6

查看试题解析
7. 如图，已知 $△ A B C$ 中， $A B = A C = 4$ ， $B C = 6$ ，在BC边上取一点P（点P不与点B、C重合），使得 $△ A B P$ 成为等腰三角形，则这样的点P共有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）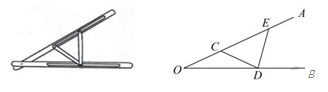

A、60° B、65° C、75° D、80°

查看试题解析

二、填空题

9. 等腰三角形的一个内角120°，则它的底角是.

查看试题解析
10. 已知一个等腰三角形的两边长分别为3和6，则等腰三角形的周长是.

查看试题解析
11. 三角形三边长分别为3，4，5，那么最长边上的中线长等于．

查看试题解析
12. 等腰三角形腰长为10cm，底边上的高为8cm，则等腰三角形的面积是 ${cm}^{2}$ .

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $c = 1$ ，则 $a^{2} + b^{2} + c^{2} =$ .

查看试题解析
14. 如图，点 $D$ 在 $△ ABC$ 的边 $BC$ 上，且 $BC = BD + AD$ ，则点 $D$ 在的垂直平分线上.

查看试题解析
15. 如图，已知在等边三角形ABC中，点E在AC上，点F在BC上，且 $A E = C F$ ，AF、BE相交于点O，则 $∠ B O F =$ °.

查看试题解析
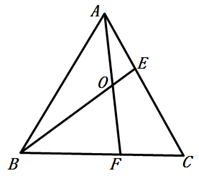16. 如图，已知 $∠ A B C = ∠ A D C = 90 °$ ，M、N分别是AC、BD的中点若 $M N = 3$ ， $B D = 8$ ，则 $A C =$ .

查看试题解析
17. 如图是由8个全等的长方形组成的大正方形，线段AB的端点都在小长方形的顶点上，如果点P是某个小长方形的顶点，连接AP，BP，那么使 $△ A B P$ 为等腰直角三角形的点P有个.

查看试题解析
18. 如图， $Rt △ A B C$ 纸片的直角边AC落在直线l上， $∠ A C B = 90 °$ ， $A C = 5$ ， $B C = 6$ ，平面内一点O到直线l的距离为9， $Rt △ A B C$ 纸片沿直线l左右移动，则 $O A + O B$ 的最小值是.

查看试题解析

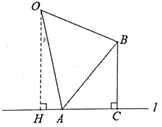
三、解答题

19. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 36 °$ ，BD平分 $∠ A B C$ 交AC于点D.

(1)、求 $∠ A B D$ 的度数.

(2)、求证： $A D = B C$ .

查看试题解析
20. 如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，BD=CE，BE、CD相交于点0；

求证：

(1)、 $Δ D B C ≅ Δ E C B$

(2)、 $O B = O C$

查看试题解析
21. 如图，点A，B，C，D在一条直线上， $E A // F B$ ， $E A = F B$ ， $A B = C D$ .

(1)、求证： $∠ E = ∠ F$ .

(2)、若 $E A = C A$ ， $∠ A = 40 °$ ，求 $∠ D$ 的度数.

查看试题解析
22. 如图，已知 $Rt △ A B C$ 和 $Rt △ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ，点C在线段BE上，连接DC交AE于点O.

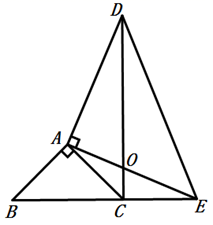(1)、DC与BE有怎样的位置关系？证明你的结论；

(2)、若 $B C = 7$ ， $C E = 5$ ，求DE的长.

查看试题解析
23. 如图，在长方形ABCD中，点E在CD边上，将 $△ B C E$ 沿BE折叠，点C落在AD边上的点F处，过点F作 $F G // C D$ 交BE于点G.

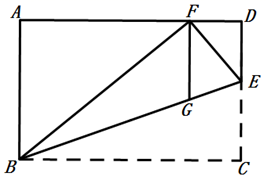(1)、判断 $△ E F G$ 的形状，证明你的结论；

(2)、若 $A B = 6$ ， $A D = 10$ ，求 $△ D E F$ 的面积.

查看试题解析
24. 解答题

(1)、如图2，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ，P是BC边一点.

①用直尺和圆规在AB边上求作一点Q，使得 $∠ A Q C = ∠ P Q B$ .（保留作图痕迹，不要求写作法）.

②在①的条件下，若 $∠ A = 60 °$ ，点Q是AB边的中点，那么点P是BC边的中点吗？证明你的结论.

(2)、如图1，EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF.求证： $∠ A F E = ∠ C F D$ .

查看试题解析
25. 如图，已知 $△ A B C$ 中， $A B = A C = 2$ ， $B C^{2} = 8$ .

(1)、求 $∠ A B C$ 的度数；

(2)、在直线BC上取一点P，在射线AC上取一点Q，若 $△ A B P$ 与 $△ C P Q$ 全等，求 $∠ A P B$ 的度数.

查看试题解析