福建省福州市晋安区九校2020-2021学年八年级上学期数学期中联考试卷
试卷更新日期:2021-09-18 类型:期中考试
一、单选题
-
1. 在以下回收、绿色食品、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个三角形的两边长分别是3cm和8cm,则此三角形的第三边的长可能是( )A、3cm B、5cm C、8cm D、11cm3. 如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )
2. 一个三角形的两边长分别是3cm和8cm,则此三角形的第三边的长可能是( )A、3cm B、5cm C、8cm D、11cm3. 如图,△ABC≌△DEC,∠ACB=90°,∠DCB=20°,则∠BCE的度数为( )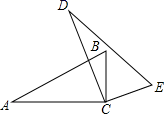 A、20° B、40° C、70° D、90°4. 如图,在△ABC中,AD交边BC于点D.设△ABC的重心为M, 若点M在线段AD上,则下列结论正确的是( )
A、20° B、40° C、70° D、90°4. 如图,在△ABC中,AD交边BC于点D.设△ABC的重心为M, 若点M在线段AD上,则下列结论正确的是( )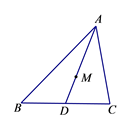 A、∠BAD=∠CAD B、AM=DM C、△ABD的周长等于△ACD的周长 D、△ABD的面积等于△ACD的面积5. 在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )A、(3,2) B、(3,﹣2) C、(﹣3,2) D、(﹣3,﹣2)6. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )
A、∠BAD=∠CAD B、AM=DM C、△ABD的周长等于△ACD的周长 D、△ABD的面积等于△ACD的面积5. 在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )A、(3,2) B、(3,﹣2) C、(﹣3,2) D、(﹣3,﹣2)6. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )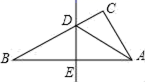 A、10cm B、12cm C、15cm D、17cm7. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A、10cm B、12cm C、15cm D、17cm7. 如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )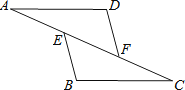 A、∠A=∠C B、∠D=∠B C、AD∥BC D、DF∥BE8. 在△ABC中,D,E分别是边AB,AC上的点,且AD=CE,∠DEC=∠C=70°,∠ ADE=30°,则下列结论正确的是( )A、DE=CE B、BC=CE C、DB=DE D、AE=DB9. 在平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0)(m<6),若△POA是等腰三角形,则m可取的值最多有( )A、2个 B、3个 C、4个 D、5个10. 如图,点 在线段 上,若 ,且 , , ,则下列角中,大小为 的角是
A、∠A=∠C B、∠D=∠B C、AD∥BC D、DF∥BE8. 在△ABC中,D,E分别是边AB,AC上的点,且AD=CE,∠DEC=∠C=70°,∠ ADE=30°,则下列结论正确的是( )A、DE=CE B、BC=CE C、DB=DE D、AE=DB9. 在平面直角坐标系中,O是坐标原点,点A(3,2),点P(m,0)(m<6),若△POA是等腰三角形,则m可取的值最多有( )A、2个 B、3个 C、4个 D、5个10. 如图,点 在线段 上,若 ,且 , , ,则下列角中,大小为 的角是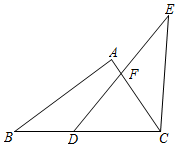 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在△ABC中,已知∠A=60°,∠B=80°,则∠C=.12. 正五边形的内角和等于度.13. 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是
 14. 如图,把长方形纸片ABCD沿对角线折叠,若∠BDE =25°,那么∠BED =.
14. 如图,把长方形纸片ABCD沿对角线折叠,若∠BDE =25°,那么∠BED =.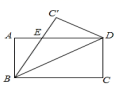 15. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为.
15. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为.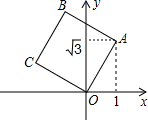 16. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为.
16. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为.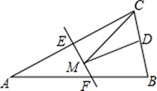
三、解答题
-
17. 一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.18. 如图,AB=AC,AD=AE.求证:∠B=∠C.
 19. 如图,已知锐角∠MPN,点A在射线PN上.
19. 如图,已知锐角∠MPN,点A在射线PN上.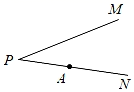 (1)、尺规作图:在射线PM上求作点B,使得BP=BA;(保留作图痕迹,不写作法)(2)、在射线AN上截取AC=PB,试判断∠BCP和∠MPN的数量关系,并说明理由.20. 如图,已知 的三个顶点的坐标分别为 , , .
(1)、尺规作图:在射线PM上求作点B,使得BP=BA;(保留作图痕迹,不写作法)(2)、在射线AN上截取AC=PB,试判断∠BCP和∠MPN的数量关系,并说明理由.20. 如图,已知 的三个顶点的坐标分别为 , , .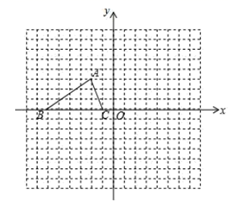 (1)、将 向右平移6个单位,再向下平移3个单位得到 ,图中画出 ,求平移后点A对应点 的坐标.(2)、将 沿y轴翻折得 ,图中画出 ,求翻折后点A对应点 坐标.(3)、若将 向左平移2个单位,求: 扫过的面积.21. 证明:等腰三角形两底角的角平分线相等.22. 如图,在 中,以AB为边作等边△ABD(点C、D在边AB的同侧),连接CD.若∠ABC=90°,∠BAC=30°,求∠BDC的度数.
(1)、将 向右平移6个单位,再向下平移3个单位得到 ,图中画出 ,求平移后点A对应点 的坐标.(2)、将 沿y轴翻折得 ,图中画出 ,求翻折后点A对应点 坐标.(3)、若将 向左平移2个单位,求: 扫过的面积.21. 证明:等腰三角形两底角的角平分线相等.22. 如图,在 中,以AB为边作等边△ABD(点C、D在边AB的同侧),连接CD.若∠ABC=90°,∠BAC=30°,求∠BDC的度数.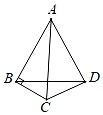 23. 我们常用各种多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些多边形,能够拼成一个平面图形,既不留一丝空白,又不互相重叠,这在几何里叫做平面密铺(镶嵌).我们知道,当围绕一点拼在一起的几个多边形的内角的和为360°时,就能够拼成一个平面图形.某校研究性学习小组研究平面密铺的问题,其中在探究用两种边长相等的正多边形做平面密铺的情形时用了以下方法:如果用x个正三角形、y个正六边形进行平面密铺,可得60°•x+120°•y=360°,化简得x+2y=6.因为x、y都是正整数,所以只有当x=2,y=2或x=4,y=1时上式才成立,即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形,如图(1)、(2)、(3).
23. 我们常用各种多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些多边形,能够拼成一个平面图形,既不留一丝空白,又不互相重叠,这在几何里叫做平面密铺(镶嵌).我们知道,当围绕一点拼在一起的几个多边形的内角的和为360°时,就能够拼成一个平面图形.某校研究性学习小组研究平面密铺的问题,其中在探究用两种边长相等的正多边形做平面密铺的情形时用了以下方法:如果用x个正三角形、y个正六边形进行平面密铺,可得60°•x+120°•y=360°,化简得x+2y=6.因为x、y都是正整数,所以只有当x=2,y=2或x=4,y=1时上式才成立,即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形,如图(1)、(2)、(3).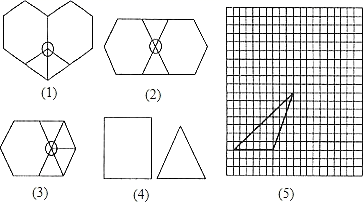 (1)、请你仿照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形,并按图(4)中给出的正方形和正三角形的大小大致画出密铺后图形的示意图(只要画出一种图形即可);(2)、如果用形状、大小相同的如图(5)方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图.24. 在 中,∠BAC=90°,AB=AC,点P为AC上一点,点M为BC上一点,线段AM,BP交于点E.(1)、如图1,若BP为 的角平分线,且AM⊥BC,求证:AE=AP.
(1)、请你仿照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形,并按图(4)中给出的正方形和正三角形的大小大致画出密铺后图形的示意图(只要画出一种图形即可);(2)、如果用形状、大小相同的如图(5)方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图.24. 在 中,∠BAC=90°,AB=AC,点P为AC上一点,点M为BC上一点,线段AM,BP交于点E.(1)、如图1,若BP为 的角平分线,且AM⊥BC,求证:AE=AP.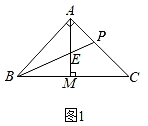 (2)、如图2,若BP为 的角平分线,且AM⊥BP,求证:AP=PM.
(2)、如图2,若BP为 的角平分线,且AM⊥BP,求证:AP=PM.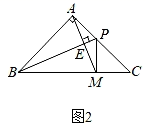 (3)、如图3,若BP为 的中线,且AM⊥BP,求证:BP=AM+MP.
(3)、如图3,若BP为 的中线,且AM⊥BP,求证:BP=AM+MP.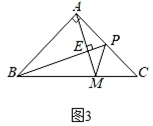 25. 如图,在平面直角坐标系中,点A为x轴负半轴上一点,B为y轴正半轴上一点,若AO=2,AB=2OA.
25. 如图,在平面直角坐标系中,点A为x轴负半轴上一点,B为y轴正半轴上一点,若AO=2,AB=2OA.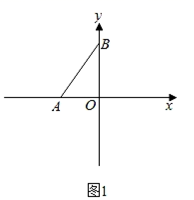 (1)、作A点关于y轴的对称点E,并写出E点的坐标;(2)、求∠BAO的度数;(3)、如图2,P是射线OA上任意一点,以PB为边向上作等边三角形 ,DA的延长线交y轴于点Q,
(1)、作A点关于y轴的对称点E,并写出E点的坐标;(2)、求∠BAO的度数;(3)、如图2,P是射线OA上任意一点,以PB为边向上作等边三角形 ,DA的延长线交y轴于点Q,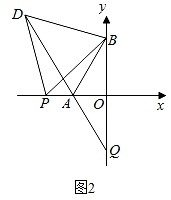
①求AQ的长;
②若OB=2 ,求BD的最小值.