新疆乌鲁木齐市沙依巴克区2021年数学中考三模试卷

试卷更新日期：2021-09-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -22的绝对值等于( )

A、-22 B、- $\frac{1}{22}$ C、 $\frac{1}{22}$ D、22

查看试题解析
2. 如图所示的三视图表示的几何体是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 $x^{6} \div x^{5} = x$ C、 ${(- x^{2})}^{4} = x^{6}$ D、 $x^{2} + x^{3} = x^{5}$

查看试题解析
4. AF是 $∠ B A C$ 的平分线， $D F / / A C ，$ 若 $∠ B A C = 70 ° ，$ 则 $∠ 1$ 的度数为（）

A、17.5° B、35° C、55° D、70°

查看试题解析
5. 方程2x²﹣8x﹣1＝0的解的情况是（）

A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根

查看试题解析
6. 小韦和小黄进行射击比赛，各射击6次，根据成绩绘制的两幅折线统计图如下，以下判断正确的是（）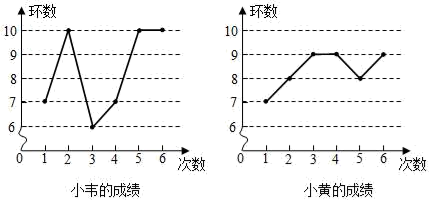

A、小黄的成绩比小韦的成绩更稳定 B、两人成绩的众数相同 C、小韦的成绩比小黄的成绩更稳定 D、两人的平均成绩不相同

查看试题解析
7. 某旅店一共70个房间，大房间每间住8个人，小房间每间住6个人，一共480个学生刚好住满，设大房间有 $x$ 个，小房间有 $y$ 个.下列方程正确的是（）

A、 ${\begin{matrix} x + y = 70 \\ 8 x + 6 y = 480 \end{matrix}$ B、 ${\begin{matrix} x + y = 70 \\ 6 x + 8 y = 480 \end{matrix}$ C、 ${\begin{matrix} x + y = 480 \\ 6 x + 8 y = 70 \end{matrix}$ D、 ${\begin{matrix} x + y = 480 \\ 8 x + 6 y = 70 \end{matrix}$

查看试题解析
8. 若不等式组 ${\begin{array}{l} x + 7 > 3 x - 3 \\ x - 1 < m \end{array}$ 的解集为x＜5，则m的取值范围为（）

A、m＜4 B、m≤4 C、m≥4 D、m＞4

查看试题解析
9. 对称轴为直线x＝1的抛物线 $y = a x^{2} + b x + c$ （a、b、c为常数，且a≠0）如图所示，小明同学得出了以下结论：①abc＜0，②b²＞4ac，③4a＋2b＋c＞0，④3a＋c＞0，⑤a＋b≤m(am＋b)（m为任意实数）， ⑥当x＜－1时，y随x的增大而增大，其中结论正确的个数为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

10. 分解因式： $x^{2} y - y$ =.

查看试题解析
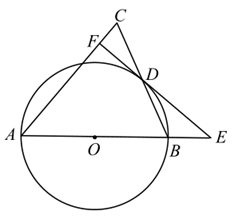
11. 函数 $y = - x$ 与 $y = \frac{k}{x} (k \neq 0)$ 的图象无交点，且 $y = \frac{k}{x}$ 的图象过点 $A (1 ， y_{1})$ ， $B (2 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ .（填>，<或=）

查看试题解析
12. 在平面直角坐标系中，已知两点坐标A(m-1,3), B(1,m²-1)，若AB∥x轴，则m的值是.

查看试题解析
13. 如图，AB是⊙O的直径，AC是弦， $A C = 3$ ， $∠ BOC = 2 ∠ A O C$ .若用扇形 $O A C$ （图中阴影部分）围成一个圆锥的侧面，则这个圆锥底面圆的半径是.

查看试题解析
14. 如图①是长方形纸带， $∠ D E F = α$ ，将纸带沿 $E F$ 折叠成图②，再沿 $B F$ 折叠成图③，则图③中的 $∠ C F E$ 的度数是.

查看试题解析
15. 如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为.

查看试题解析

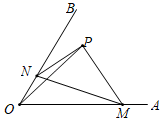
三、解答题

16. 计算： $2 \sin 45 ° + {(3 - π)}^{0} + | \sqrt{2} - \sqrt[3]{8} | - {(\frac{1}{2})}^{- 1}$

查看试题解析
17. 先化简，再求值： $\frac{x + 1}{x^{2} - 4} \cdot (\frac{1}{x + 1} + 1)$ ，其中 $x = 3$ .

查看试题解析
18. 如图，菱形ABCD的对角线AC与BD相交于O，E是BC中点，连接OE并延长到F，使EF＝OE．

(1)、求证：四边形OBFC是矩形．

(2)、如果作BG∥OF，FG∥BC，四边形BGFE是何特殊四边形？并说明理由．

查看试题解析

19. 为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图.

男、女生所选类别人数统计表

类别	男生（人）	女生（人）
文学类	12	8
史学类	$m$	5
科学类	6	5
哲学类	2	$n$

根据以上信息解决下列问题

(1)、

m =

，

n =

；

(2)、扇形统计图中“科学类”所对应扇形圆心角度数为

°

；

(3)、从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率.

查看试题解析

20. 为迎接“五一”国际劳动节，某商场计划购进甲、乙两种品牌的 $T$ 恤衫共100件，已知乙品牌每件的进价比甲品牌每件的进价贵30元，且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.

(1)、求甲、乙两种品牌每件的进价分别是多少元？

(2)、商场决定甲品牌以每件50元出售，乙品牌以每件100元出售.为满足市场需求，购进甲种品牌的数量不少于乙种品牌数量的4倍，请你确定获利最大的进货方案，并求出最大利润.

查看试题解析
21. 如图，某高楼顶部有一信号发射塔，在矩形建筑物 $A B C D$ 的 $A ， C$ 两点测得该塔顶端 $E$ 的仰角分别为 $∠ α = 48^{°}$ 和 $∠ β = 65^{°}$ ，矩形建筑物的宽度 $A D = 18 m$ ，高度 $C D = 30 m$ ，求信号发射塔顶端到地面的距离 $E F$ . （结果精确到 $0.1 m$ ）
（参考数据： $s i n 48^{°} \approx 0.7 ， c o s 48^{°} \approx 0.7 ， t a n 48 ° \approx 1 ， 1 ，， s i n 65^{°} \approx 0.9 ， c o s 65^{°} \approx 0.4 ， t a n 65^{°} \approx 2.1$ ）

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的⊙O交 $B C$ 于点D，过点D的直线 $E F$ 交 $A C$ 于点F，交 $A B$ 的延长线于点E，且 $∠ B A C = 2 ∠ B D E$ .

(1)、求证： $D F$ 是⊙O的切线；

(2)、当 $C F = 2 ， B E = 3$ 时，求 $A F$ 的长.

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $C (0 ， 3)$ ，与 $x$ 轴交于点 $A (- 1 ， 0)$ 和点 $B$ （点 $B$ 在点 $A$ 的右边），且 $O B = O C$ .

(1)、求抛物线的解析式和顶点坐标；

(2)、如图1，点 $D$ 、 $E$ 在直线 $x = 1$ 上的两个动点，且 $D E = 1$ ，点 $D$ 在点 $E$ 的上方，求四边形 $A C D E$ 的周长的最小值；

(3)、如图2，点 $P$ 为抛物线上一点，连接 $C P$ ，直线 $C P$ 把四边形 $C B P A$ 的面积分为3：5两部分，求点 $P$ 的坐标.

查看试题解析