新疆阿克苏地区2021年数学中考二模试卷

试卷更新日期：2021-09-18 类型：中考模拟

进入出卷网下载

一、单选题

1. $| - 4 |$ 的相反数是（）

A、4 B、-4 C、 $\frac{1}{4}$ D、 $- \frac{1}{4}$

查看试题解析
2. 如图某个几何图形的三视图，该几何体是（）

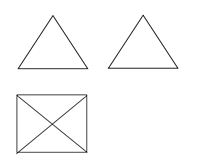A、三棱柱 B、三棱锥 C、四棱锥 D、四棱柱

查看试题解析
3. 下列运算一定正确的是（）.

A、 $2 a + 2 a = 2 a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(2 a^{2})}^{3} = 6 a^{6}$ D、 $(a + b) (a - b) = a^{2} - b^{2}$

查看试题解析
4. 预计到2025年，中国5G用户将超过460000000，将460000000用科学记数法表示为（）

A、4.6×10⁸ B、46×10⁷ C、4.6×10⁹ D、0.46×10⁹

查看试题解析
5. 某校在体育健康测试中，有8名男生“引体向上”的成绩（单位：次）分别是：14，12，8，9，16，10，12，7，这组数据的中位数和众数分别是（）

A、10，12 B、12，11 C、12，12 D、11，12

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x - 3 \leq 5 \\ \frac{x}{3} > 1 \end{array}$ 的整数解有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 暑假期间，某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说，第二次购进的数量比第一次多40套，且两次购书时，每套书的进价相同.若设书店第一次购进该科幻小说x套，由题意列方程正确的是（）

A、 $\frac{600}{x} = \frac{800}{x - 40}$ B、 $\frac{600}{x - 40} = \frac{800}{x}$ C、 $\frac{600}{x} = \frac{800}{x + 40}$ D、 $\frac{600}{x + 40} = \frac{800}{x}$

查看试题解析
8. 将一副三角板 $(∠ A = 30 °)$ 按如图所示方式摆放，若 $A B / / E F$ ，则 $∠ 1$ 等于（）.

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
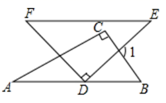9. 如图，二次函数y=ax²+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y₁），若点D（x₂ ， y₂）是抛物线上任意一点，有下列结论：①二次函数y=ax²+bx+c的最小值为﹣4a；②若﹣1≤x₂≤4，则0≤y₂≤5a；③若y₂＞y₁ ，则x₂＞4；④一元二次方程cx²+bx+a=0的两个根为﹣1和 $\frac{1}{3}$ 其中正确结论的个数是（）

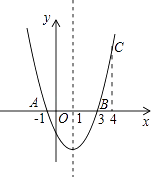A、1 B、2 C、3 D、4

查看试题解析

二、填空题

10. 在函数 $y = \frac{3 x}{2 x - 3}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
11. 分解因式：2a³﹣8a= ．

查看试题解析
12. 在一个不透明的布袋中装有5个红球，2个白球，3个黄球，它们除了颜色外其余都相同，从袋中任意摸出一个球，是黄球的概率为．

查看试题解析
13. 有一人感染了传染性很强的病毒，经过两轮传染后共有625人患病，每轮传染中平均一人传染人.

查看试题解析
14. 如图，点 $P$ 是边长为 $1$ 的菱形 $A B C D$ 对角线 $A C$ 上的一个动点，点 $M ， N$ 分别是 $A B ， B C$ 边上的中点，则 $M P + P N$ 的最小值是.

查看试题解析
15. 如图，在一单位为1的方格纸上， $△ A_{1} A_{2} A_{3} ， △ A_{3} A_{4} A_{5} ， △ A_{5} A_{6} A_{7} \dots \dots$ ，都是斜边在x轴上，斜边长分别为2，4，6，……的等腰直角三角形，若 $A_{1} A_{2} A_{3}$ 的顶点坐标分别为 $A_{1} (2 ， 0) ， A_{2} (1 ， - 1) ， A_{3} (0 ， 0)$ ，则依图中所示规律， $A_{2020}$ 的坐标为.

查看试题解析

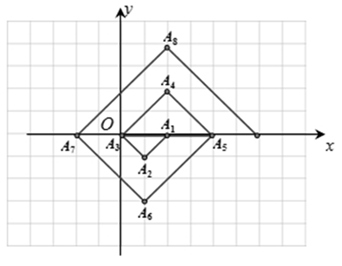
三、解答题

16. 计算： ${(3 - π)}^{0} + 4 \sin 45^{\circ} - \sqrt{8} + | 1 - \sqrt{3} |$ .

查看试题解析
17. 先化简，再求值： $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div (\frac{x - 1}{x + 1} - x + 1)$ ，其中 $x = 2$ .

查看试题解析
18. 已知反比例函数 $y = \frac{k}{x}$ 的图象与一次函数 $y = k x + n$ 的图象交于点 $(2 ， 4)$ .

(1)、分别求出这两个函数的解析式；

(2)、判断 $P (- 1 ， - 20)$ 是否在一次函数 $y = k x + m$ 的图象上并说明原因.

查看试题解析

19. 某课外实践小组的同学们为了解去年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，

月均用水量 $x (t)$	频数（户）	频率
$0 < x \leq 5$	6	0.12
$5 < x \leq 10$	$m$	0.24
$10 < x \leq 15$	16	0.32
$15 < x \leq 20$	10	0.20
$20 < x \leq 25$	4	$n$
$25 < x \leq 30$	2	0.04

解答以下问题：

(1)、表中

m =

，

n =

；

(2)、把频数分布直方图补充完整；

(3)、若该小区有1500户家庭，根据调查数据估计，该小区月均用水量超过

20 t

的家庭大约有多少户？

(4)、若从样本里用水量超过20的家庭中，随机抽取两户，求出“家庭月用水量恰好有一户不多于25”的概率.

查看试题解析

20. 如图，在平行四边形ABCD中，E，F为对角线BD上的两点，且∠DAE＝∠BCF.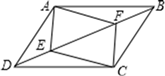

求证：

(1)、AE＝CF；

(2)、四边形AECF是平行四边形.

查看试题解析
21. 在同一直线道路上，小明从学校出发到新华书店，小红从新华书店到学校，小红先出发，图中的折线表示两人之间的距离 $y$ （米）与行走的时间 $t$ （分钟）的函数关系的图象.

(1)、小红的行走速度是多少米/分钟？

(2)、小红与小明相向而行至两人相遇时，求 $y$ （米）与行走的时间 $t$ （分钟）的函数关系？

(3)、两人都到各自目的地时间差多少分钟？

查看试题解析
22. 如图，已知⊙O 的直径 AB 与弦 CD 互相垂直，垂足为点 E.⊙O 的切线 BF 与弦 AC 的延长线相交于点 F，且AC=8，tan∠BDC= $\frac{3}{4}$ .

(1)、求⊙O 的半径长；

(2)、求线段 CF 长.

查看试题解析
23. 如图，抛物线y=ax²+bx+3(a≠0)的对称轴为直线x=-1，抛物线交x轴与点A、C两点，与直线y=x-1交于A、B两点，直线AB与抛物线的对称轴交于点E

(1)、求抛物线的解析式；

(2)、点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标

(3)、在平面直角坐标系中，以点B、E、C、D为顶点的四边形是平行四边形，请直接写出符合条件点D的坐标

查看试题解析