宁夏银川市兴庆区2021年数学中考模拟试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. 下列计算正确的是( )A、7ab﹣5a=2b B、(a+ )2=a2+ C、(﹣3a2b)2=6a4b2 D、3a2b÷b=3a22. 某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A、3,3 B、3,7 C、2,7 D、7,33. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是( )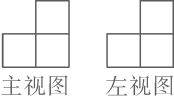 A、6 B、5 C、4 D、34. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、5. 如图,AB CD,AD⊥AC,∠BAD=35°,则∠ACD=( )
A、6 B、5 C、4 D、34. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、5. 如图,AB CD,AD⊥AC,∠BAD=35°,则∠ACD=( ) A、35° B、45° C、55° D、70°6. 如图,四边形 为 的内接四边形,已知 为 ,则 的度数为( )
A、35° B、45° C、55° D、70°6. 如图,四边形 为 的内接四边形,已知 为 ,则 的度数为( ) A、 B、 C、 D、7. 如图, 是平行四边形 的对角线,点 在 上, , ,则 的大小是( )
A、 B、 C、 D、7. 如图, 是平行四边形 的对角线,点 在 上, , ,则 的大小是( )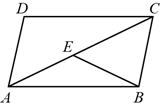 A、 B、 C、 D、8. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、二、填空题
-
9. 分解因式: .10. 在一个不透明的袋子中装有一个白球和一个红球,它们除颜色外均相同,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到白球的概率为.11. 如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为.
 12. 点 和点 在直线 上,则m与n的大小关系是 .13. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),M是OA的中点,点P在BC边上运动.当PO=PM时,点P的坐标为.
12. 点 和点 在直线 上,则m与n的大小关系是 .13. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),M是OA的中点,点P在BC边上运动.当PO=PM时,点P的坐标为.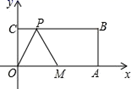 14. 如图,平面直角坐标系xOy中,平行四边形OABC的边OC在 轴上,对角线AC,OB交于点M,函数 ( >0)的图象经过点A(2,4)和点M.则点M的坐标为.
14. 如图,平面直角坐标系xOy中,平行四边形OABC的边OC在 轴上,对角线AC,OB交于点M,函数 ( >0)的图象经过点A(2,4)和点M.则点M的坐标为.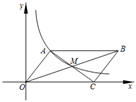 15. 如图,在 中, , , 垂直平分 ,垂足为Q,交 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边 于点D,E;②分别以点D,E为圆心,以大于 的长为半径作弧,两弧相交于点F;⑤作射线 .若 与 的夹角为 ,则 °.
15. 如图,在 中, , , 垂直平分 ,垂足为Q,交 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边 于点D,E;②分别以点D,E为圆心,以大于 的长为半径作弧,两弧相交于点F;⑤作射线 .若 与 的夹角为 ,则 °. 16. 为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行,在 处测得灯塔 在北偏东 方向上,海监船继续向东航行1小时到达 处,此时测得灯塔 在北偏东 方向上. 处到灯塔 的距离是海里.
16. 为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行,在 处测得灯塔 在北偏东 方向上,海监船继续向东航行1小时到达 处,此时测得灯塔 在北偏东 方向上. 处到灯塔 的距离是海里.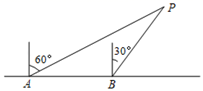
三、解答题
-
17. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
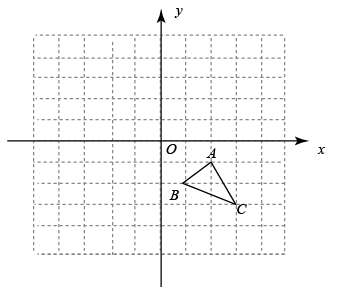
( 1 )请画出与△ABC关于原点O对称的△A1B1C1;
( 2 )请画出△A1B1C1关于y轴对称的△A2B2C2.
18. 解不等式组: .19. 解分式方程: .20. 新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取20人调查学习参与度,数据整理结果如下表:参与度
人数
方式
0.2≤x<0.4
0.4≤x<0.6
0.6≤x<0.8
0.8≤x<1
录播
2
8
6
4
直播
1
5
8
6
(1)、计算接受方式为“录播”的20人的平均参与度和接受方式为“直播”的20人的平均参与度;(2)、从学生接受好的教学方式中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?21. 如图,在菱形 中,点 , 分别是边 , 的中点.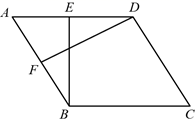 (1)、求证: ;(2)、设 与 的交点为H,若 ,求 的值.22. 某市举办“创建全国文明城市”知识竞赛,已知购买一件甲种奖品和2件乙种奖品共需220元,购买2件甲种奖品和3件乙种奖品共需360元.(1)、求每件甲种奖品和每件乙种奖品的价格分别为多少元?(2)、若计划购买甲种奖品和乙种奖品共30件,总费用不多于2300元,那么最少可购买甲种奖品多少件?23. 如图,点 , , 是半径为2的⊙O上三个点, 为直径, 的平分线交圆于点 ,过点 作 的垂线交 的延长线于点 ,延长 交 的延长线于点 .
(1)、求证: ;(2)、设 与 的交点为H,若 ,求 的值.22. 某市举办“创建全国文明城市”知识竞赛,已知购买一件甲种奖品和2件乙种奖品共需220元,购买2件甲种奖品和3件乙种奖品共需360元.(1)、求每件甲种奖品和每件乙种奖品的价格分别为多少元?(2)、若计划购买甲种奖品和乙种奖品共30件,总费用不多于2300元,那么最少可购买甲种奖品多少件?23. 如图,点 , , 是半径为2的⊙O上三个点, 为直径, 的平分线交圆于点 ,过点 作 的垂线交 的延长线于点 ,延长 交 的延长线于点 .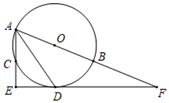 (1)、判断直线 与⊙O的位置关系,并证明.(2)、若 ,求 的值.24. 已知 、 两地之间有一条长240千米的公路.甲车从 地出发匀速开往 地,甲车出发两小时后,乙车从 地出发匀速开往 地,两车同时到达各自的目的地.两车行驶的路程之和 (千米)与甲车行驶的时间 (时)之间的函数关系如图所示.
(1)、判断直线 与⊙O的位置关系,并证明.(2)、若 ,求 的值.24. 已知 、 两地之间有一条长240千米的公路.甲车从 地出发匀速开往 地,甲车出发两小时后,乙车从 地出发匀速开往 地,两车同时到达各自的目的地.两车行驶的路程之和 (千米)与甲车行驶的时间 (时)之间的函数关系如图所示.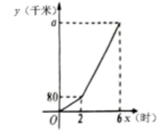 (1)、甲车的速度为千米/时, 的值为.(2)、求乙车出发后, 与 之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.25. 如图,在平面直角坐标系中,点 的坐标是 ,点 为一个动点,过点 作 轴的垂线 ,垂足为 ,点 在运动过程中始终满足 .设平面直角坐标系内点 、 的坐标分别为 , 、 , ,则 ,
(1)、甲车的速度为千米/时, 的值为.(2)、求乙车出发后, 与 之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.25. 如图,在平面直角坐标系中,点 的坐标是 ,点 为一个动点,过点 作 轴的垂线 ,垂足为 ,点 在运动过程中始终满足 .设平面直角坐标系内点 、 的坐标分别为 , 、 , ,则 , (1)、若点 运动到点 时,求CF的值;(2)、设动点 的坐标为 ,求 关于 的函数表达式;(3)、填写下表,并在给定坐标系中画出该函数的图象.
(1)、若点 运动到点 时,求CF的值;(2)、设动点 的坐标为 ,求 关于 的函数表达式;(3)、填写下表,并在给定坐标系中画出该函数的图象.0
2
4
6
8
26. 如图,矩形ABCD中,AB=4,BC=8,P是线段BC上一动点,连接AP并将AP绕P顺时针旋转90°得到线段PE.连接DE,直线DE交BC于F.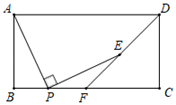 (1)、若BP=1,求PE的长;(2)、设BP=x,四边形APED的面积为S,试求S与x之间的函数关系式;(3)、当x为何值时,四边形APED的面积S最小,并求出最小值.
(1)、若BP=1,求PE的长;(2)、设BP=x,四边形APED的面积为S,试求S与x之间的函数关系式;(3)、当x为何值时,四边形APED的面积S最小,并求出最小值.