江苏省兴化市2021年九年级下学期数学网上阅卷第二次适应性测试试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 如下摆放的几何体中,主视图与左视图有可能不同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如果将一副三角板按如图方式叠放,那么 的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如果将一副三角板按如图方式叠放,那么 的度数是( ) A、 B、 C、 D、5. 某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、 “优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( )
A、 B、 C、 D、5. 某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、 “优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为( ) A、 B、 C、 D、6. 已知关于 的一次函数为 ,那么这个函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、 B、 C、 D、6. 已知关于 的一次函数为 ,那么这个函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
7. 的立方根是 .8. 因式分解: =9. 2021年04月20日,经济日报报道,华为搅动智能汽车“一池春水”.4月17日,北汽新能源旗下品牌极狐联合华为发布了首款Huawei Inside智能纯电轿车北汽阿尔法(华为HI版),该车搭载了华为自动驾驶技术(华为技术已能做到市区1000公里的无人驾驶),其中高版本的售价为429900元.将429900用科学记数法表示为.10. 不等式组 的解集是.11. 命题“如果 ,那么 ”,是(选填“真”或“假”)命题.12. 2021年4月8日,中国扬州世界园艺博览会在扬州仪征市开幕,本届搏览会以“绿色城市,健康生活”为主题.如图,是扬州世界园艺博览会部分导游图,若滩涂印象的坐标为 ,丛林野趣的坐标为 ,则中国馆的坐标为.
 13. 是方程 的一个根,则代数式 的值是.14. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .15. 如图,在扇形 中, ,点 是 的中点,点 , 分别为半径 , 上的动点.若 ,则 周长的最小值为.
13. 是方程 的一个根,则代数式 的值是.14. 若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为 .15. 如图,在扇形 中, ,点 是 的中点,点 , 分别为半径 , 上的动点.若 ,则 周长的最小值为. 16. 如图,在平面直角坐标系 中,点 、 的坐标分别为 、 ,线段 与反比例函数 ( )的图象相交于点 ,以 、 的长为边在线段 的下方构造矩形 ,若矩形 一边的中点在 ( )的图象上,则 的值为.
16. 如图,在平面直角坐标系 中,点 、 的坐标分别为 、 ,线段 与反比例函数 ( )的图象相交于点 ,以 、 的长为边在线段 的下方构造矩形 ,若矩形 一边的中点在 ( )的图象上,则 的值为.
三、解答题
-
17.(1)、计算: .(2)、化简: .18. 第五代移动通信技术(简称 G)是最新一代蜂窝移动通信技术, G移动通信将推动我国数字经济发展迈上新台阶,据预测,2020年到2025年中国 G直接经济产出和间接经济产出的情况如图所示,根据图中提供的信息.
 (1)、2020年到2025年,求 G间接经济产出总量共多少万亿元;(2)、2020年到2025年,求 G间接经济产出总量比直接经济产出总量多多少万亿元;(3)、下面的推断合理的是.(只填序号)
(1)、2020年到2025年,求 G间接经济产出总量共多少万亿元;(2)、2020年到2025年,求 G间接经济产出总量比直接经济产出总量多多少万亿元;(3)、下面的推断合理的是.(只填序号)①2020年到2025年, G间接经济产出和直接经济产出都呈增长趋势.
②2023年到2024年, G间接经济产出和直接经济产出的增长率相同.
19. 嫦娥、神舟、北斗、天问被称为中国航天的“四大天王”.2020年“北斗”组网、“天问”问天、“嫦五”探月,一个个好消息从太空传来,照亮了中国航天界的未来!小玲对航空航天非常感兴趣,她收集到了嫦娥五号、神舟十一号、北斗三号、天问一号的模型图,依次制成编号为A、B、C、D的四张卡片(背面完全相同),将这四张卡片背面朝上,洗匀放好. (1)、小玲从中随机抽取一张卡片是“北斗三号”的概率为;(2)、小玲从四张卡片中随机抽取一张卡片(不放回).再从余下的卡片中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是编号为A(嫦娘五号)和D(天问一号)的概率.20. 如图,在平行四边形 中, 平分 ,已知 , .
(1)、小玲从中随机抽取一张卡片是“北斗三号”的概率为;(2)、小玲从四张卡片中随机抽取一张卡片(不放回).再从余下的卡片中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是编号为A(嫦娘五号)和D(天问一号)的概率.20. 如图,在平行四边形 中, 平分 ,已知 , . (1)、求 的长;(2)、仅用一把无刻度的直尺在 边上确定点 ,使得 .请画出满足题意的点 (保留痕迹,不写作法);21. 如图,一次函数 的图象与 轴的负半轴交于点 ,与 轴的正半轴相交于点 , 的外接圆的圆心为点 .
(1)、求 的长;(2)、仅用一把无刻度的直尺在 边上确定点 ,使得 .请画出满足题意的点 (保留痕迹,不写作法);21. 如图,一次函数 的图象与 轴的负半轴交于点 ,与 轴的正半轴相交于点 , 的外接圆的圆心为点 . (1)、求点 的坐标,并求 的大小;(2)、求图中阴影部分的面积(结果保留根号).22. 平安路上,多“盔”有你.在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶80元,售价为每顶120元,平均每周可售出200顶.商店计划将头盔降价销售,每顶售价不高于108元,经调查发现:每降价1元,平均每周可多售出20顶.(1)、该商店若希望每周获利12000元,则每顶头盔应降价多少元?(2)、当每顶头盔的售价为多少元,商店每周获得最大利润,最大利润是多少?23. 已知,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂 可伸缩( ),且起重臂 可绕点 在一定范围内转动,张角为 ( ),转动点 距离地面 的高度 为 .
(1)、求点 的坐标,并求 的大小;(2)、求图中阴影部分的面积(结果保留根号).22. 平安路上,多“盔”有你.在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶80元,售价为每顶120元,平均每周可售出200顶.商店计划将头盔降价销售,每顶售价不高于108元,经调查发现:每降价1元,平均每周可多售出20顶.(1)、该商店若希望每周获利12000元,则每顶头盔应降价多少元?(2)、当每顶头盔的售价为多少元,商店每周获得最大利润,最大利润是多少?23. 已知,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂 可伸缩( ),且起重臂 可绕点 在一定范围内转动,张角为 ( ),转动点 距离地面 的高度 为 . (1)、当起重臂 长度为 ,张角 为120°时,求云梯消防车最高点 距离地面的高度 ;(2)、某日,一居民家突发险情,该居民家距离地面的高度为 ,请问该消防车能否实施有效救援?(参考数据: )24. 如图, 是⊙O的直径,点 在线段 上,过点 作 交⊙O于点 ,延长 到 , 是⊙O上一动点(不与 、 重合),连接 、 、 ,给出下列信息:①点 为 中点:② ;③ 是 的切线.
(1)、当起重臂 长度为 ,张角 为120°时,求云梯消防车最高点 距离地面的高度 ;(2)、某日,一居民家突发险情,该居民家距离地面的高度为 ,请问该消防车能否实施有效救援?(参考数据: )24. 如图, 是⊙O的直径,点 在线段 上,过点 作 交⊙O于点 ,延长 到 , 是⊙O上一动点(不与 、 重合),连接 、 、 ,给出下列信息:①点 为 中点:② ;③ 是 的切线. (1)、请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个命题.试判断这个命题是否正确,并说明理由.你选择的条件是 ▲ 、 ▲ ,结论是 ▲ (只要填写序号).(2)、在(1)的情况下,若 ,求 的长.25. 如图,已知二次函数 ( )的图象与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,横坐标分别为 , ( )的 、 两点在线段 上(不与 、 重合),过 、 两点作 轴的垂线分别交抛物线于点 、 ,连接 .
(1)、请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个命题.试判断这个命题是否正确,并说明理由.你选择的条件是 ▲ 、 ▲ ,结论是 ▲ (只要填写序号).(2)、在(1)的情况下,若 ,求 的长.25. 如图,已知二次函数 ( )的图象与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,横坐标分别为 , ( )的 、 两点在线段 上(不与 、 重合),过 、 两点作 轴的垂线分别交抛物线于点 、 ,连接 .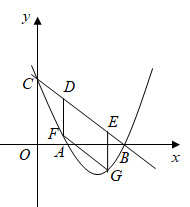 (1)、求线段 的值.(2)、若四边形 是平行四边形;
(1)、求线段 的值.(2)、若四边形 是平行四边形;①点 、 横坐标之和是否为定值,若是定值,请求出;若不是,请说明理由.
②当 时,平行四边形 能否为菱形;若能,求出菱形的周长:若不能,请说明理由.
26. (阅读理解)定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫“协和线”,该四边形叫做“协和四边形”.

(深入探究)
(1)、如图1,在四边形 中, , ,请说明:四边形 是“协和四边形”.(2)、如图2,四边形 是“协和四边形”, 为“协和线”, , ,若点 、 分别为边 、 的中点,连接 , , .求:① 与 的面积的比;
② 的正弦值.
(3)、如图3,在菱形 中, , ,点 、 分别在边 和 上,点 、 分别在边 和 上,点 为 与 的交点,点 在 上,连接 ,若四边形 , 都是“协和四边形”,“协和线”分别是 、 ,求 的最小值.