江苏省无锡市新吴区2021年数学中考二模试卷

试卷更新日期：2021-09-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的绝对值等于（）

A、2 B、-2 C、2或-2 D、 $\frac{1}{2}$

查看试题解析
2. 函数y＝ $\sqrt{2 - x}$ 中自变量x的取值范围是（）

A、x＞2 B、x≤2 C、x≥2 D、x≠2

查看试题解析
3. 下列各式中，与 $x y^{2}$ 是同类项的是（）

A、 $x^{2} y^{2}$ B、 $2 x^{2} y$ C、 $x y$ D、 $- 2 x y^{2}$

查看试题解析
4. 一个多边形的每个内角都等于135°，则这个多边形的边数为（　　）

A、7 B、8 C、9 D、10

查看试题解析
5. P为⊙O内一点， $O P = 3$ ，⊙O半径为5，则经过P点的最短弦长为（）

A、5 B、6 C、8 D、10

查看试题解析
6. 已知一组数据x、y、z的平均数为3，方差为4，那么数据 $x - 2$ ， $y - 2$ ， $z - 2$ 的平均数和方差分别（）

A、1，2 B、1，4 C、3，2 D、3，4

查看试题解析
7. 如图是某几何体的三视图及相关数据，则该几何体的全面积是（）

A、 $10 π$ B、 $15 π$ C、 $20 π$ D、 $24 π$

查看试题解析
8. 如图，正方形 $A B C D$ 的顶点A、D在⊙O上，边 $B C$ 与⊙O相切，若正方形 $A B C D$ 的周长记为 $C_{1}$ ，⊙O的周长记为 $C_{2}$ ，则 $C_{1}$ 、 $C_{2}$ 的大小关系为（）

A、 $C_{1} > C_{2}$ B、 $C_{1} < C_{2}$ C、 $C_{1} = C_{2}$ D、无法判断

查看试题解析
9. 已知：如图，点D是等腰直角△ABC的重心，其中∠ACB=90°，将线段CD绕点C逆时针旋转90°得到线段CE，连结DE，若△ABC的周长为6，则△DCE的周长为（）

A、2 $\sqrt{2}$ B、2 $\sqrt{3}$ C、4 D、3 $\sqrt{2}$

查看试题解析
10. 已知点 $P (- 2 ， y_{1}) ， Q (4 ， y_{2}) ， M (m ， y_{3})$ 均在抛物线 $y = a x^{2} + b x + c$ 上，其中 $2 a m + b = 0$ .若 $y_{3} \geq y_{2} > y_{1}$ ，则m的取值范围是（）

A、 $m < - 2$ B、 $m > 1$ C、 $- 2 < m < 1$ D、 $1 < m < 4$

查看试题解析

二、填空题

11. 因式分解： $m x^{2} - 2 m x + m =$ .

查看试题解析
12. 根据国家卫健委最新数据，截至到2021年4月2日，全国各地累计报告接种新冠病毒疫苗133000000剂次，将133000000用科学记数法表示为.

查看试题解析
13. 在线段、正三角形、平行四边形、矩形、圆中既是轴对称图形又是中心对称图形的个数为.

查看试题解析
14. 某函数的图象不经过第二象限，且经过点（2，1），请写出一个满足上述条件的函数表达式.

查看试题解析
15. 命题“等腰三角形两底角相等”的逆命题是。

查看试题解析
16. 如图，二次函数 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 与一次函数 $y_{2} = m x + n (m \neq 0)$ 的图象相交于点 $A (- 1 ， 5)$ 和 $B (5 ， 2)$ ，则使不等式 $a x^{2} + b x + c < m x + n$ 成立的x的取值范围是.

查看试题解析
17. 如图，菱形 $A B C D$ 中， $∠ A B C = 120 °$ ，顶点 $A ， C$ 在双曲线 $y = \frac{k_{1}}{x} (k_{1} > 0)$ 上，顶点 $B ， D$ 在双曲线 $y = \frac{k_{2}}{x} (k_{2} < 0)$ 上，且 $B D$ 经过点O.若 $k_{1} + k_{2} = 8$ ，则菱形 $A B C D$ 面积的最小值是.

查看试题解析

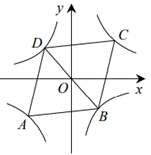
三、解答题

18. 如图， $A B // C D // E F$ ， $A F$ 与 $B E$ 相交于点G，且 $A G ： G D ： D F = 2 ： 1 ： 5$ ，则 $\frac{S_{△ A B G}}{S_{四边形 C E F D}} =$ .

查看试题解析
19.

(1)、计算： ${(\sqrt{3} - π)}^{0} + {(\frac{1}{2})}^{- 2} - 2 \cos 60 °$

(2)、化简： $x (4 x + 3 y) - (2 x + y) (2 x - y)$

查看试题解析
20.

(1)、解方程： $3 x^{2} + x - 4 = 0$

(2)、解不等式组： ${\begin{array}{l} x + 4 \leq 3 (x + 2) ① \\ \frac{x - 1}{2} < \frac{x}{3} ② \end{array}$ ，

查看试题解析
21. 已知：如图，AB∥ED，点F、点C在AD上，AB=DE，AF=DC．求证：BC=EF．

查看试题解析
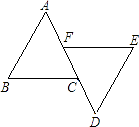22. “安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况，在本校学生中随机抽取部分学生作调查，把收集的数据分为以下4类情形：A.仅学生自己参与；B.家长和学生一起参与；
C.仅家长自己参与； D.家长和学生都未参与.

请根据图中提供的信息，解答下列问题：

(1)、在这次抽样调查中，共调查了名学生；

(2)、补全条形统计图，并在扇形统计图中计算C类所对应扇形的圆心角的度数；

(3)、根据抽样调查结果，估计该校2000名学生中“家长和学生都未参与”的人数.

查看试题解析
23. 现有四位“抗疫”英雄（依次标记为 $A$ 、 $B$ 、 $C$ 、 $D$ ）.为了让同学们了解他们的英雄事迹，张老师设计了如下活动：取四张完全相同的卡片，分别在正面写上 $A$ 、 $B$ 、 $C$ 、 $D$ 四个标号，然后背面朝上放置，搅匀后请一位同学从中随机抽取一张，记下标号后放回，要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.

(1)、班长在这四种卡片中随机抽到标号为 $C$ 的概率为；

(2)、用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.

查看试题解析
24. 如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．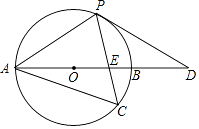

(1)、试判断PD与⊙O的位置关系，并说明理由；

(2)、若点C是弧AB的中点，已知AB=4，求CE•CP的值．

查看试题解析
25. 如图，在 $6 \times 6$ 的正方形网格中，A、B、C、D均为小正方形的顶点，请仅用无刻度的直尺作图，保留作图痕迹.

(1)、在图1中作出 $A C$ 边上的点E，使得 $A E = 3 C E$ ；

(2)、在图2中作出 $B C$ 边上的点F（不与点B重合），使得 $B D = D F$ ；

(3)、在图3中作出 $A B$ 边上的点G，使得 $\tan ∠ A C G = \frac{1}{2}$ .

查看试题解析
26. 一大型商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元件）（x为正整数）之间满足一次函数关系，下表记录的是某三周的有关数据：

x（元/件）

4

5

6

y（件）

10000

9500

9000

(1)、求y与x的函数关系式（不求自变量的取值范围）；

(2)、在销售过程中要求销售单价不低于成本价，且不高于15元/件.若某一周该商品的销售量不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？

(3)、抗疫期间，该商场这种商品售价不大于15元/件时，每销售一件商品便向某慈善机构捐赠m元（ $1 \leq m \leq 6$ ），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.

查看试题解析
27. 已知Rt△ABC中，∠ACB＝90°，CA＝CB＝4，另有一块等腰直角三角板的直角顶点放在C处，CP＝CQ＝2，将三角板CPQ绕点C旋转（保持点P在△ABC内部），连接AP、BP、BQ．

(1)、如图1求证：AP＝BQ；

(2)、如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时，求AP的长；

(3)、设射线AP与射线BQ相交于点E，连接EC，写出旋转过程中EP、EQ、EC之间的数量关系．

查看试题解析
28. 在矩形 $A B C D$ 中，已知 $B C = 9$ ， $A B = 15$ ，E为 $A D$ 上一点，若 $△ A B E$ 沿直线 $B E$ 翻折，使点A落在 $D C$ 边上点F处，折痕为 $B E$ .

(1)、如图1，求证： $△ B C F ∽ △ F D E$ ；

(2)、如图2，矩形 $A B C D$ 的一边 $B C$ 落在平面直角坐标系的x轴上， $C D ⊥ x$ 轴，且点C坐标为 $(n ， 0) (n < 0)$ ，点P为平面内一点，若以O、B、F、P为顶点的四边形是菱形，请直接写出n的值；

(3)、如图3，二次函数的图象经过A、F两点，其顶点为 $M (n - 5 ， h)$ ，连接 $A M$ ，若 $∠ O A M = 90 °$ ，求此二次函数的表达式.

查看试题解析

x（元/件）	4	5	6
y（件）	10000	9500	9000