江苏省泰州市姜堰区2021年数学中考二模试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 第二十四届冬季奥林匹克运动会将于2022年在北京举行,北京将成为历史上第一座既举办过夏奥会,又举办过冬奥会的城市.下面的图形是各届冬奥会会徽中的部分图案,其中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,下面每一组图形都由四个等边三角形组成,其中是正三棱锥展开图的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,下面每一组图形都由四个等边三角形组成,其中是正三棱锥展开图的是( ) A、仅图① B、图①和图② C、图②和图③ D、图①和图③5. 老师组织学生做分组摸球实验.给每组准备了完全相同的实验材料,一个不透明的袋子,袋子中装有除颜色外都相同的3个黄球和若干个白球.先把袋子中的球搅匀后,从中随意摸出一个球,记下球的颜色再放回,即为一次摸球.统计各组实验的结果如下:
A、仅图① B、图①和图② C、图②和图③ D、图①和图③5. 老师组织学生做分组摸球实验.给每组准备了完全相同的实验材料,一个不透明的袋子,袋子中装有除颜色外都相同的3个黄球和若干个白球.先把袋子中的球搅匀后,从中随意摸出一个球,记下球的颜色再放回,即为一次摸球.统计各组实验的结果如下:一组
二组
三组
四组
五组
六组
七组
八组
九组
十组
摸球的次数
100
100
100
100
100
100
100
100
100
100
摸到白球的次数
41
39
40
43
38
39
46
41
42
38
请你估计袋子中白球的个数是( )
A、1个 B、2个 C、3个 D、4个6. 若实数a、b满足 ,则 的值是( )A、1 B、-1 C、3 D、-3二、填空题
-
7. 若分式 有意义,则x的取值范围是.8. “KN95”口罩能过滤空气中95%的直径约为 的非油性颗粒,数据0.0000003用科学记数法表示为.9. 若一组数据1、2、3、4、5的方差是 ,另一组数据101、102、103、104、105的方差是 ,则 (填“>”、“=”或“<”)10. 圆锥的底面半径为 ,母线长为 ,则该圆锥的侧面积是 .11. 若 , 是一元二次方程 的两个根,则 .12. 如图,在 中, ,点D在 边上, 平行 交 于F,若 ,则 的度数为 .
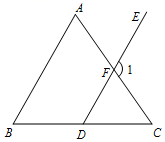 13. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为.
13. 我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离 的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为. 14. 如图,网格中的小正方形边长均为1, 的三个顶点均在网格的格点上,点D、E分别是 、 的中点, 与 交于O,连接 ,则 的长度为.
14. 如图,网格中的小正方形边长均为1, 的三个顶点均在网格的格点上,点D、E分别是 、 的中点, 与 交于O,连接 ,则 的长度为.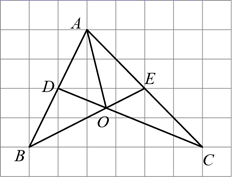 15. 如图,矩形 的顶点B在 上,点A、C在弦 上,且 ,则 .
15. 如图,矩形 的顶点B在 上,点A、C在弦 上,且 ,则 . 16. 如图,在平面直角坐标系 中, ,点P为y轴正半轴上一动点,连接 并延长至点D,使 ,以 为边作 ,连接 ,则 长度的最小值为.
16. 如图,在平面直角坐标系 中, ,点P为y轴正半轴上一动点,连接 并延长至点D,使 ,以 为边作 ,连接 ,则 长度的最小值为.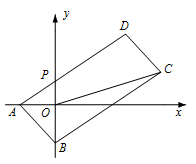
三、解答题
-
17.(1)、计算: ;(2)、解方程: .18. 某校为了了解九年级学生的心理健康状况,随机抽取了九年级部分学生进行测试,测试满分为100分,发现所有参测学生成绩均超过60分,将本次测试成绩绘制成如下频数分布表:
等次
分数段
频数
频率
A
8
c
B
a
d
C
92
0.46
D
b
0.30
请根据统计表回答下列问题:
(1)、 , ;(2)、若用扇形统计图表示统计结果,B等次对应的圆心角的度数为 ;(3)、该校某同学说:“根据测试成绩可以估计我校约有30%的学生心理健康状况属于D等次”,他的说法正确吗?请说明理由.19. 如图,有A、B、C三个相邻的座位,甲、乙、丙三名同学等可能地坐到这3个座位上. (1)、甲同学坐在A座位的概率为;(2)、用画树状图或列表的方法求出乙、丙两同学恰好相邻而坐的概率.20. 某厂生产甲、乙两种型号的产品,生产1个甲种产品需要用时2分钟、耗材30克;生产1个乙种产品需要用时3分钟、耗材40克.如果生产甲产品和生产乙产品共用时 小时、耗材11千克,那么甲、乙两种产品各生产多少个?21. 如图,在 中, .
(1)、甲同学坐在A座位的概率为;(2)、用画树状图或列表的方法求出乙、丙两同学恰好相邻而坐的概率.20. 某厂生产甲、乙两种型号的产品,生产1个甲种产品需要用时2分钟、耗材30克;生产1个乙种产品需要用时3分钟、耗材40克.如果生产甲产品和生产乙产品共用时 小时、耗材11千克,那么甲、乙两种产品各生产多少个?21. 如图,在 中, .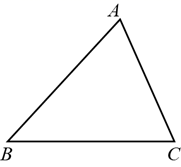 (1)、在平面内求作点D,使D到直线 、 的距离相等,且 ,请用直尺和圆规作出符合条件的点D(保留作图痕迹,不需写出作法);(2)、在(1)的条件下,求以A、B、C、D为顶点构成的四边形的周长.22. 如图,一次函数 的图象与x轴交于点A,与反比例函数 的图象交于点B,过点B作 轴于C,点D在该反比例函数的图象上,点D在点B的右侧.
(1)、在平面内求作点D,使D到直线 、 的距离相等,且 ,请用直尺和圆规作出符合条件的点D(保留作图痕迹,不需写出作法);(2)、在(1)的条件下,求以A、B、C、D为顶点构成的四边形的周长.22. 如图,一次函数 的图象与x轴交于点A,与反比例函数 的图象交于点B,过点B作 轴于C,点D在该反比例函数的图象上,点D在点B的右侧.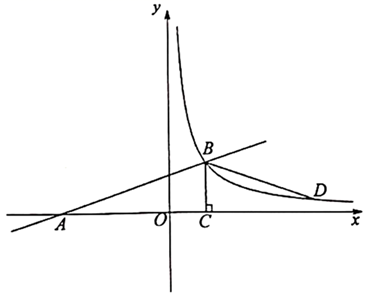
请从以下三个选项中选择两个作为已知条件,剩下一个作为结论,并写出结论成立的计算或证明的过程.① ;② ;③ .
你选择的条件是 ▲ ,结论是 ▲ .(填序号)
23. 如图,一架无人机静止悬浮在空中P处,小明在山坡A处测得无人机的仰角为 ,小亮在水平地面C处测得无人机的仰角为 ,已知山坡 的坡度 ,斜坡 长为52米,水平地面 长为62米,求此时无人机离地面的高度 的长.(参考数据: )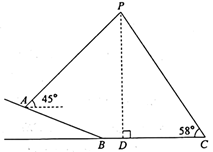 24. 如图, 为 的直径,弦 于E, ,交 的延长线于F, .
24. 如图, 为 的直径,弦 于E, ,交 的延长线于F, . (1)、求证: 为 的切线;(2)、若 ,求 、 、弧 围成的阴影部分的面积.25. 阅读理解:
(1)、求证: 为 的切线;(2)、若 ,求 、 、弧 围成的阴影部分的面积.25. 阅读理解:如果一个等腰三角形的三个顶点在矩形的边上或矩形的边所在的直线上,我们称这个等腰三角形为这个矩形的“友好三角形”.
解决问题:
如图,在矩形 中, 是对角线,点E为直线 上的一个动点,过点E作 平行 交 或 于F,连接 、 .
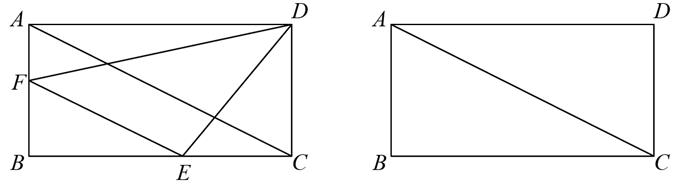 (1)、若点E在边 上,且 ,以下三角形:① ② ③ ④ ,其中为矩形 的“友好三角形”的是(填序号);(2)、当 时,试判断 是否为矩形 的“友好三角形”?请说明理由;(3)、当 为矩形 的“友好三角形”时,求 的长.26. 在平面直角坐标系 中,点 、 是二次函数 图象上的两个点.(1)、当 时,求该二次函数图象与x轴的交点坐标:(2)、当 时,
(1)、若点E在边 上,且 ,以下三角形:① ② ③ ④ ,其中为矩形 的“友好三角形”的是(填序号);(2)、当 时,试判断 是否为矩形 的“友好三角形”?请说明理由;(3)、当 为矩形 的“友好三角形”时,求 的长.26. 在平面直角坐标系 中,点 、 是二次函数 图象上的两个点.(1)、当 时,求该二次函数图象与x轴的交点坐标:(2)、当 时,①判断 的值是否随着a的变化而变化?若不变,求 的值;若变化,说明理由;
②若 ,求t的值;
(3)、若 ,且 ,求出所有符合条件的正整数m的值;