江苏省南京玄武区2021年数学中考二模试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. 化简 的正确结果是( )A、4 B、±4 C、 D、2. 计算 的结果是( )A、 B、 C、 D、3. 下列图形中,是圆锥的侧面展开图的为( )A、
 B、
B、 C、
C、 D、
D、 4. 下列整数中,与 最接近的是( )A、3 B、4 C、5 D、65. 已知二次函数 ( 为常数, )当 时, ,则该函数图象的顶点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 某聊天软件规定:若任意连续5天,好友双方的每日聊天记录的条数不低于100,则双方可以获得“星形”标识.甲、乙两位好友连续5天在该软件上聊天,下面是这5天日聊天记录条数的统计量,一定能判断甲、乙获得“星形”标识的是( )A、中位数为110条,极差为20条 B、中位数为110条,众数为112条 C、中位数为106条,平均数为102条 D、平均数为110条,方差为10条2
4. 下列整数中,与 最接近的是( )A、3 B、4 C、5 D、65. 已知二次函数 ( 为常数, )当 时, ,则该函数图象的顶点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 某聊天软件规定:若任意连续5天,好友双方的每日聊天记录的条数不低于100,则双方可以获得“星形”标识.甲、乙两位好友连续5天在该软件上聊天,下面是这5天日聊天记录条数的统计量,一定能判断甲、乙获得“星形”标识的是( )A、中位数为110条,极差为20条 B、中位数为110条,众数为112条 C、中位数为106条,平均数为102条 D、平均数为110条,方差为10条2二、填空题
-
7. 写出一个负数,使这个数的绝对值大于2:.8. 若式子 在实数范围内有意义,则x的取值范围是 .
9. 计算 的结果是.10. 分解因式 的结果是.11. 纳米 是非常小的长度单位, ,我国某物理研究所已研制出直径为 的碳纳米管,用科学记数法表示 是 .12. 如图是一个正六边形的飞镖游戏板,顺次连接三个不相邻的顶点将正六边形分成4个区域.向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影区域的概率是. 13. 如图, 、 分别是反比例函数 , 图象上的点,且 轴, 是 轴上的点,连接 , .若 的面积是3,则 的值是.
13. 如图, 、 分别是反比例函数 , 图象上的点,且 轴, 是 轴上的点,连接 , .若 的面积是3,则 的值是. 14. 如图,在 中, , 的垂直平分线 交 边于点 ,垂足为 ,若 , ,则 的长为.
14. 如图,在 中, , 的垂直平分线 交 边于点 ,垂足为 ,若 , ,则 的长为. 15. 如图,直线 经过正五边形 的中心 ,与 、 边分别交于点 、 ,点 是点 关于直线 的对称点,连接 , ,则 的度数为°.
15. 如图,直线 经过正五边形 的中心 ,与 、 边分别交于点 、 ,点 是点 关于直线 的对称点,连接 , ,则 的度数为°. 16. , 是下列函数图象上任意的两点:① ;② ;③ ;④ ;其中,满足 的函数有.(填上所有正确的序号)
16. , 是下列函数图象上任意的两点:① ;② ;③ ;④ ;其中,满足 的函数有.(填上所有正确的序号)三、解答题
-
17. 解下列方程.(1)、 ;(2)、 .18. 先化简,再求值: ,其中 .19. 一个家具厂有甲、乙两个木料供货商,随机抽取该家具厂向这两个供货商订货后等待交货天数的样本数据,样本容量都为 10,并绘制如下统计图.
 (1)、扇形统计图中“9天”对应扇形的圆心角度数为°;(2)、根据以上信息,填空:
(1)、扇形统计图中“9天”对应扇形的圆心角度数为°;(2)、根据以上信息,填空:供货商
平均数/天
中位数/天
众数/天
方差/天2
甲
①
②
9
1.8
乙
8
8
8
③
(3)、你认为家具厂从哪一个供货商进货比较好?请说明理由.20. 如图,在 和 中, , , .求证 . 21. 某学校护学岗值班,每天只需要一名家长.甲、乙两位家长从周一到周四这四天中各随机选择两天值班.(1)、求甲恰好是连续的两天值班的概率;(2)、甲、乙恰好都是连续的两天值班的概率是.22. 如图,某海域有两个海岛 , ,海岛 位于海岛 的正南方向,这两个海岛之间有暗礁,灯塔 位于海岛 的南偏东47.5°方向,海岛 的北偏东70°方向,一艘海轮从海岛 出发,沿正南方向航行32海里到达 处,测得灯塔 在北偏东37°方向上.求海岛 , 之间的距离.(参考数据: , , )
21. 某学校护学岗值班,每天只需要一名家长.甲、乙两位家长从周一到周四这四天中各随机选择两天值班.(1)、求甲恰好是连续的两天值班的概率;(2)、甲、乙恰好都是连续的两天值班的概率是.22. 如图,某海域有两个海岛 , ,海岛 位于海岛 的正南方向,这两个海岛之间有暗礁,灯塔 位于海岛 的南偏东47.5°方向,海岛 的北偏东70°方向,一艘海轮从海岛 出发,沿正南方向航行32海里到达 处,测得灯塔 在北偏东37°方向上.求海岛 , 之间的距离.(参考数据: , , )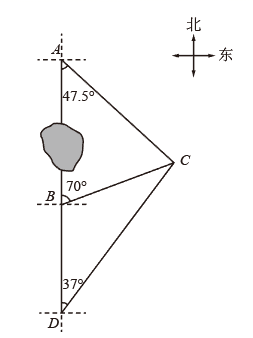 23. 如图,在 中, , 分别是 , 边上的点, ,连接 . , 的平分线分别交 , 边于点 , ,连接 , .
23. 如图,在 中, , 分别是 , 边上的点, ,连接 . , 的平分线分别交 , 边于点 , ,连接 , . (1)、求证:四边形 是平行四边形;(2)、小明在完成(1)的证明后继续探索,他猜想:当 为 的中点时,四边形 是矩形,请在下列框图中补全他的证明思路.
(1)、求证:四边形 是平行四边形;(2)、小明在完成(1)的证明后继续探索,他猜想:当 为 的中点时,四边形 是矩形,请在下列框图中补全他的证明思路.小明的证明思路
连接 .由(1)知四边形 是平行四边形.要证 是矩形,只要证 .
故只要证 .
由已知条件( ),故只要证 ,
即证四边形 为平行四边形.易证( )
故只要证 ,易证 ,故只要证( ), 易证 ,即可得证.
24. 已知二次函数 ( 是常数).(1)、求证:不论 为何值,该二次函数图象与 轴总有两个公共点;(2)、二次函数的图象与 轴交于点 ,顶点为 ,将二次函数的图象沿 轴翻折,所得图象的顶点为 ,若 是等边三角形,求 的值.25. 小明在动物园游玩结束后,联系爸爸去餐厅就餐,如图①,小明从动物园骑车出发,匀速前往餐厅.稍后,小明爸爸从家开车出发,匀速前往餐厅;行驶一段时间, 爸爸发现手机落在家里,立即按原路以原速返回(取手机的时间忽略不计),再立即以原速前往餐厅,设小明出发第 时,与餐厅的距离为 ,小明爸爸与餐厅的距离为 . , 与 之间的函数关系如图②所示. (1)、小明的速度是 ;(2)、求线段 所表示的 与 之间的函数表达式;(3)、设小明与爸爸之间的距离为 ,在图③中画出 与 之间的函数图象.(标明必要的数据)26. 在 中, , ,经过 , 的 与 边另一个公共点为 ,与 边另一个公共点为 ,连接 .
(1)、小明的速度是 ;(2)、求线段 所表示的 与 之间的函数表达式;(3)、设小明与爸爸之间的距离为 ,在图③中画出 与 之间的函数图象.(标明必要的数据)26. 在 中, , ,经过 , 的 与 边另一个公共点为 ,与 边另一个公共点为 ,连接 . (1)、如图①,若 , ,求 的半径;(2)、如图②,作 ,交 边于点 .求证:直线 与 相切.27. (问题情境)
(1)、如图①,若 , ,求 的半径;(2)、如图②,作 ,交 边于点 .求证:直线 与 相切.27. (问题情境)如图①,小区 、 位于一条笔直的道路 的同侧,为了方便 , 两个小区居民投放垃圾,现在 上建一个垃圾分类站 ,使得 与 , 的距离之比为 .
 (1)、(初步研究)
(1)、(初步研究)
在线段 上作出点 ,使 .如图,做法如下:

第一步:过点 作射线 ,
以 为圆心,任意长为半径画弧,交 于点 ;
以 为圆心, 长为半径画弧,交 于点 ;
以 为圆心, 长为半径画弧,交 于点 .
第二步:连接 ,作 ,交 于点 .
则点 即为所求.
请证明所作的点 满足 .
(2)、(深入思考)
如图,点 在线段 上,点 在直线 外,且 .求证: 是 的平分线.
 (3)、(问题解决)
(3)、(问题解决)
如图,已知点 , 和直线 ,点 在线段 上,且 .用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(ⅰ)在直线 上作出点 (异于点 ),使 ;
(ⅱ)在直线 上作出点 ,使 .
