江苏省南京市秦淮区2021年数学中考二模试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 计算 的结果是( )A、 B、 C、 D、3. 数轴上表示 两数的点分别在原点左、右两侧,下列事件是随机事件的是( )A、 B、 C、 D、4. 如图,过反比例函数 的图象上的一点P作 轴,垂足为Q,连接 .若 的面积是2,则k的值是( )
 A、4 B、-4 C、2 D、-25. 用一个平面截棱长为1的正方体(如图),截面形状不可能是( )
A、4 B、-4 C、2 D、-25. 用一个平面截棱长为1的正方体(如图),截面形状不可能是( )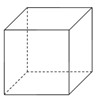 A、边长为1的正方形 B、长为 、宽为1的矩形 C、边长为 的正三角形 D、三边长为1、1、 的三角形6. 百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形 (如图),以下结论:
A、边长为1的正方形 B、长为 、宽为1的矩形 C、边长为 的正三角形 D、三边长为1、1、 的三角形6. 百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形 (如图),以下结论:① ;②若 ,则 ;③若 ,则 ;④存在凹四边形 ,有 .其中所有正确结论的序号是( )
 A、①② B、①②③ C、①②④ D、①③④
A、①② B、①②③ C、①②④ D、①③④二、填空题
-
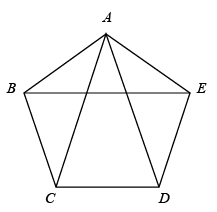
7. 若式子 在实数范围内有意义,则x的取值范围是.8. 计算 的结果是.9. 新冠病毒粒径约为 ,用科学记数法表示 是m.10. 若 是一元二次方程 的两个根,则 的值是.11. 顶角是 的等腰三角形叫做黄金三角形.如图, 是正五边形 的3条对角线,图中黄金三角形的个数是.
 12. 如图,在 中, .将 绕点C顺时针旋转后得 ,且点 落在 边上,连接 .若 ,则四边形 的面积为.
12. 如图,在 中, .将 绕点C顺时针旋转后得 ,且点 落在 边上,连接 .若 ,则四边形 的面积为.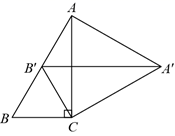 13. 已知四边形 的四个顶点都在 上,则得到结论 .上述推理由因到果的依据是.14. 将二次函数 的图象沿着y轴翻折,所得到的图象对应的函数表达式是.15. 如图,线段 的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则 的值是.
13. 已知四边形 的四个顶点都在 上,则得到结论 .上述推理由因到果的依据是.14. 将二次函数 的图象沿着y轴翻折,所得到的图象对应的函数表达式是.15. 如图,线段 的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则 的值是. 16. 在平面直角坐标系 中,以O为圆心,2个单位长度为半径画圆.若一次函数 (k为常数, )的图象与 有公共点,则k的取值范围是.
16. 在平面直角坐标系 中,以O为圆心,2个单位长度为半径画圆.若一次函数 (k为常数, )的图象与 有公共点,则k的取值范围是.三、解答题
-
17. 解方程组18. 解一元一次不等式 ,并把它的解集在数轴上表示出来.
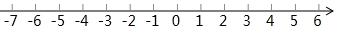 19. 已知甲做60个零件所用的时间与乙做90个零件所用的时间相等.若乙比甲每小时多做9个零件,则甲、乙两人每小时各做多少个零件?20. 某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
19. 已知甲做60个零件所用的时间与乙做90个零件所用的时间相等.若乙比甲每小时多做9个零件,则甲、乙两人每小时各做多少个零件?20. 某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).
甲、乙两人连续8次射击成绩统计表
平均成绩(环)
中位数(环)
方差( )
甲
▲
7.5
▲
乙
6
▲
3.5
(1)、补全统计图和统计表;(2)、如果你是教练,要从甲、乙两人中选一位参加比赛,你会选谁?写出你这样选择的2条理由.21. 在4张完全一样的纸条上分别写上 ,做成4支签,放入一个不透明的盒子中搅匀.甲先从中任意抽出1支签,不放回,乙再从剩余的签中任意抽出1支.(1)、甲抽到写着数字“1”的签的概率是.(2)、乙抽到写着数字“1”的签的概率与(1)的结果相同吗?请通过计算说明.22. 如图,在 中, 是 的中点,过点D作 且 ,交 于点O,连接 .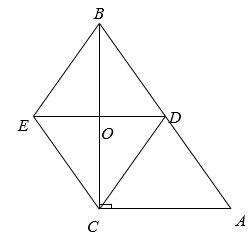 (1)、求证:四边形 是菱形;(2)、当 和 满足数量关系时,四边形 是正方形.23. 如图, 的弦 相交于点P,且 .求证 .
(1)、求证:四边形 是菱形;(2)、当 和 满足数量关系时,四边形 是正方形.23. 如图, 的弦 相交于点P,且 .求证 .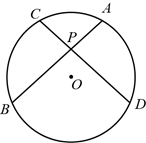 24. 如图,有一垂直于地面的电线杆 .在一建筑物二楼平台上的C处和三楼平台上的D处测得A的仰角分别为 .已知建筑物的层高 和 都是 的长为 .求电线杆 的高度.(图中所有点都在同一平面内,参考数据: .)
24. 如图,有一垂直于地面的电线杆 .在一建筑物二楼平台上的C处和三楼平台上的D处测得A的仰角分别为 .已知建筑物的层高 和 都是 的长为 .求电线杆 的高度.(图中所有点都在同一平面内,参考数据: .)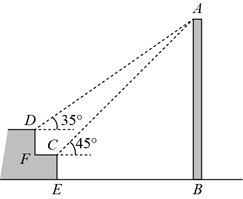 25. 如图,在 中,E是 上一点,延长 到点F,使 .
25. 如图,在 中,E是 上一点,延长 到点F,使 .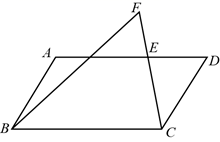 (1)、求证 ;(2)、用直尺和圆规在 上作出一点P,使 (保留作图的痕迹,不写作法).26. 如图①,小明和小亮分别站在平地上的 两地先后竖直向上抛小球 (抛出前两小球在同一水平面上),小球到达最高点后会自由竖直下落到地面. 两球到地面的距离 和 与小球A离开小明手掌后运动的时间 之间的函数图象分别是图②中的抛物线 .已知抛物线 经过点 ,顶点是 ,抛物线 经过 和 两点,两抛物线的开口大小相同.
(1)、求证 ;(2)、用直尺和圆规在 上作出一点P,使 (保留作图的痕迹,不写作法).26. 如图①,小明和小亮分别站在平地上的 两地先后竖直向上抛小球 (抛出前两小球在同一水平面上),小球到达最高点后会自由竖直下落到地面. 两球到地面的距离 和 与小球A离开小明手掌后运动的时间 之间的函数图象分别是图②中的抛物线 .已知抛物线 经过点 ,顶点是 ,抛物线 经过 和 两点,两抛物线的开口大小相同. (1)、分别求出 与x之间的函数表达式.(2)、在小球B离开小亮手掌到小球A落到地面的过程中.
(1)、分别求出 与x之间的函数表达式.(2)、在小球B离开小亮手掌到小球A落到地面的过程中.①当x的值为 ▲ 时,两小球到地面的距离相等;
②当x为何值时,两小球到地面的距离之差最大?最大是多少?
27. 如图,E是边长为4的正方形 边 上一点, 长为1.点F从点B开始,在正方形的边上,沿着 方向运动,到达点C后停止运动.点A关于直线 的对称点为 .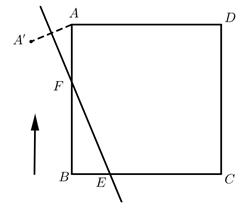 (1)、【从“点”开始】
(1)、【从“点”开始】
求点 与点D的最小距离和最大距离.(2)、【由“点”到“线”】
当直线 与点 的轨迹(即点 运动形成的图形)有且只有1个公共点时, 的长是.(3)、【拓“线”成“形”】
在点F经过点A后至点F到达点C前的过程中,当点 恰好落在正方形 的边所在直线上时,直接写出此时点F运动的路程.