江苏省南京市联合体2021年数学中考二模试卷

试卷更新日期：2021-09-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个实数中，是负数的是（）

A、－（－1） B、（－1）² C、|－1| D、（－1）³

查看试题解析
2. 计算（－a²）³÷a²的结果是

A、－a⁴ B、－a³ C、a⁴ D、a³

查看试题解析
3. 下列整数中，与 $7 - \sqrt{15}$ 最接近的是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 若将一组数据中的每个数都加3，那么所得的这组新数据（）

A、平均数不变 B、中位数不变 C、众数不变 D、方差不变

查看试题解析
5. 如图，一次函数y＝－x＋6的图象与反比例函数 $y = \frac{k}{x}$ （k为常数，k≠0）的图象交于点A、B，若AB＝ $4 \sqrt{2}$ ，则k的值是（）

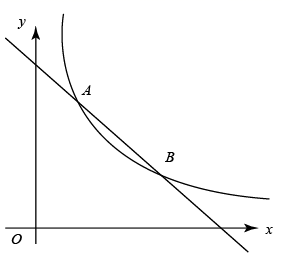A、3 B、4 C、5 D、6

查看试题解析
6. 如图，在等腰△ABC中，AB＝AC，D、E分别在BC、AC上，AD＝DE，BD＝CE，若∠ADE＝m°，则∠BAD的度数是（）

A、m° B、 $(90 - \frac{1}{2} m)$ ° C、（90－m）° D、 $(90 - \frac{3}{2} m)$ °

查看试题解析

二、填空题

7. 计算： $| - 3 | =$ ； $\sqrt{{(- 3)}^{2}} =$ .

查看试题解析
8. 习近平总书记在全国脱贫攻坚总结表彰大会上宣告现行标准下98 990 000农村贫困人口全部脱贫.用科学记数法表示98 990 000是.

查看试题解析
9. 计算 $\frac{\sqrt{12} - \sqrt{27}}{\sqrt{3}}$ ＝.

查看试题解析
10. 方程组 ${\begin{array}{l} x - 2 y = 3 \\ 2 x - y = 9 \end{array}$ 的解是.

查看试题解析
11. 设x₁ ， x₂是一元二次方程x²－3x－4＝0的两个根，则x₁x₂－x₁－x₂＝.

查看试题解析
12. 分解因式x³－2x²＋x的结果是.

查看试题解析
13. 如图，四边形ABCD是⊙O的内接四边形，∠A：∠C＝2：3，若⊙O半径为5，则 $\overset{⌢}{B D}$ 的长度是.

查看试题解析
14. 如图，正五边形ABCDE的边长为2，对角线BD、CE相交于点F，则DF·BD的值为.

查看试题解析
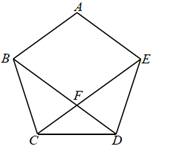15. 如图，在△ABC中，点E在BC上，且BE＝3EC.D是AC的中点，AE、BD交于点F，则 $\frac{A F}{E F}$ 的值为.

查看试题解析
16. 已知一次函数y＝ $\frac{1}{2}$ x＋1的图象与y轴交于点A，将该函数图象绕点A旋转45°，旋转后的图象对应的函数关系式是.

查看试题解析

三、解答题

17. 计算 $(a - 1 - \frac{3}{a + 1}) \div \frac{a^{2} - 4}{a^{2} + 2 a + 1}$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} 4 - 3 x ⩾ - 5 \\ \frac{2 x - 1}{3} > \frac{x - 2}{2} \end{array}$ 并写出该不等式组的最小整数解.

查看试题解析
19. 3月14日是国际数学日，“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣，某校开展了一次数学趣味知识竞赛（竞赛成绩为百分制），并随机抽取了50名学生的竞赛成绩（本次竞赛没有满分），经过整理数据得到以下信息：
信息一：50名学生竞赛成绩频数分布直方图如图所示，从左到右依次为第一组到第五组（每组数据含前端点值，不含后端点值）.

信息二：第三组的成绩（单位：分）为74 71 73 74 79 76 77 76 76 73 72 75

根据信息解答下列问题：

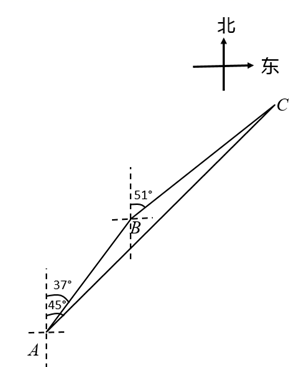
(1)、补全第二组频数分布直方图（直接在图中补全）；

(2)、第三组竞赛成绩的众数是分，抽取的50名学生竞赛成绩的中位数是分；

(3)、若该校共有1500名学生参赛，请估计该校参赛学生成绩不低于80分的约为人.

查看试题解析
20. 某阅读网站现开通了A、B、C、D这4本书的免费下载权限，每位用户可免费下载其中2本阅读.

(1)、求甲用户选择下载的2本书是A、B的概率；

(2)、甲、乙两个用户选择下载的2本书均不相同的概率是.

查看试题解析
21. 某车间加工1800个零件后，采用了新工艺，工作效率是原来的1.2倍，这样加工同样个数的零件就少用了15h，求采用新工艺前后每小时各加工多少个零件？

查看试题解析
22. 如图，在 $▱$ ABCD中，点E、F在对角线BD上，BE＝DF.

(1)、求证：四边形AECF是平行四边形；

(2)、若BD平分∠ABC，求证：四边形AECF是菱形.

查看试题解析
23. 如图，港口B位于港口A北偏东37°的方向，两港口距离为30海里.在港口A处测得一艘军舰在北偏东45°方向的C处，在港口B处测得该军舰在北偏东51°方向.求该军舰距港口B的距离BC.（结果保留整数）
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin51°≈0.78，cos51°≈0.63，tan51°≈1.25）

查看试题解析
24. 已知二次函数y＝ax²－4ax＋3a（a为常数，且a≠0）

(1)、求证：不论a为何值，该函数的图象与x轴总有两个公共点.

(2)、当1≤x≤4时，y＜5，直接写出a的取值范围.

查看试题解析
25. 如图，在矩形ABCD中，AB＝9，BC＝8，⊙O过点A且与BC相切于点E.设BE＝m.

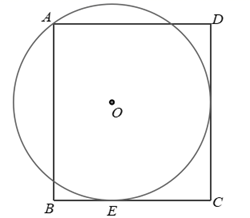(1)、当⊙O与CD相切时，求m的值；

(2)、点E从B向C运动，⊙O与CD边公共点的个数随m的变化而变化.直接写出公共点的个数及其对应的m的取值范围；

(3)、在点E从B向C运动的过程中，画出点O的运动路径，这个路径是.（填写序号）

①线段；

②弧；

③双曲线的一部分；

④抛物线的一部分

查看试题解析
26. 某商品有线上、线下两种销售方式.
线上销售单件利润定为600元时，销售量为0件，单件利润每减少1元销售量增加1件.另需支付其它成本5 000元；线下销售单件利润500元.另需支付其它成本12 500元.(注：净利润＝销售商品的利润－其他成本)

(1)、线上销售100件的净利润为元；线下销售100件的净利润为元；

(2)、若销售量为x件，当0＜x≤600时，比较两种销售方式的净利润；

(3)、现有该商品400件，若线上、线下同时销售，售完后的最大净利润是多少元？此时线上、线下各销售多少件？

查看试题解析
27. 如图

(1)、如图①，AB＝AC，点P为BC上一点，∠BAP＝30°，∠PAC＝45°.求 $\frac{B P}{C P}$ 的值；

(2)、如图②，AB＝AC，DB＝DC，点P为BC上一点，求证 $\frac{\sin ∠ B A P}{\sin ∠ B D P} = \frac{\sin ∠ C A P}{\sin ∠ C D P}$ ；

(3)、如图③，⊙O是△ABC的内切圆，切点分别为D、E、F，连接EF、DO相交于点I，连接AI并延长交BC于点G. 求证BG＝CG.

查看试题解析