江苏省南京鼓楼区2021年数学中考二模试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. 比-3小2的数是( )A、-5 B、-1 C、1 D、52. 下列计算中,结果正确的是( )A、 B、 C、 D、3. 如果一个多边形的每个外角都是36°,那么这个多边形的边数是( )A、5 B、6 C、10 D、124. 在平面直角坐标系中,将一次函数 的图象向左平移1个单位长度,得到的图象对应的函数表达式是( )A、 B、 C、 D、5. 正比例函数 和反比例函数 的图象如图所示,交点 的坐标是 ,那么当 时, 的取值范围是( )
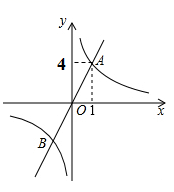 A、 B、 C、 D、 或6. 如图, 中, , , ,点 从 点出发,沿 运动到点 停止,过点 作射线 的垂线,垂足为 ,点 运动的路径长为( )
A、 B、 C、 D、 或6. 如图, 中, , , ,点 从 点出发,沿 运动到点 停止,过点 作射线 的垂线,垂足为 ,点 运动的路径长为( )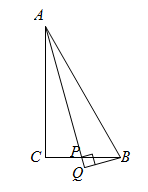 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
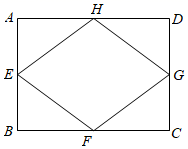
7. 如果反比例函数 的图象经过点 那么也经过点( ,).8. 若8的平方根和立方根分别是 和 ,则 .9. 若 ,则代数式 的值是.10. 若式子 在实数范围内有意义,则 的取值范围是.11. 如图,矩形 中, , ,顺次连接 、 、 、 的中点得到四边形 ,那么四边形 的面积为.
 12. 若一组数据2,3,4,5, 的方差是2,那么 的值为.13. 将一副三角板如图摆放,则 °.
12. 若一组数据2,3,4,5, 的方差是2,那么 的值为.13. 将一副三角板如图摆放,则 °.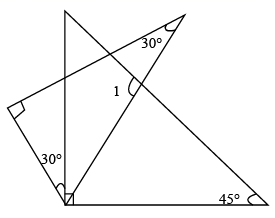 14. 如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为.
14. 如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为.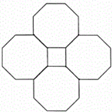 15. 如图,在四边形 中, , ,在 、 上分别取一点 、 ,使 的周长最小,则 °.
15. 如图,在四边形 中, , ,在 、 上分别取一点 、 ,使 的周长最小,则 °.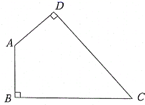
三、解答题
-
16. 解不等式组 ,并写出它的整数解.17. 某同学解方程 ,过程如下:
第一步:整理,得 ,
第二步:……
(1)、请你说明第一步变化过程的依据是:;(2)、请把以上解方程的过程补充完整.18. 某新冠疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其中有两箱储存 厂家的疫苗,另两箱分别储存 厂家和 厂家的疫苗.(1)、如果从中随机拿出两个箱子,送往1号和2号接种台,求拿出的两个冷藏箱里有 厂家疫苗的概率;(2)、如果将4个箱子随机送往4个接种台,每个接种台接受一个箱子,那么1号台恰好拿到 厂家疫苗的概率是.19. 某学校七、八、九年级分别有1000、1200和1400名学生,为了了解学生对校服的满意度,随机抽取七、八年级各100名学生,九年级200名学生,进行综合评价(打分为整数,满分100分),下面给出了一些信息.信息一:七年级打分成绩的频数分布表:
分组
人数
6
16
18
28
32
信息二:七年级学生打分在 这一组的分数统计表:
分数
80
81
82
83
84
85
86
87
88
89
人数
2
3
1
0
2
2
6
2
7
3
信息三:九年级学生打分的统计表:
分数
62
63
64
66
67
68
69
71
72
73
74
76
77
78
人数
1
2
1
2
3
1
4
4
3
9
1
1
3
3
分数
80
81
82
83
84
86
88
89
90
92
93
95
96
98
人数
5
17
9
15
20
18
16
12
20
10
4
5
5
6
信息四:三个年级打分成绩的平均数、中位数、众数如下表:
年级
平均数
中位数
众数
七年级
82
88
八年级
86
84.5
86
九年级
84
(1)、表中 ; ; ;(2)、此次调查中,满意度较高的是哪一个年级,请说明理由;(3)、如果全校3600名学生全部参与打分,你估计打分在85分以上(含85分)的约有多少人?20. 已知 , .按下列要求用直尺和圆规作图.(保留作图痕迹,不写作法)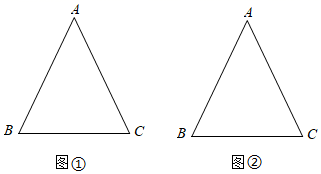 (1)、在图①中求作一点 ,使 ,且 、 在直线 异侧;(2)、在图②中求作一点 ,使 ,且 、 在直线 同侧.21. 小明写完作业后到图书馆找妈妈一起看书.小明从家出发,走了一段路程后突然发现钥匙与图书证忘带,立即打电话给妈妈(打电话时间忽略不计).妈妈立即骑车从图书馆出发,回家取相关证件并停留片刻后按原速度原路返回.两人距图书馆的路程 (米)与妈妈出发的时间 (分钟)之间的函数关系如图所示.
(1)、在图①中求作一点 ,使 ,且 、 在直线 异侧;(2)、在图②中求作一点 ,使 ,且 、 在直线 同侧.21. 小明写完作业后到图书馆找妈妈一起看书.小明从家出发,走了一段路程后突然发现钥匙与图书证忘带,立即打电话给妈妈(打电话时间忽略不计).妈妈立即骑车从图书馆出发,回家取相关证件并停留片刻后按原速度原路返回.两人距图书馆的路程 (米)与妈妈出发的时间 (分钟)之间的函数关系如图所示.(注:小明和妈妈始终沿同一条直道行进)
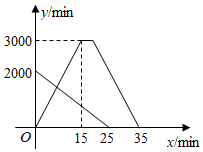 (1)、小明的速度是米/分,妈妈在家停留了分钟.(2)、当 为何值时,两人相距 .22. 如图①, 、 是两座垂直于同一水平地面且高度不同的铁塔.小明和小丽为了测量两座铁塔的高度,从地面上的点 处测得铁塔顶端 的仰角为39°,铁塔顶端 的仰角为27°,沿着 向前走20米到达点 处,测得铁塔顶端 的仰角为53°.已知 ,点 、 、 构成的 中, .
(1)、小明的速度是米/分,妈妈在家停留了分钟.(2)、当 为何值时,两人相距 .22. 如图①, 、 是两座垂直于同一水平地面且高度不同的铁塔.小明和小丽为了测量两座铁塔的高度,从地面上的点 处测得铁塔顶端 的仰角为39°,铁塔顶端 的仰角为27°,沿着 向前走20米到达点 处,测得铁塔顶端 的仰角为53°.已知 ,点 、 、 构成的 中, .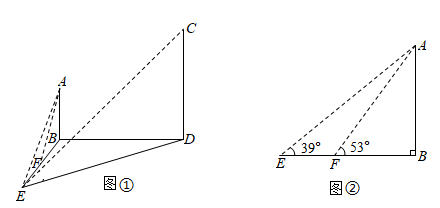
(参考数据: , , , , , , , , )
(1)、图②是图①中的一部分,求铁塔 的高度;(2)、小明说,在点 处只要再测量一个角,通过计算即可求出铁塔 的高度,那么可以测量的角是 , 若将这个角记为 ,则铁塔 的高度是;(用含 的式子表示)(3)、小丽说,除了在点 处测量角的度数外,还可以在点 处再测量一条线段的长度,通过计算也可求出铁塔 的高度,那么可以测量的线段是.(请写出两个不同的答案,可用文字描述)23. 已知关于 的一元二次方程 ( 为常数).(1)、若它的一个实数根是方程 的根,则 , 方程的另一个根为;(2)、若它的一个实数根是关于 的方程 的根,求 的值;(3)、若它的一个实数根是关于 的方程 的根,求 的最小值.24. 已知二次函数 ( 为常数,且 ).(1)、求二次函数的顶点坐标;(2)、设该二次函数图象上两点 、 ,点 和点 间(含点 、 )的图象上有一点 ,将点 纵坐标的最大值和最小值的差记为 .①当 时,若点 和点 关于二次函数对称轴对称,求 的值;
②若存在点 和点 使得 的值是4,则 的取值范围是 ▲ .
25. 如图①, 是 外一点, 与 相切于点 , 的延长线交 于点 ,过点 作 ,交 于点 ,连接 ,并延长 交 于点 ,连接 .已知 , 的半径为3.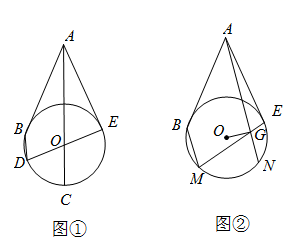 (1)、求证: 是 的切线;(2)、求 的长;(3)、如图②,若点 是 上一点,且 ,过 作 ,交弧 于点 ,连接 ,交 于点 ,连接 ,则 的长度是.26. 学完“探索三角形相似的条件”之后,小明所在的学习小组尝试探索四边形相似的条件,以下是他们的思考,请你和他们一起完成探究过程.
(1)、求证: 是 的切线;(2)、求 的长;(3)、如图②,若点 是 上一点,且 ,过 作 ,交弧 于点 ,连接 ,交 于点 ,连接 ,则 的长度是.26. 学完“探索三角形相似的条件”之后,小明所在的学习小组尝试探索四边形相似的条件,以下是他们的思考,请你和他们一起完成探究过程.(定义)四边成比例,且四角分别相等的两个四边形叫做相似四边形.
(1)、(初步思考)小明根据探索三角形相似的条件所获得的经验,考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”,“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件,于是,可以从“四边成比例,且一角对应相等的两个四边形相似”,“三边成比例,且两角分别相等的两个四边形相似”,“两边成比例,且三角分别相等的两个四边形相似”来探究.
(2)、(深入探究)学习小组一致认为,“四边成比例,且一角对应相等的两个四边形相似”是真命题,请结合图形完成证明.
已知:四边形 和四边形 中, , .
求证:四边形 四边形 .证明:
 (3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:
(3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:①“三边成比例,两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”;
②“三边成比例,两邻角分别相等且都不是其中两边的夹角的两个四边形相似”;
③“三边成比例及其两夹角分别相等的两个四边形相似”;
④“三边成比例,两对角分别相等的两个四边形相似”.
其中真命题是.(填写所有真命题的序号)
(4)、请你完成“两边成比例,且三角分别相等的两个四边形相似”的探究过程.