江苏省常州市武进区2021年数学中考一模试卷
试卷更新日期:2021-09-18 类型:中考模拟
一、单选题
-
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 若二次根式 有意义,则实数 的取值范围是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体中,其俯视图与主视图完全相同的是( )A、
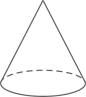 B、
B、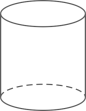 C、
C、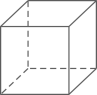 D、
D、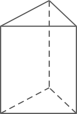 5. 如图,数轴上点 、 对应的数分别为 、 ,则下列不等式正确的是( )
5. 如图,数轴上点 、 对应的数分别为 、 ,则下列不等式正确的是( )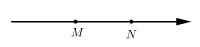 A、 B、 C、 D、6. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=44°时, 的大小为( )
A、 B、 C、 D、6. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=44°时, 的大小为( )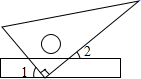 A、 B、 C、 D、7. 如图,等边 中, ,点 是 边上一点,则 的最小值是( )
A、 B、 C、 D、7. 如图,等边 中, ,点 是 边上一点,则 的最小值是( )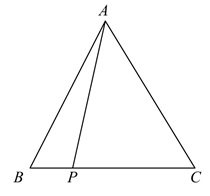 A、3 B、4 C、5 D、8. 如图,点 从菱形 的顶点 出发,沿 以 的速度匀速运动到点 .右图是点 运动时, 的面积 ( )随时间 ( )变化的关系图象,则 的值为( )
A、3 B、4 C、5 D、8. 如图,点 从菱形 的顶点 出发,沿 以 的速度匀速运动到点 .右图是点 运动时, 的面积 ( )随时间 ( )变化的关系图象,则 的值为( )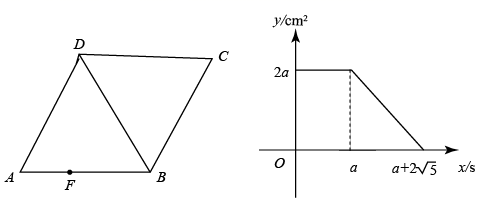 A、 B、3 C、 D、5
A、 B、3 C、 D、5二、填空题
-
9. 计算: .10. 如果 ,那么 的余角等于.11. 已知点 ,则点 到原点的距离是.12. 分解因式: .13. 截至2021年2月3日,由中国空间技术研究院研制的“天问一号”探测器飞行里程已超过450000000里,将数据450000000学记数法表示为.14. 若 是关于 的方程 的一个解,则 的值为.15. 二次函数 的图象与 轴有两个公共点,则 的取值范围是.16. 如图, 是 的内接三角形, , ,则 .
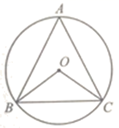 17. 如图,菱形 中, ,点 是 的中点,连接 ,则 .
17. 如图,菱形 中, ,点 是 的中点,连接 ,则 .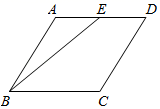 18. 如图,在平面直角坐标系 中,四边形 是矩形,其中点 、 分别在 轴、 轴上, . 是 轴负半轴上一点, ,过点 的直线分别与 轴、边 交于点 、点 ,连接 .当 与 相似时,则 的长为.
18. 如图,在平面直角坐标系 中,四边形 是矩形,其中点 、 分别在 轴、 轴上, . 是 轴负半轴上一点, ,过点 的直线分别与 轴、边 交于点 、点 ,连接 .当 与 相似时,则 的长为.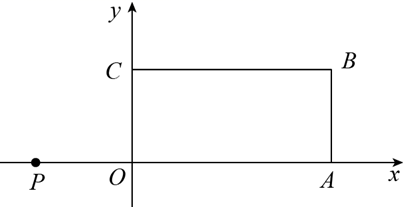
三、解答题
-
19. 先化简,再求值: ,其中 .20. 解方程和不等式:(1)、(2)、解不等式组:21. 小明为了了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必须且只能选择一门课程将获得的数据整理制如下两幅不完整的统计图.
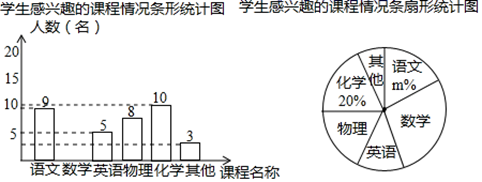
据统计图提供的信息,解答下列问题:
(1)、在这次调查中一共抽取了名学生, 的值是.(2)、请根据以上信息补全条形统计图;(3)、若该校九年级共有1500名学生,根据抽样调查的结果,请你估计该校九年级学生中对数学感兴趣的学生人数.22. 如图,将等边三角形、圆、平行四边形这三种图形分别画在3张大小、质地均相同的正方形小纸板上,将这3张正方形小纸板放入一只不透明的袋子中.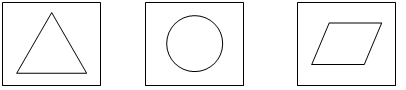 (1)、搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是.(2)、搅匀后从中模出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.23. 如图, 中, ,点 、 是 边上不重合的两点, .
(1)、搅匀后从中摸出一张小纸板,摸出的纸板上的图形是中心对称图形的概率是.(2)、搅匀后从中模出一张小纸板,记下纸板上图形的名称后放回袋子中,再从中摸出张小纸板,求两次摸出的小纸板上的图形都是轴对称图形的概率.23. 如图, 中, ,点 、 是 边上不重合的两点, .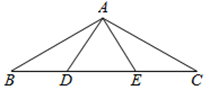 (1)、求证: ;(2)、若 , ,求 的大小.24. 某学校计划购买羽毛球拍和乒乓球拍,如果购买1副羽毛球拍与1副乒乓球拍,那么总费用为160元.如果购买3副羽毛球拍与2副乒乓球拍,那么总费用为420元.(1)、求购买1副羽毛球拍、1副乒乓球拍的费用分别是多少元?(2)、若该学校计划购买此类羽毛球拍和乒球拍共50副,并且总价格不超过3800元.最多能购买多少副羽毛球拍?25. 如图,在平面直角坐标系 中,过点 作 轴垂线交反比例函数 ( )图象于点 .在 延长线上取点 ,连接 ,交反比例函数 ( )图象于点 ,连接 , .
(1)、求证: ;(2)、若 , ,求 的大小.24. 某学校计划购买羽毛球拍和乒乓球拍,如果购买1副羽毛球拍与1副乒乓球拍,那么总费用为160元.如果购买3副羽毛球拍与2副乒乓球拍,那么总费用为420元.(1)、求购买1副羽毛球拍、1副乒乓球拍的费用分别是多少元?(2)、若该学校计划购买此类羽毛球拍和乒球拍共50副,并且总价格不超过3800元.最多能购买多少副羽毛球拍?25. 如图,在平面直角坐标系 中,过点 作 轴垂线交反比例函数 ( )图象于点 .在 延长线上取点 ,连接 ,交反比例函数 ( )图象于点 ,连接 , .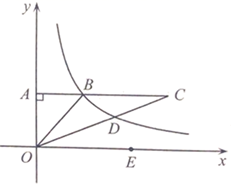 (1)、求 的值;(2)、在 轴正半轴上取点 ,当 平分 时,求点 的坐标.26. 中, , , ,点 是 边上的动点,连接 .
(1)、求 的值;(2)、在 轴正半轴上取点 ,当 平分 时,求点 的坐标.26. 中, , , ,点 是 边上的动点,连接 .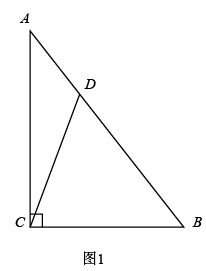
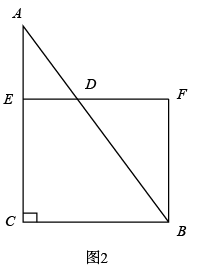
 (1)、如图1,当 是以 为腰的等腰三角形时, 长为;(2)、如图2,作 于点 ,作 交 于点 ,且 ,求 的长;(3)、将 沿 翻折得 ,若 ,求 的值.27. 在平面直角坐标系 中, 的半径为 , , 为 外两点, .给出如下定义:平移线段 ,使平移后的线段 成为 的弦(点 , 分别为点 , 的对应点),线段 长度的最小值称为线段 到 的“优距离”.
(1)、如图1,当 是以 为腰的等腰三角形时, 长为;(2)、如图2,作 于点 ,作 交 于点 ,且 ,求 的长;(3)、将 沿 翻折得 ,若 ,求 的值.27. 在平面直角坐标系 中, 的半径为 , , 为 外两点, .给出如下定义:平移线段 ,使平移后的线段 成为 的弦(点 , 分别为点 , 的对应点),线段 长度的最小值称为线段 到 的“优距离”.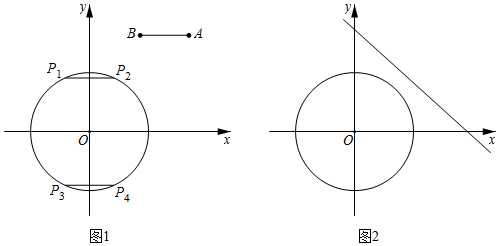 (1)、如图1, 中的弦 、 是由线段 平移而得,这两条弦的位置关系是;在点 , , , 中,连接点 与点的线段的长度等于线段 到 的“优距离”;(2)、若点 , ,线段 的长度是线段 到 的“优距离”,则点 的坐标为;(3)、如图2,若 , 是直线 上两个动点,记线段 到 的“优距离”为 ,则 的最小值是;请你在图2中画出 取得最小值时的示意图,并标记相应的字母.28. 如图,平面直角坐标系 中,抛物线 与 轴交于 , ,与 轴交于点 .
(1)、如图1, 中的弦 、 是由线段 平移而得,这两条弦的位置关系是;在点 , , , 中,连接点 与点的线段的长度等于线段 到 的“优距离”;(2)、若点 , ,线段 的长度是线段 到 的“优距离”,则点 的坐标为;(3)、如图2,若 , 是直线 上两个动点,记线段 到 的“优距离”为 ,则 的最小值是;请你在图2中画出 取得最小值时的示意图,并标记相应的字母.28. 如图,平面直角坐标系 中,抛物线 与 轴交于 , ,与 轴交于点 .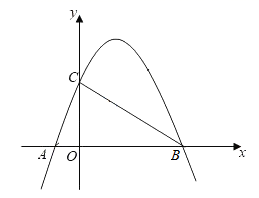 (1)、 ; ;(2)、若直线 经过点 ,点 关于直线 的对称点 恰好在线段 上,直线 与抛物线交于另一点 ;
(1)、 ; ;(2)、若直线 经过点 ,点 关于直线 的对称点 恰好在线段 上,直线 与抛物线交于另一点 ;①求点 的坐标;
②点 是直线 上一点,若对于在第一象限内的抛物线 上的动点 始终有 ,请直接写出 的取值范围.