陕西省西安市三校2020-2021学年高一上学期理数联考试卷

试卷更新日期：2021-09-18 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {1, 2, 3, 4}, B = {x | x = n^{2}, n \in A}$ ，则 $A \cap B =$ （）

A、 ${1, 4}$ B、 ${2, 3}$ C、 ${9, 16}$ D、 ${1, 2}$

查看试题解析
2. 已知幂函数 $f (x)$ 的图象过点 $(4 ， \frac{1}{2})$ ，则 $f (9)$ 的值为（）

A、 $\frac{1}{3}$ B、3 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
3. 曲线y=x²+3x在点A(1，4)处的切线的斜率k是（）

A、4 B、5 C、6 D、7

查看试题解析
4. 下列函数中为偶函数的是（）

A、 $y = x^{2} \sin x$ B、 $y = x^{2} \cos x$ C、 $y = | \ln x |$ D、 $y = 2^{- x}$

查看试题解析
5. 函数 $f (x) = \ln \frac{3 x}{2} - \frac{2}{x}$ 的零点一定位于区间（）

A、 $(1 ， 2)$ B、 $(2 ， 3)$ C、 $(3 ， 4)$ D、 $(4 ， 5)$

查看试题解析
6. 已知函数 $f (x) = \lg \frac{e^{x} - e^{- x}}{2}$ ，则f(x)是（）

A、非奇非偶函数，且在(0，+∞)上单调递增 B、奇函数，且在R上单调递增 C、非奇非偶函数，且在(0，+∞)上单调递减 D、偶函数，且在R上单调递减

查看试题解析
7. 设 $f (x)$ 是定义域为 $R$ 的偶函数，且在 $(0 ， + \infty)$ 单调递减， $a = \log_{2} \frac{1}{3}$ ， $b = 3^{- 0.1}$ ， $c = 3^{- \frac{1}{2}}$ 则（）

A、 $f (a) > f (b) > f (c)$ B、 $f (a) > f (c) > f (b)$ C、 $f (c) > f (a) > f (b)$ D、 $f (c) > f (b) > f (a)$

查看试题解析
8. 已知函数 $f (x) = {\begin{matrix} (2 - a) x + 3 a ， x < 1 \\ \log_{3} x ， \begin{matrix} \end{matrix} x \geq 1 \end{matrix}$ 的值域为R，则实数a的取值范围是（）

A、(-1，2) B、 $[- 1 ， 2)$ C、 $(- \infty ， - 1]$ D、{-1}

查看试题解析
9. 已知 $f (x)$ 是定义域为 $(- \infty ， + \infty)$ 的奇函数，满足 $f (1 - x) = f (1 + x)$ .若 $f (1) = 2$ ，则 $f (1) + f (2) + f (3) + \dots + f (2022)$ =（）

A、 $- 50$ B、0 C、50 D、2

查看试题解析
10. 如图，在直角梯形ABCD中，AB⊥BC，AD＝DC＝2，CB＝ $\sqrt{2}$ ，动点P从点A出发，由A→D→C→B沿边运动，点P在AB上的射影为Q.设点P运动的路程为x，△APQ的面积为y，则y＝f(x)的图象大致是（）

A、 B、 C、 D、

查看试题解析
11. 若函数 $f (x) = \frac{1}{3} x^{3} - \frac{3}{2} x^{2} + a x + 4$ 在区间(0，4)上不单调，则实数a的取值范围为（）

A、 $[- 4 ， \frac{9}{4})$ B、 $[0 ， \frac{9}{4}]$ C、 $(- 4 ， \frac{9}{4})$ D、 $(0 ， \frac{9}{4})$

查看试题解析
12. 设定义域为 $R$ 的函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，且满足 $f^{'} (x) > f (x)$ ，则不等式 $e^{x + 1} f (x) > f (2 x + 1)$ 的解集为（）

A、 $(- 1 ， + \infty)$ B、 $(- \infty ， - 1)$ C、 $(- \frac{1}{2} ， + \infty)$ D、 $(- \infty ， 1)$

查看试题解析

二、填空题

13. 函数 $f (x) = x^{\frac{1}{2}} - {(\frac{1}{2})}^{x}$ 的零点个数为.

查看试题解析
14. 已知函数 $f (x)$ 满足 $f (x + 4) = f (x) (x \in R)$ ，且在区间(-2，2]上， $f (x) = {\begin{matrix} | x + 1 | ， - 2 < x \leq 0 \\ \cos \frac{π x}{2} ， 0 < x \leq 2 \end{matrix}$ ，则 $f (f (2021))$ 的值为.

查看试题解析
15. 函数 $y = x^{2} - 2 x + 3$ 在定义域 $[m ， 4]$ 上的值域为 $[2 ， 11]$ ，则实数m的取值范围是.

查看试题解析
16. 函数 $f (x)$ 的定义域为A，若 $x_{1} ， x_{2} \in A$ 且 $f (x_{1}) = f (x_{2})$ 时总有 $x_{1} = x_{2}$ ，则称 $f (x)$ 为单函数.例如：函数 $f (x) = 3 x - 2 (x \in R)$ 是单函数.给出下列命题：
①函数 $f (x) = 2 x^{2} + 1 (x \in R)$ 是单函数；

②对数函数 $f (x) = \ln x$ 是单函数；

③若 $f (x)$ 为单函数， $x_{1} ， x_{2} \in A$ 且 $x_{1} \neq x_{2}$ ，则 $f (x_{1}) \neq f (x_{2})$ ；

④在定义域上具有单调性的函数一定是单函数，

其中的真命题是.(写出所有真命题的序号)

查看试题解析

三、解答题

17. 设命题p：实数x满足 $x^{2} - 4 a x + 3 a^{2} < 0$ ，其中 $a > 0$ ；命题q：实数x满足 $\frac{x - 3}{x - 2} \leq 0$

(1)、若 $a = 1$ 且p $\land$ q为真，求实数 $x$ 的取值范围；

(2)、若 $\neg p$ 是 $\neg q$ 的充分不必要条件，求实数 $a$ 的取值范围.

查看试题解析
18. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，且当 $x < 0$ 时， $f (x) = - 2^{- x} + 3 \cdot 2^{x}$ .

(1)、当 $x > 0$ 时，求 $f (x)$ 的解析式；

(2)、若 $f (x) = \frac{1}{2}$ ，求 $x$ 的值.

查看试题解析
19. 已知函数g(x)=ax²-2ax+1+b(a>0)在区间 $[2, 4]$ 上有最大值9和最小值1，设函数 $f (x) = \frac{g (x)}{x}$ .

(1)、求a､b的值；

(2)、若不等式f(2^x)-k·2^x≥0在x∈[-1，1]上恒成立，求实数k的取值范围.

查看试题解析
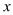20. 商场销售某种商品的经验表明，该商品每日的销售量 (单位：千克)与销售价格 (单位：元/千克)满足关系式 $y = \frac{a}{x - 3} + 10 {(x - 6)}^{2}$ ，其中3<x<6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．

(1)、求a的值；

(2)、若商品的成品为3元/千克，试确定销售价格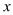的值，使商场每日销售该商品所获得的利润最大

查看试题解析
21. 设函数 $f (x) = - \frac{a \ln x}{x} + x - a + 2 (a \in R)$ .

(1)、当曲线 $y = f (x)$ 在点(1，f (1))处的切线与直线y=x垂直时，求a的值；

(2)、若函数 $F (x) = f (x) + \frac{a^{2}}{4 x}$ 有两个零点，求实数a的取值范围.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，曲线 $C$ 的参数方程为 ${\begin{array}{l} x = 3 \cos α \\ y = \sin α \end{array}$ （ $α$ 为参数），在以原点为极点， $x$ 轴正半轴为极轴的极坐标系中，直线 $l$ 的极坐标方程为 $ρ \sin (θ - \frac{π}{4}) = \sqrt{2}$ .

(1)、求曲线 $C$ 和直线 $l$ 的普通方程；

(2)、设点 $P (0 ， 2)$ ， $l$ 和 $C$ 交于 $A$ 、 $B$ 两点，求 $| P A | + | P B |$ .

查看试题解析
23. 已知函数 $f (x) = | x + 1 |$ .

(1)、求不等式 $f (x) < | 2 x + 1 | - 1$ 的解集 $M$ ；

(2)、设 $a, b \in M$ ，证明： $f (a b) > f (a) - f (- b)$ .

查看试题解析