湖南省岳阳市城区二十八校2021年数学中考一模联考试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 电梯上升16层记为+16,下降5层记为( )A、+5 B、 C、 D、-52. 下列因式分解正确的是( )A、 B、 C、 D、3.
图中是一个少数民族手鼓的轮廓图,其主视图是( )
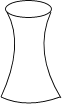 A、
A、 B、
B、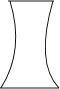 C、
C、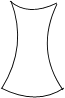 D、
D、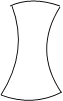 4. 岳阳是国家历史文化名城,区域内的岳阳楼、君山岛、张谷英村、屈子祠、左宗棠故居都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学旅行,人数分别为:13,8,12,9,8(单位:人),这组数据的众数和中位数分别是( )A、9人,8人 B、8人,12人 C、8人,9人 D、9人,12人5. 不等式组 的解集在数轴上表示为( )A、
4. 岳阳是国家历史文化名城,区域内的岳阳楼、君山岛、张谷英村、屈子祠、左宗棠故居都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学旅行,人数分别为:13,8,12,9,8(单位:人),这组数据的众数和中位数分别是( )A、9人,8人 B、8人,12人 C、8人,9人 D、9人,12人5. 不等式组 的解集在数轴上表示为( )A、 B、
B、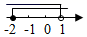 C、
C、 D、
D、 6. 如图,在 中, ,以顶点B为圆心,适当长度为半径画弧,分别交 ,BC于点M,N,再分别以点M,N为圆心,以大于 的长为半径作弧,两弧相交于点P;作射线BP交AC于点D,若CD=4,则点D到 的距离为( )
6. 如图,在 中, ,以顶点B为圆心,适当长度为半径画弧,分别交 ,BC于点M,N,再分别以点M,N为圆心,以大于 的长为半径作弧,两弧相交于点P;作射线BP交AC于点D,若CD=4,则点D到 的距离为( )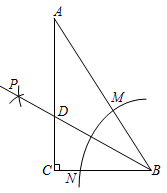 A、4 B、3 C、 D、17. 下列命题是真命题的是( )A、同弧所对的圆心角相等 B、对角线互相垂直的四边形是菱形 C、二次函数 的图象与坐标轴有两个交点 D、若 ,则8. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
A、4 B、3 C、 D、17. 下列命题是真命题的是( )A、同弧所对的圆心角相等 B、对角线互相垂直的四边形是菱形 C、二次函数 的图象与坐标轴有两个交点 D、若 ,则8. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 ,则 (n为正整数)的坐标是( )
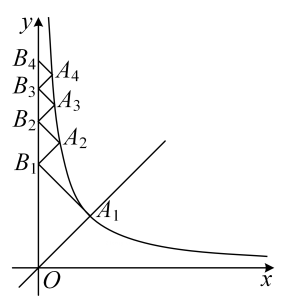 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
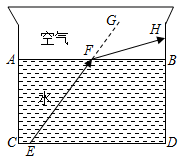
9. 岳阳“马赛克”建筑广电中心,耗资176000000元,数据176000000用科学记数法表示为.10. 若 与 的和为单项式,则 .11. 函数y= 中,自变量x的取值范围是.12. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面 与水杯下沿 平行,光线变成 ,点G在射线 上, ,则 °.
 13. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是.14. 如图,点O是矩形纸片 的对称中心,点E在 上,将纸片沿AE折叠后,点B与点O重合,若 ,则矩形ABCD的周长为.
13. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是.14. 如图,点O是矩形纸片 的对称中心,点E在 上,将纸片沿AE折叠后,点B与点O重合,若 ,则矩形ABCD的周长为.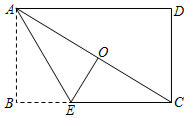 15. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?设合伙人数为x人,羊价为y元.16. 如图, 内接于⊙O, 平分 交 边于点E,过点D作⊙O的切线,过点A作 于点F,设 ,⊙O的半径为R, 则下列结论正确的是.(写出所有正确结论的序号)
15. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?设合伙人数为x人,羊价为y元.16. 如图, 内接于⊙O, 平分 交 边于点E,过点D作⊙O的切线,过点A作 于点F,设 ,⊙O的半径为R, 则下列结论正确的是.(写出所有正确结论的序号)① ;② ;③ ;④ .

三、解答题
-
17.(1)、计算: .(2)、先化简: ,再从 中选取一个合适的整数,代入求值.18. 如图,E、F、G、H为四边形 各边的中点,对角线 .求证:四边形 为菱形.
 19. 如图,已知直线 与双曲线 交于 , 两点(A与B不重合),直线 与x轴交于点 ,与y轴交于点C.
19. 如图,已知直线 与双曲线 交于 , 两点(A与B不重合),直线 与x轴交于点 ,与y轴交于点C. (1)、若A,B两点的坐标分别为 , ,求两函数的解析式;(2)、在(1)的条件下,求证: ;(3)、猜想并用等式表示 , , 之间的关系(不要求证明).20. 某校数学实践小组就近期人们比较关注的五个话题:A.5G通讯:B.民法典;C.北斗导航;D.数字经济; .小康社会,对某小区居民进行了随机抽样调查,每人只能从中选择一个本人最关注的话题
(1)、若A,B两点的坐标分别为 , ,求两函数的解析式;(2)、在(1)的条件下,求证: ;(3)、猜想并用等式表示 , , 之间的关系(不要求证明).20. 某校数学实践小组就近期人们比较关注的五个话题:A.5G通讯:B.民法典;C.北斗导航;D.数字经济; .小康社会,对某小区居民进行了随机抽样调查,每人只能从中选择一个本人最关注的话题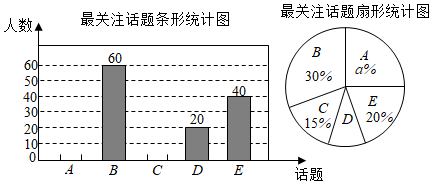
请结合图中的信息解决下列问题:
(1)、在这次活动中,调查的居民共有人;(2)、将条形统计图补充完整;(3)、扇形统计图中的a= , D所在扇形的圆心角是度;(4)、该小组讨论中,甲、乙两个小组从三个话题:A.5G通讯;B.民法典;C.北斗导航(不放回)选一项进行发言,利用树状图或表格求出两个小组选择A、B话题发言的概率?21. 随着某市养老机构建设的稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从2018年底的2万个增长到2020年底的2.88万个,求该市这两年(从2018年度到2020年底)拥有的养老床位数的平均年增长率;(2)、若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间t个(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要( ),且双人间的房间数是单人间的2倍.设该养老中心建成后能提供养老床位y个,求y与t的函数关系式22. 某体育看台侧面的示意图如图所示,观众区 的坡度i为1:2,顶端C离水平地面 的高度为 ,竖直的立杆上C、D两点间的距离为 ,E处到观众区底端A处的水平距离 为 .求: (1)、观众区的水平宽度 ;(2)、顶棚的E处离地面的高度 .( , ,结果精确到 )23. 一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现 且 .
(1)、观众区的水平宽度 ;(2)、顶棚的E处离地面的高度 .( , ,结果精确到 )23. 一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现 且 .小组讨论后,提出了下列三个问题,请你帮助解答:
 (1)、将正方形 绕点A按逆时针方向旋转(如图1),还能得到 吗?若能,请给出证明,请说明理由;(2)、把背景中的正方形分别改成菱形 和菱形 ,将菱形 绕点A按顺时针方向旋转(如图2),试问当 与 的大小满足怎样的关系时, ;(3)、把背景中的正方形分别改写成矩形 和矩形 ,且 , , (如图3),连接 , .试求 的值(用a,b表示).24. 如图,抛物线 过点 ,A .点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接 .
(1)、将正方形 绕点A按逆时针方向旋转(如图1),还能得到 吗?若能,请给出证明,请说明理由;(2)、把背景中的正方形分别改成菱形 和菱形 ,将菱形 绕点A按顺时针方向旋转(如图2),试问当 与 的大小满足怎样的关系时, ;(3)、把背景中的正方形分别改写成矩形 和矩形 ,且 , , (如图3),连接 , .试求 的值(用a,b表示).24. 如图,抛物线 过点 ,A .点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接 . (1)、求抛物线的解析式;(2)、如图①,当 时,求点D的坐标;(3)、如图②,在(2)的条件下,抛物线的对称轴交x轴于点C,交OD于点E,点F是线段 上的动点(点F不与点O和点B重合),连接 ,点B关于直线EF的对应点为点 , 与 的重叠部分为 ,使以点E,F,G,H为顶点的四边形是矩形?若存在,求出点H的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图①,当 时,求点D的坐标;(3)、如图②,在(2)的条件下,抛物线的对称轴交x轴于点C,交OD于点E,点F是线段 上的动点(点F不与点O和点B重合),连接 ,点B关于直线EF的对应点为点 , 与 的重叠部分为 ,使以点E,F,G,H为顶点的四边形是矩形?若存在,求出点H的坐标;若不存在,请说明理由.