湖南省岳阳市城区二十八校2021年数学中考二模联考试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 在实数0.1, ,0,-3中,最小的数是( )A、-3 B、 C、0 D、0.12. 下列医护图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 式子 在实数范围内有意义,则x的取值范围是( )A、x≥0 B、x≥﹣1 C、x≥1 D、x≤﹣14. 下列运算正确的是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、平行四边形的对角线相等 B、相似三角形对应周长的比等于相似比的平方 C、圆内接四边形的对角互补 D、三角形的内心是三边的垂直平分线的交点6. 对于一组统计数据3,3,6,5,8,下列说法错误的是( )A、众数是3 B、平均数是5 C、中位数是5 D、方差是1.67. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( )
3. 式子 在实数范围内有意义,则x的取值范围是( )A、x≥0 B、x≥﹣1 C、x≥1 D、x≤﹣14. 下列运算正确的是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、平行四边形的对角线相等 B、相似三角形对应周长的比等于相似比的平方 C、圆内接四边形的对角互补 D、三角形的内心是三边的垂直平分线的交点6. 对于一组统计数据3,3,6,5,8,下列说法错误的是( )A、众数是3 B、平均数是5 C、中位数是5 D、方差是1.67. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( ) A、37° B、43° C、53° D、54°8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、
A、37° B、43° C、53° D、54°8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、 B、
B、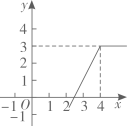 C、
C、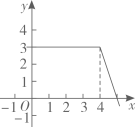 D、
D、
二、填空题
-
9. 一个六边形的内角和是.10. 因式分解: = .11. 来自国务院联防联控机制的最新消息显示,截至2021年3月22日24时,我国接种新冠疫苗8050万剂次,接种人数稳步增长.那么数据8050万用科学记数法可以表示为.12. 计算: =.13. 方程(x+1)2=4的解是.14. 数学文化我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五丈,中斜十二丈,大斜十三丈,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5丈,12丈,13丈,问这块沙田面积有多大?(题中的“丈”是我国市制长度单位,1丈=10尺.)则该沙田的面积为平方丈.15. 如图,在长方形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是
 16. 如图,已知点C是以 为直径的⊙O上一点, 于点H,过点B作⊙O的切线交直线 于点D,点E为 的中点,连接 并延长交 于点F,连接 .给出下列结论:① ;② 是⊙O的切线;③若 ,则⊙O的半径为 ;④若 ,⊙O的半径为3,则弧 的长 .其中正确的有(写出所有正确结论的序号)
16. 如图,已知点C是以 为直径的⊙O上一点, 于点H,过点B作⊙O的切线交直线 于点D,点E为 的中点,连接 并延长交 于点F,连接 .给出下列结论:① ;② 是⊙O的切线;③若 ,则⊙O的半径为 ;④若 ,⊙O的半径为3,则弧 的长 .其中正确的有(写出所有正确结论的序号)
三、解答题
-
17. 计算:18. 如图,在 ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
 19. 如图,直线 与双曲线 相交于 、 两点,与y轴相交于点C.
19. 如图,直线 与双曲线 相交于 、 两点,与y轴相交于点C.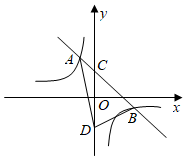 (1)、求直线 与双曲线的解析式;(2)、若点D与点C关于x轴对称,求 的面积.20. 岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.(1)、求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?(2)、学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?21. 随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
(1)、求直线 与双曲线的解析式;(2)、若点D与点C关于x轴对称,求 的面积.20. 岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.(1)、求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?(2)、学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?21. 随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.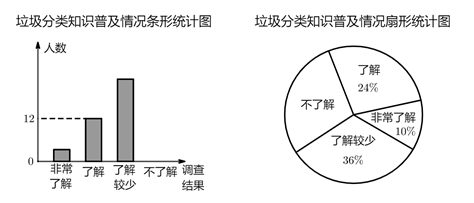 (1)、本次被调查的学生有多少名?补全条形统计图.(2)、估计该校4000名学生中“非常了解”与“了解”的人数和是多少.(3)、被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 如图是某户外看台的截面图,长 的看台 与水平地面 的夹角为35°,与 平行的平台 长为 ,点F是遮阳棚 上端E正下方在地面上的一点,测得 ,在挡风墙 的点D处测得点E的仰角为26°,求遮阳棚 的长(计算结果精确到十分位).
(1)、本次被调查的学生有多少名?补全条形统计图.(2)、估计该校4000名学生中“非常了解”与“了解”的人数和是多少.(3)、被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 如图是某户外看台的截面图,长 的看台 与水平地面 的夹角为35°,与 平行的平台 长为 ,点F是遮阳棚 上端E正下方在地面上的一点,测得 ,在挡风墙 的点D处测得点E的仰角为26°,求遮阳棚 的长(计算结果精确到十分位).(参考数据: , , ,)
 23. 已知四边形 中, 、 分别是 、 边上的点, 与 交于点 .
23. 已知四边形 中, 、 分别是 、 边上的点, 与 交于点 . (1)、如图1,若四边形 是矩形,且 ,求证: ;(2)、如图2,若四边形 是平行四边形,试探究:当 与 满足什么关系时,使得 成立?并证明你的结论;(3)、如图3,若 , , , ,请直接写出 的值.24. 在平面直角坐标系 中,已知抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)、如图1,若四边形 是矩形,且 ,求证: ;(2)、如图2,若四边形 是平行四边形,试探究:当 与 满足什么关系时,使得 成立?并证明你的结论;(3)、如图3,若 , , , ,请直接写出 的值.24. 在平面直角坐标系 中,已知抛物线 与 轴交于 , 两点,与 轴交于点 .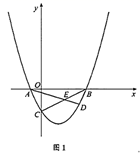
 (1)、求抛物线的函数表达式(2)、如图1,点 为第四象限抛物线上一点,连接 , 交于点 ,连接 ,记 的面积为 , 的面积为 ,求 的最大值;(3)、如图2,连接 , ,过点 作直线 ,点 , 分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点 , ,使 .若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式(2)、如图1,点 为第四象限抛物线上一点,连接 , 交于点 ,连接 ,记 的面积为 , 的面积为 ,求 的最大值;(3)、如图2,连接 , ,过点 作直线 ,点 , 分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点 , ,使 .若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.