湖南省娄底市娄星区2021年数学中考模拟试卷

试卷更新日期：2021-09-16 类型：中考模拟

进入出卷网下载

一、单选题

1. -2021的倒数是（）

A、2021 B、 $\frac{1}{2021}$ C、-2021 D、 $- \frac{1}{2021}$

查看试题解析
2. 下列运算正确的是（）

A、 ${(a - b)}^{2} = a^{2} - b^{2}$ B、 $2 a + b = 2 a b$ C、 ${(a^{3})}^{2} = a^{6}$ D、 ${(- 2 a)}^{2} = - 4 a^{4}$

查看试题解析
3. 下列结论中，不一定成立的是（）

A、平行四边形对边平行 B、平行四边形对角相等 C、平行四边形对角线互相平分 D、平行四边形对角线相等

查看试题解析
4. 某地一周七天的最高气温（单位： $℃$ ）分别如下：25，20，17，18，14，17，11，这组数据的中位数是（）

A、18 B、17 C、14 D、20

查看试题解析
5. 如图， $A B$ 平行 $C D ， E F$ 交 $A B$ 于点 $G ， E M$ 平分 $∠ C E F ， ∠ F G B = 70 °$ ，则 $∠ B M E$ 的度数为（）

A、 $70 °$ B、 $50 °$ C、 $65 °$ D、 $55 °$

查看试题解析
6. 如图， $B D$ 与 $C E$ 相交于点 $A ， D E$ 平行 $B C ， D E ： B C = 2 ： 3$ ，则 $△ A B C$ 与 $△ A D E$ 的面积之比为（）

A、2：3 B、3：2 C、4：9 D、9：4

查看试题解析
7. 国家统计局2021年1月18日发布数据，2020年我国国内生产总值 $(GDP)$ 首次突破100万亿元大关，达到101.6万亿元，其中101.6万亿元用科学记数法表示为（）

A、 $1.016 \times 10^{10}$ 元 B、 $1.016 \times 10^{12}$ 元 C、 $1.016 \times 10^{14}$ 元 D、 $1.016 \times 10^{16}$ 元

查看试题解析
8. 在下列图形中：等边三角形､平行四边形､等腰直角三角形､矩形，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、等腰直角三角形 D、矩形

查看试题解析
9. 方程 $x^{2} + 2 \sqrt{3} x - 3 = 0$ 根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、有一个实数根

查看试题解析
10. 入射光线和平面镜的夹角为 $40 °$ ，转动平面镜，使入射角减小 $10 °$ ，反射光线与入射光线的夹角和原来相比较将（）

A、减小 $40 °$ B、减小 $10 °$ C、减小 $20 °$ D、不变

查看试题解析
11. 如图，在 $⊙ O$ 中， $O A ､ O B$ 为半径， $A B ､ A C ､ B C$ 为弦，若 $∠ O A B = 70 °$ ，则 $∠ C$ 的度数为（）

A、 $40 °$ B、 $70 °$ C、 $20 °$ D、 $30 °$

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列结论：① $a b c > 0$ ；② $2 a - b > 0$ ；③ $4 a - 2 b + c < 0$ ；④ ${(a + c)}^{2} < b^{2}$ .其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

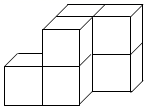
13. 从 $\sqrt{3}$ ， $π$ ，0，3.14， $\sqrt{4}$ ，0.2020020002…（两个2之间依次多一个0）这六个数中随机抽取一个，抽到有理数的概率是.

查看试题解析
14. 函数y＝ $\sqrt{1 - x}$ 中，自变量x的取值范围是．

查看试题解析
15. 将7个棱长为1的小立方体摆成如图所示几何体，该几何体的俯视图的面积为.

查看试题解析
16. 如图，点 $A ， C$ 均在双曲线 $y = \frac{4}{x}$ 上运动， $A B ⊥ x$ 轴， $A C = B C$ ，则 $△ A B C$ 的面积是.

查看试题解析
17. 材料：从 $A ､ B ､ C$ 三人中选取二人当代表，有 $A$ 和 $B ､ A$ 和 $C ､ B$ 和 $C$ 三种不同的选法，抽象成数学模型是：从3个元素中选取2个元素组合，记作 $C_{3}^{2} = \frac{3 \times 2}{2 \times 1} = 3$ .一般地，从 $m$ 个元素中选取 $n$ 个元素组合，记作 $C_{m}^{n} = \frac{m \times (m - 1) \times (m - 2) \times \dots \times (m - n + 1)}{n \times (n - 1) \times (n - 2) \times \dots \times 3 \times 2 \times 1}$ .
问题：从7个人中选取4个人当代表，不同的选法有种.

查看试题解析
18. 如图，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，摆第 $n$ 个图案需要枚棋子.

查看试题解析

三、解答题

19. 计算： $| \sqrt{2} - 1 | + {(3.14 - π)}^{0} - 2 \sin 45^{°} + {(\frac{1}{2021})}^{- 1}$ .

查看试题解析
20. 先化简 $(\frac{2}{x + 2} + \frac{4}{x^{2} - 4}) \div \frac{x}{x^{2} + 4 x + 4}$ ，然后从 $- 2$ ，0，1，2中选一个合适的数代入求值.

查看试题解析
21. 为了解中学生对我国传统节日习俗的知晓情况，某校数学兴趣小组在全校开展了随机调查，将调查结果进行量化，量化分数 $T$ 分成四个层次：A. $90 \leq T \leq 100$ ，B. $80 \leq T < 90$ ，C. $60 \leq T < 80$ ，D. $T < 60$ ，把所得数据绘制成了两个统计图，请根据图中信息解答下列问题：

(1)、本次一共随机调查了名学生，扇形统计图中 $C$ 所在扇形的圆心角是度.

(2)、计算 $D$ 层次 $(T < 60)$ 的学生人数并补全条形统计图.

(3)、若该校共有6000名学生，则对我国传统节日习俗知晓 $(T \geq 80)$ 的学生大约有多少人？

查看试题解析
22. 为积极响应党中央号召，推进乡村振兴，某地区对 $A ､ B$ 两地间的公路进行改建，如图， $A ､ B$ 两地间有一座山，汽车原来从 $A$ 地到 $B$ 地需要途径 $C$ 地沿折线 $A C B$ 行驶，现开通隧道后，汽车可直接沿直线 $A B$ 行驶，已知 $A C = 40$ 千米， $∠ A = 30 ° ， ∠ B = 45 °$ .

（结果精确到0.1千米，参考数据： $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ）.

(1)、开通隧道前，汽车从 $A$ 到 $B$ 地大约要走多少千米？

(2)、开通隧道后，汽车从 $A$ 到 $B$ 地大约可以少走多少千米？

查看试题解析
23. 2021年是中国共产党建党100周年，全国上下正在开展党史学习教育活动.为给党员提供学习资料，某单位计划花6000元购进《论中国共产党历史》和《中国共产党简史》共200本，其中《论中国共产党历史》的价格是26元/本，《中国共产党简史》的价格是42元/本.求：

(1)、该单位计划购进《论中国共产党历史》和《中国共产党简史》各多少本？

(2)、为节约开支，该单位决定只购进这两种书共100本，总费用不超过3500元.那么，该单位最少要购进《论中国共产党历史》多少本？

查看试题解析
24. 已知：如图所示，在 $△ A B C$ 中， $D$ 是 $A C$ 的中点， $E$ 是线段 $B C$ 的延长线上一点，过点 $A$ 作 $A F$ 平行 $B E$ ，交线段 $E D$ 的延长线于点 $F$ ，连接 $A E ､ C F$ .

(1)、求证： $A F = C E$ ；

(2)、若 $A F = C F = 4 ， ∠ A F D = 30 °$ ，求 $E F$ 的长.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 分别与 $B C ､ A C$ 交于点 $D ､ E$ ，过点 $D$ 作 $D F ⊥ A C$ ，垂足为点 $F$ .

(1)、求证：直线 $D F$ 是 $⊙ O$ 的切线；

(2)、求证： $B C^{2} = 4 C F \cdot A B$ ；

(3)、若 $⊙ O$ 的半径为2， $∠ C D F = 22.5 °$ ，求图中阴影部分的面积.

查看试题解析
26. 如图，抛物线 $y = a (x + 3) (x - 1)$ 与 $x$ 轴相交于 $A ､ B$ 两点（点 $A$ 在点 $B$ 右侧），过点 $A$ 的直线交抛物线于另一点 $C$ ，点 $C$ 的坐标为 $(- 2 ， 6)$ .

(1)、求 $a$ 的值及直线 $A C$ 的函数关系式；

(2)、 $P$ 是线段 $A C$ 上一动点，过点 $P$ 作 $y$ 轴的平行线，交抛物线于点 $M$ ，交 $x$ 轴于点 $N$ .
①求线段 $P M$ 长度的最大值；

②在抛物线上是否存在这样的点 $M$ ，使得 $△ C M P$ 与 $△ A P N$ 相似？如果存在，请求出满足条件的点 $M$ 的坐标；如果不存在，请说明理由.

查看试题解析