湖北省宜昌市西陵区2021年数学中考模拟试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 将如图所示的蜜蜂图案平移后可以得到下图中的( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 中国是严重缺水的国家之一,人均淡水资源为世界人均量的四分之一,所以我们倡导为中国节水,为世界节水,若每人每天浪费水0.32L,那么100万人每天浪费的水,用科学记数法表示为( )A、 B、 C、 D、3. 实数-2, ,-0.2, , , 中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个4. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )
2. 中国是严重缺水的国家之一,人均淡水资源为世界人均量的四分之一,所以我们倡导为中国节水,为世界节水,若每人每天浪费水0.32L,那么100万人每天浪费的水,用科学记数法表示为( )A、 B、 C、 D、3. 实数-2, ,-0.2, , , 中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个4. 如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )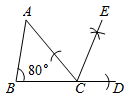 A、 B、 C、 D、5. 如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是( )A、同一行 B、同一列 C、同行同列 D、不同行不同列6. 可以用来说明命题“若 a2=b2 , 则 a=b ”是假命题的反例是( )A、 B、 C、 D、7. 从左面观察如图所示的几何体,看到的平面图形是( )
A、 B、 C、 D、5. 如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是( )A、同一行 B、同一列 C、同行同列 D、不同行不同列6. 可以用来说明命题“若 a2=b2 , 则 a=b ”是假命题的反例是( )A、 B、 C、 D、7. 从左面观察如图所示的几何体,看到的平面图形是( ) A、
A、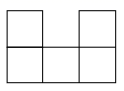 B、
B、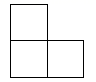 C、
C、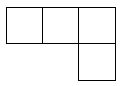 D、
D、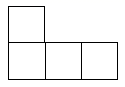 8. 丽华根据演讲比赛中九位评委所给的分数作了如下表格
8. 丽华根据演讲比赛中九位评委所给的分数作了如下表格平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、平均数 B、众数 C、方差 D、中位数9. 如图,在 中, , , , 是它的中线,以C为圆心, 为半径作 ,则点M与 的位置关系为( )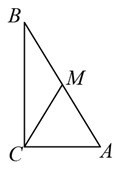 A、点M在 上 B、点M在 内 C、点M在 外 D、点M不在 内10. 已知,在△ABC中, ,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
A、点M在 上 B、点M在 内 C、点M在 外 D、点M不在 内10. 已知,在△ABC中, ,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( ) A、 B、△BCD是等边三角形 C、AD垂直平分BC D、11. 二次函数 的图象如图所示,则一次函数 和反比例函数 在同一平面直角坐标系中的图象可能是( )
A、 B、△BCD是等边三角形 C、AD垂直平分BC D、11. 二次函数 的图象如图所示,则一次函数 和反比例函数 在同一平面直角坐标系中的图象可能是( )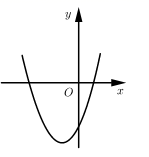 A、
A、 B、
B、 C、
C、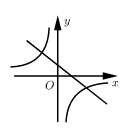 D、
D、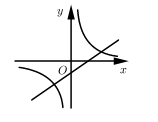
二、填空题
-
12. 某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减/辆
-1
+3
-2
+4
+7
-5
-10
生产量最多的一天比生产量最少的一天多生产辆.
13. 如图,一块飞镖游戏板由大小相等的小正方形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),击中黑色区域的概率是.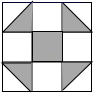 14. 四边形 在平面直角坐标系中的位置如图所示,已知点A(3,0),C(2,2),若要使四边形 为平行四边形,那么点B的坐标为.
14. 四边形 在平面直角坐标系中的位置如图所示,已知点A(3,0),C(2,2),若要使四边形 为平行四边形,那么点B的坐标为.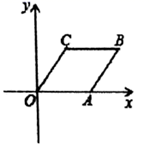 15. 通过你的观察并总结规律,第四个图形中y的值是.
15. 通过你的观察并总结规律,第四个图形中y的值是.
三、解答题
-
16. 计算: .17. 先化简,再求值: ,其中x是从-1、0、1、2中选取一个合适的数.
18. 如图,在平行四边形 中,P是对角线 上的一点,过点C作 ,且 ,连接 , , .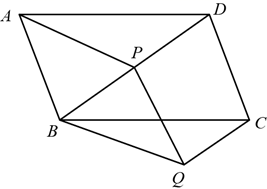 (1)、求证: ;(2)、若 ,求证:四边形 为菱形.19. 排球垫球是体育中考的项目之一,下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
(1)、求证: ;(2)、若 ,求证:四边形 为菱形.19. 排球垫球是体育中考的项目之一,下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
 (1)、运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为 , , ,如果在他们三人中选择一位垫球成绩较为稳定的接球能手作为自由人,则运动员更合适;(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(明树状图或列表法解答)20. 函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数 的图象,经历列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数 和 的图象如图所示.
(1)、运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)、经计算三人成绩的方差分别为 , , ,如果在他们三人中选择一位垫球成绩较为稳定的接球能手作为自由人,则运动员更合适;(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(明树状图或列表法解答)20. 函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数 的图象,经历列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数 和 的图象如图所示.x
…
-3
-2
-1
0
1
2
3
…
…
-6
-4
-2
0
-2
-5
-6
…
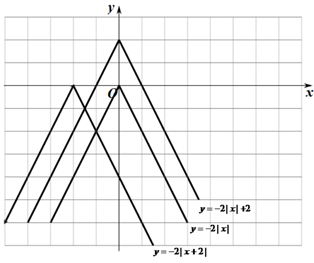 (1)、观察发现:函数 图象的顶点(最高点)坐标是 , 函数 图象的顶点坐标是 , 函数 图象的对称轴是.(2)、探索思考:平移函数 的图象是否可以得到函数 和 的图象?如果可以,分别写出平移的方向和距离.如果不行,请说明理由.(3)、拓展应用:在所给的平面直角坐标系内画出函数 的图象.若点( , )和( , )在该函数图象上,且 ,比较 , 的大小.21. 如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)、观察发现:函数 图象的顶点(最高点)坐标是 , 函数 图象的顶点坐标是 , 函数 图象的对称轴是.(2)、探索思考:平移函数 的图象是否可以得到函数 和 的图象?如果可以,分别写出平移的方向和距离.如果不行,请说明理由.(3)、拓展应用:在所给的平面直角坐标系内画出函数 的图象.若点( , )和( , )在该函数图象上,且 ,比较 , 的大小.21. 如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.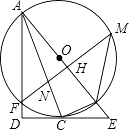 (1)、求证:AC平分∠DAE;(2)、若cosM= ,BE=1,①求⊙O的半径;②求FN的长.22. 已知A、B两地的高速公路总长为 ,货物运输车的行驶速度为 .(1)、若货物的公路运输费用包括运输成本和时间成本,已知某车货物从A地经高速公路运输到B地,运输成本为每千米2元,总运输费用为870元,那么它的时间成本是每小时多少元?(2)、“大升”快递公司有一批货物(不超过10车)需要先从A地经高速公路运输到B地,再从B地经铁路运输到C市,共需运费9720元.其中从A地到B地的每车运输费用与(1)相同,从B地到C市的铁路运输费用对不超过10车的货物计费为:一车900元,当货物增加一车时,每车的运费减少30元.问这批货物有几车?23. 在矩形 中,点E在 边上,P为线段 的中点,连接 、 .
(1)、求证:AC平分∠DAE;(2)、若cosM= ,BE=1,①求⊙O的半径;②求FN的长.22. 已知A、B两地的高速公路总长为 ,货物运输车的行驶速度为 .(1)、若货物的公路运输费用包括运输成本和时间成本,已知某车货物从A地经高速公路运输到B地,运输成本为每千米2元,总运输费用为870元,那么它的时间成本是每小时多少元?(2)、“大升”快递公司有一批货物(不超过10车)需要先从A地经高速公路运输到B地,再从B地经铁路运输到C市,共需运费9720元.其中从A地到B地的每车运输费用与(1)相同,从B地到C市的铁路运输费用对不超过10车的货物计费为:一车900元,当货物增加一车时,每车的运费减少30元.问这批货物有几车?23. 在矩形 中,点E在 边上,P为线段 的中点,连接 、 .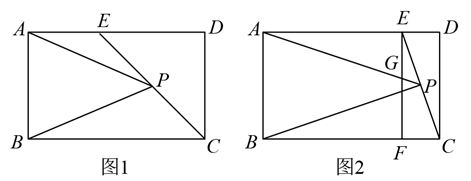 (1)、如图1,若 , ,求 的长;(2)、求证:无论点E在 上运动到何处, 一定是等腰三角形;(3)、如图2,过点E作 交 于点G,交 于点F.当 ,且 时,求 的长.24. 已知抛物线 有最低点为F.(1)、当抛物线经过点E(-1,3)时,①求抛物线的解析式;②点M是直线 下方抛物线上的一动点,过点M作平行于y轴的直线,与直线 交于点N,求线段 长度的最大值;(2)、将抛物线G向右平移m个单位得到抛物线 .经过探究发现,随着m的变化,抛物线 顶点的纵坐标y和横坐标x之间存在一个函数,求这个函数关系式,并写出自变量x的取值范围;(3)、记(2)所求的函数为H,抛物线G与函数H的交点为P,请结合图象求出点P的纵坐标的取值范围.
(1)、如图1,若 , ,求 的长;(2)、求证:无论点E在 上运动到何处, 一定是等腰三角形;(3)、如图2,过点E作 交 于点G,交 于点F.当 ,且 时,求 的长.24. 已知抛物线 有最低点为F.(1)、当抛物线经过点E(-1,3)时,①求抛物线的解析式;②点M是直线 下方抛物线上的一动点,过点M作平行于y轴的直线,与直线 交于点N,求线段 长度的最大值;(2)、将抛物线G向右平移m个单位得到抛物线 .经过探究发现,随着m的变化,抛物线 顶点的纵坐标y和横坐标x之间存在一个函数,求这个函数关系式,并写出自变量x的取值范围;(3)、记(2)所求的函数为H,抛物线G与函数H的交点为P,请结合图象求出点P的纵坐标的取值范围.