湖北省十堰市张湾区2021年数学初中毕业生适应性训练试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的数是A、-3 B、 C、0 D、2. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
 A、 B、 C、 D、3. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是( )A、
A、 B、 C、 D、3. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是( )A、 B、
B、 C、
C、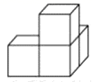 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 某同学对数据16,20,20,36,5■,51进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、平均数 C、方差 D、众数6. 为响应“科技扶贫”,我区某单位向一贫困村赠送1080本农村实用书籍,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱多用6个;已知每个B型包装箱比每个A型包装箱可少装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )A、 B、 C、 D、7. 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 某同学对数据16,20,20,36,5■,51进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、平均数 C、方差 D、众数6. 为响应“科技扶贫”,我区某单位向一贫困村赠送1080本农村实用书籍,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱多用6个;已知每个B型包装箱比每个A型包装箱可少装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )A、 B、 C、 D、7. 如图,小正方形的边长均为1,有格点△ABC,则sinC=( ) A、 B、 C、 D、8. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
A、 B、 C、 D、8. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )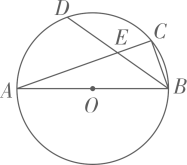 A、 B、 C、 D、9. 如图,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如图顺序依次排列为 , , , , , ,…,根据这个规律,第2021个点的坐标为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如图顺序依次排列为 , , , , , ,…,根据这个规律,第2021个点的坐标为( ) A、 B、 C、 D、10. 如图, 轴, 为垂足,双曲线 与 的两条边 , 分别相交于 , 两点, ,且 的面积为3,则 等于( )
A、 B、 C、 D、10. 如图, 轴, 为垂足,双曲线 与 的两条边 , 分别相交于 , 两点, ,且 的面积为3,则 等于( ) A、4 B、2 C、3 D、1
A、4 B、2 C、3 D、1二、填空题
-
11. 华为麒麟990芯片是目前市场运行速度最快的芯片,采用7纳米制造工艺,已知7纳米=0.000000007米,用科学记数法将0.000000007表示为.12. 如图,将△ABC的绕点A顺时针旋转得到△AED, 点D正好落在BC边上.已知∠C=80°,则∠EAB= °.
 13. 若2021m=6,2021n=4,则20212m﹣n=14. 若对于所有的实数 ,都有 ,则 .15. 如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为.
13. 若2021m=6,2021n=4,则20212m﹣n=14. 若对于所有的实数 ,都有 ,则 .15. 如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为. 16. 如图,正方形 的边长为2,点 ,点 分别是边 ,边 上的动点,且 , 与 相交于点 .若点 为边 的中点,点 为边 上任意一点,则 的最小值等于.
16. 如图,正方形 的边长为2,点 ,点 分别是边 ,边 上的动点,且 , 与 相交于点 .若点 为边 的中点,点 为边 上任意一点,则 的最小值等于.
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 .19. 某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用 , , , 表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)、请求出 班级作品件数,并估计全校共征集多少件作品?(2)、如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.20. 已知关于 的一元二次方程 ,其中 为常数.(1)、求证:无论 为何值,方程总有两个不相等实数根.(2)、已知函数 的图象不经过第三象限,求 的取值范围.21. 如图,在矩形 的 边上取一点E,连接 ,使得 ,在 边上取一点F,使得 ,连接 ,过点D作 于G.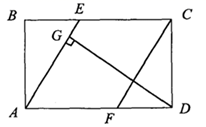 (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.22. 如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.22. 如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD. (1)、求证:CE是⊙O的切线;(2)、若⊙O的半径长为5,BF=2,求EF的长.23. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
(1)、求证:CE是⊙O的切线;(2)、若⊙O的半径长为5,BF=2,求EF的长.23. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.24. 如图,在 中, , ,点 , 分别在边 , 上, ,连接 、 ,点 为 的中点. (1)、观察图1,猜想线段 与 的数量关系是 , 位置关系是;(2)、把 绕点 逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立请证明;若不成立,请写出新的结论并说明理由;(3)、把 绕点 在平面内自由旋转,若 , ,请直接写出线段 长的取值范围.25. 已知:如图,抛物线y= x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)、观察图1,猜想线段 与 的数量关系是 , 位置关系是;(2)、把 绕点 逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立请证明;若不成立,请写出新的结论并说明理由;(3)、把 绕点 在平面内自由旋转,若 , ,请直接写出线段 长的取值范围.25. 已知:如图,抛物线y= x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
 (1)、求抛物线的解析式;(2)、若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;(3)、若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;(3)、若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.