湖北省安陆市云梦县等五县市2021年数学中考二模试卷

试卷更新日期：2021-09-16 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数5的相反数是（）

A、 $\frac{1}{5}$ B、5 C、 $- \frac{1}{5}$ D、-5

查看试题解析
2. 如图， $A B // C D$ ，点P为 $C D$ 上一点， $P E$ 平分 $∠ D P F$ ，若 $∠ 1 = 70 °$ ，则 $∠ 2$ 的大小为（）

A、50° B、55° C、60° D、65°

查看试题解析
3. 如图所示的几何体是由4个大小相同的小立方体搭成，其主视图是（）

A、 B、 C、 D、

查看试题解析
4. 在学校举行的“垃圾分类，人人有责”知识测试活动中，某小组的7名同学的测试成绩（单位：分）如下：90，80，90，85，85，90，95.则关于这组成绩数据，其众数和中位数分别是（）

A、85，90 B、90，85 C、90，90 D、85，85

查看试题解析
5. 根据圆规作图的痕迹，可用直尺成功地找到 $A B$ 边的中点的是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} - a^{2} = a$ C、 $a^{3} \cdot a^{2} = a^{6}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
7. 将抛物线 $y = (x + 1) (x + 3)$ 绕坐标原点O旋转180°，所得抛物线的解析式为（）

A、 $y = x^{2} - 4 x + 3$ B、 $y = - x^{2} + 4 x - 3$ C、 $y = - x^{2} + 4 x - 5$ D、 $y = x^{2} - 4 x + 5$

查看试题解析
8. 甲、乙两地之间是一条直路，在全民健身活动中，小明跑步从甲地前往乙地，一段时间后，小亮骑自行车从乙地前往甲地，两人都保持匀速.小亮先到达目的地，两人之间的距离y（km）与小明运动的时间t（h）的函数关系大致如图所示，则下列说法不正确的是（）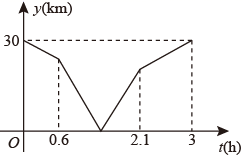

A、小明比小亮先出发36分钟 B、小明的速度为10km/h C、小亮的速度为20km/h D、小亮出发1h后与小明相遇

查看试题解析

二、填空题

9. 分解因式： $2 m^{2} - 18 =$ .

查看试题解析
10. 下列事件：①任意画一个三角形，其内角和为180°；②在平面内任意画两条直线，则其位置关系是相交；③掷一枚质地均匀的骰子，向上一面的点数是6.其中是随机事件的是.（填序号）

查看试题解析
11. 已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为

查看试题解析
12. 已知关于 $x$ 的方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则 $m$ 的值是..

查看试题解析
13. 如图，某海防哨所O发现在它的东南方向距离哨所1000m的A处有一艘轮船向正西方向航行，一段时间后，轮船到达哨所南偏西60°方向的B处，则此时这艘轮船与哨所的距离 $O B$ 约为m.（精确到1m， $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
14. 不等式组 ${\begin{array}{l} x - 4 < 0 \\ \frac{x + 5}{2} \geq 1 \end{array}$ 的所有整数解的和为.

查看试题解析
15. 如图，在四边形 $A B C D$ 中，连接 $B D$ ， $A B ⊥ B C$ ， $A D ⊥ B D$ ， $\tan ∠ B D C = 1$ .若 $A B = 15$ ， $B C = 10$ ，则 $B D =$ .

查看试题解析

三、解答题

16. 如图，已知菱形 $A B C D$ ，以 $A B$ 为直径作 $⊙ O$ ，与 $B C$ 交于点E， $A D = 6$ ， $∠ D = 30 °$ ，则图中阴影部分的面积为.

查看试题解析
17. 计算： $\sqrt{18} + {2.5}^{0} + | \sqrt{2} - 3 | - 2 \sin 45 °$ .

查看试题解析
18. 我国西汉时期张苍等人辑撰的《九章算术》是人类科学史上应用数学的“算经之首”，书中记载“今有三人共车，二车空；二人共车，九人步.问：人与车各几何?”，其意思是：“今有若干人准备乘若干辆马车出行，如果每3人共乘1辆车，则有2辆车空出；如果每2人共乘1辆车，则有9人需步行.问：人数和马车数各是多少?”.请你解答此问题.

查看试题解析
19. 某校为了响应市政府“创建文明城市”号召，依次开展了“A：文明礼仪，B：环境保护，C：垃圾分类，D：卫生保洁”四个主题的系列实践活动，每个学生选择一个主题参与活动.为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如下不完整的频数分布表和扇形统计图.

活动类别

频数

A

35

B

C

15

D

(1)、本次调查的学生人数是人， $m =$ ；

(2)、该校共有学生800人，试估计该校参加“垃圾分类”主题实践活动的学生约有多少人?

(3)、在本次系列主题活动中，某班有甲、乙、丙、丁四位同学表现特别优秀，现要从中随机选取两位同学分别参加学校的两项交流活动，求甲同学被选中的概率.

查看试题解析
20. 如图，已知 $△ A B C$ ，以 $A B$ 为直径的 $⊙ O$ 与 $B C$ 交于点D，与 $A C$ 交于点E.过点D作 $⊙ O$ 的切线正好与 $A C$ 垂直，垂足为点F.

(1)、求证： $A B = A C$ ；

(2)、若 $D F = 4$ ， $\tan ∠ A B C = 2$ ，求 $⊙ O$ 的半径.

查看试题解析
21. 如图，在平面直角坐标系中，直线 $y = x + 1$ 与x轴交于点A，与y轴交于点B，与双曲线 $y = \frac{k}{x}$ 在第一象限交于点C.点P为直线 $y = x + 1$ 上一点，过点P作x轴的垂线，垂足为点D，与双曲线交于点E， $P E = 2 D E$ ，连接 $B E$ ，且 $B E // x$ 轴.

(1)、求k的值；

(2)、求 $△ C P E$ 的面积.

查看试题解析

22. 某商场销售的一种商品的进价为30元/件，连续销售100天后，统计发现：在这100天内，①该商品每天的销售价格x（元/件）与时间（第1天）满足关系式：

x = {\begin{array}{l} t + 50 (1 \leq t < 60) \\ 110 (60 \leq t \leq 100) \end{array}

；

②该商品的日销售量y（件）与时间t（第t天）满足一次函数关系，部分数据如下表：

时间t（第t天）	1	2	10	20	……
日销售量y（件）	119	118	110	100	……

(1)、直接写出y与t之间的函数解析式：

(2)、设销售该商品的日利润为w（元），请直接写出w与t之间的函数解析式，并求出在这100天内哪天的日利润最大，最大日利润是多少元?

(3)、在这100天内，日利润不低于4000元的共有多少天，请直接写出结果.

查看试题解析

23. 已知 $O N ⊥ O M$ ， $△ A B C$ 的顶点A在 $O N$ 上，顶点B在 $O M$ 上，且 $C A = C B$ ， $C A ⊥ C B$ .连接 $O C$ ，与 $A B$ 交于点D.

(1)、如图1，若 $C A ⊥ O N$ ，求证： $O C$ 平分 $∠ M O N$ ；

(2)、如图2，若 $C A$ 与 $O N$ 不垂直， $O C$ 是否仍平分 $∠ M O N$ ?请作出结论，并说明理由

(3)、如图3，若 $\frac{O D}{C D} = \frac{1}{2}$ ， $B C = 6$ ，求 $A D$ 的长.

查看试题解析
24. 已知：抛物线 $y = - x^{2} + b x + c$ 经过点 $B (3 ， 0)$ 和 $C (0 ， 3)$ ，与x轴交于另一点A.

(1)、求抛物线的解析式；

(2)、如图1，连接 $A C$ ，作直线 $B C$ ，点P为直线 $B C$ 上方的抛物线上的点.
①当点P关于直线 $B C$ 的对称点 $P^{'}$ 恰好在坐标轴上时，求此时点P的坐标；

②如图2，过点P作 $A C$ 的平行线，与直线 $B C$ 交于点D.过点P作直线 $B C$ 的垂线，与直线 $B C$ 交于点E.求 $△ P D E$ 周长的最大值.

查看试题解析

活动类别	频数
A	35
B
C	15
D