河南省南阳市社旗县2021年数学中考二模试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. =( )A、 B、 C、2 D、-22. 我国渤海、黄海、东海、南海海水含有不少化学元素,其中铝、锰元素总量均约为 吨.用科学记数法表示铝、锰元素总量的和,接近值是( ).A、 B、 C、 D、3. 2020年4月7日,中国邮政发行了《众志成城 抗击疫情》邮票一套两枚(图1),以此纪念在抗击新冠肺炎疫情的过程中,中国人民所展现出的“中国精神、中国力量、中国担当”.两枚邮票用一个“众”字型的背景图案巧妙相连,从几何的角度看,这个图案(图2)( )
 A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形4. 下列说法正确的是( )A、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖. B、对某池塘中现有鱼的数量的调查,最适合采用全面调查. C、“任意画一个三角形,其内角和是 ”这个事件是必然事件. D、对角线相等的四边形是矩形.5. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形4. 下列说法正确的是( )A、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖. B、对某池塘中现有鱼的数量的调查,最适合采用全面调查. C、“任意画一个三角形,其内角和是 ”这个事件是必然事件. D、对角线相等的四边形是矩形.5. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )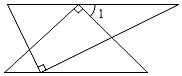 A、30° B、45° C、55° D、60°6. 下列各式计算正确的是( )A、 B、 C、 D、7. 能说明命题“关于 的方程 一定有实根”是假命题的反例为( )A、 B、 C、 D、8. 已知点 , , 在反比例函数 的图象上,若 ,则 , 的大小关系是( )A、 B、 C、 D、 , 的大小不确定9. 如图,已知平行四边形 的顶点 , , , ,点 在 轴正半轴上,按以下步骤作图:①分别以点 , 为圆心,以大于 的长为半径画弧,两弧相交于点 , ;②连接 ,交 于点 ,交 轴于点 ,则点 的坐标为( )
A、30° B、45° C、55° D、60°6. 下列各式计算正确的是( )A、 B、 C、 D、7. 能说明命题“关于 的方程 一定有实根”是假命题的反例为( )A、 B、 C、 D、8. 已知点 , , 在反比例函数 的图象上,若 ,则 , 的大小关系是( )A、 B、 C、 D、 , 的大小不确定9. 如图,已知平行四边形 的顶点 , , , ,点 在 轴正半轴上,按以下步骤作图:①分别以点 , 为圆心,以大于 的长为半径画弧,两弧相交于点 , ;②连接 ,交 于点 ,交 轴于点 ,则点 的坐标为( )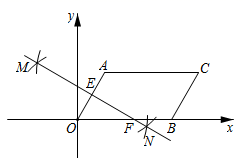 A、 B、 C、 D、10. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )
A、 B、 C、 D、10. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )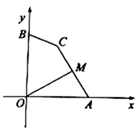 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若分式 的值为0,则 的值为.12. 不等式组 的最小整数解是 .
13. 二十四节气列入联合国教科文组织人类非物质文化遗产代表作名录.太阳运行的轨道是一个圆形,古人将之称作“黄道”,并把黄道分为24份,每15度就是一个节气,统称“二十四节气”.这一时间认知体系被誉为“中国的第五大发明”.如图,指针落在惊蛰、春分、清明区域的概率是. 14. 某种商品的商标图案如图所示(阴影部分),已知菱形 的边长为4, ,弧 是以 为圆心, 长为半径的弧,弧 是以B圆心,BC长为半径的弧,则该商标图案(阴影部分)的面积为.
14. 某种商品的商标图案如图所示(阴影部分),已知菱形 的边长为4, ,弧 是以 为圆心, 长为半径的弧,弧 是以B圆心,BC长为半径的弧,则该商标图案(阴影部分)的面积为. 15. 如图,在矩形 中, , , 、 分别为 、 边上的点,且 , 为 上一点,且 , 、 分别为 、 的中点,则 .
15. 如图,在矩形 中, , , 、 分别为 、 边上的点,且 , 为 上一点,且 , 、 分别为 、 的中点,则 .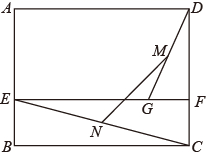
三、解答题
-
16. 如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.
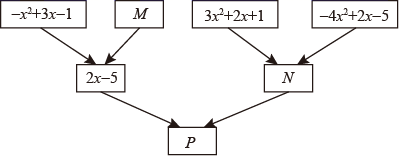 (1)、求整式 .(2)、先求整式 ,再自选一个喜欢的 值代入求出 值.17. 截止到2020年11月,我国贫困县“摘帽”计划已经全部完成,脱贫攻坚取得了全面胜利!为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对名省贫困地区的持续投入,小凯同学通过登录国家乡村振兴局网站,查询到了2020年中央财政脱贫专项资金对我国28个省、直辖市、自治区的分配额度(亿元),并对数据进行整理、描述和分析.下面是小凯给出的部分信息.
(1)、求整式 .(2)、先求整式 ,再自选一个喜欢的 值代入求出 值.17. 截止到2020年11月,我国贫困县“摘帽”计划已经全部完成,脱贫攻坚取得了全面胜利!为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对名省贫困地区的持续投入,小凯同学通过登录国家乡村振兴局网站,查询到了2020年中央财政脱贫专项资金对我国28个省、直辖市、自治区的分配额度(亿元),并对数据进行整理、描述和分析.下面是小凯给出的部分信息.a.反映2020年中央财政脱贫专项资金分配额度的频数分布直方图如下(数据分成8组: , , , , , , , )
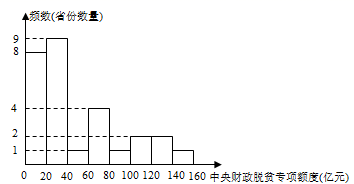
b.2020年中央财政脱贫专项资金在 这一组分配的额度是(亿元):
25;28;28;30;37;37;38;39;39
(1)、2020年中央财政脱贫专项资金对各省、直辖市、自治区分配额度的中位数为(亿元);(2)、2020年中央财政脱贫专项资金对某省的分配额度为95亿元,该额度在28个省、直辖市、自治区中由高到低排第名;(3)、小凯在收集数据时得到了2016-2020年中央财政脱贫专项资金对自治区A和自治区B的分配额度变化图: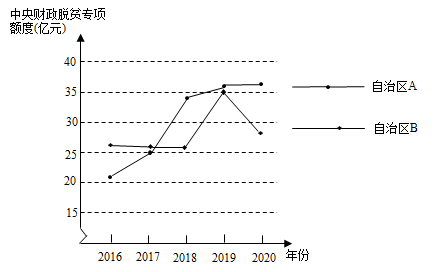
①比较2016年-2020年中央财政脱贫专项资金对自治区A,B的分配额度,方差 ▲ _ (填写“>”或者“<”);
②请结合统计数据,针对中央财政脱贫专项资金对自治区A,B脱贫攻坚工作的支持情况,说一说你的看法.
18. 小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)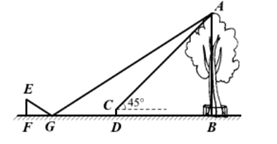 19. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后价格调为8.1元/斤,并且两次降价的百分率相同.
19. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后价格调为8.1元/斤,并且两次降价的百分率相同.时间 (天)
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
储存和损耗费用(元)
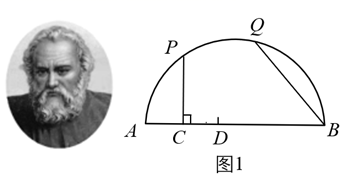
(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第 天( 为整数)的售价、销量及储存和损耗费用的相关信息如表所示;已知该种水果的进价为4.1元/斤,设销售该水果第 天的利润为 元,求 与 之间的函数关系式,并求出第几天时销售利润最大?20. 请阅读以下材料,并完成相应的任务.在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:如图1,点 是 上的任意一点, 于点 ,点 在弦 上且 ,在 上取一点 ,使 ,连接 ,则有 .
 (1)、如图2,小明同学尝试说明“ ”,于是他连接了 , , , ,请根据小明的思路完成后续证明过程;
(1)、如图2,小明同学尝试说明“ ”,于是他连接了 , , , ,请根据小明的思路完成后续证明过程;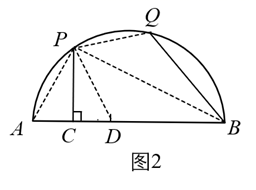 (2)、如图3,以 为直径的半圆上有一点 , , ,直线 与 相切于点 ,过点 作 于点 ,交 于点 ,则 .
(2)、如图3,以 为直径的半圆上有一点 , , ,直线 与 相切于点 ,过点 作 于点 ,交 于点 ,则 .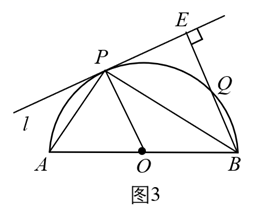 21. 如图,抛物线 过 , , 三点,边长为4的正方形 的顶点 , 分别在 轴上, 轴上.
21. 如图,抛物线 过 , , 三点,边长为4的正方形 的顶点 , 分别在 轴上, 轴上.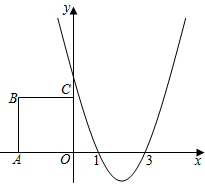 (1)、求抛物线解析式,并直接写出当 时 的最大值与最小值的差.(2)、将正方形 向右平移,平移距离记为 .
(1)、求抛物线解析式,并直接写出当 时 的最大值与最小值的差.(2)、将正方形 向右平移,平移距离记为 .①当点 首次落在抛物线上,求 的值.
②当抛物线落在正方形内的部分,满足 随 的增大而减小时,请直接写出 的取值范围.
22. 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
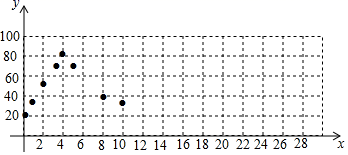
下面是小明的探究过程,请补充完整:
(1)、下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况接通电源后的时间x(单位:min)
0
1
2
3
4
5
8
10
16
18
20
21
24
32
…
水箱中水的温度y(单位:℃)
20
35
50
65
80
64
40
32
20
m
80
64
40
20
…
m的值为;
(2)、①当0≤x≤4时,写出一个符合表中数据的函数解析式 ▲ ;当4<x≤16时,写出一个符合表中数据的函数解析式 ▲ ;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)、如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min.23. 在矩形 的 边上取一点 ,将 沿 翻折,使点 恰好落在 边上点 处.(1)、如图1,若 ,求 的度数;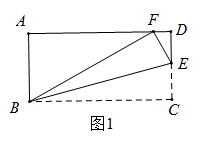 (2)、如图2,当 ,且 时,求 的长;
(2)、如图2,当 ,且 时,求 的长;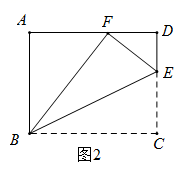 (3)、如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 出的值.
(3)、如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 出的值.