河南省洛阳市涧西区2021年数学中考三模试卷

试卷更新日期：2021-09-16 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{2}{5}$ 的倒数是（）

A、0.4 B、2.5 C、4 D、 $- \frac{2}{5}$

查看试题解析
2. 中国首次火星探测任务天问一号探测器在2021年2月10日成功被火星捕获，成为中国第一颗人造火星卫星，并在距离火星约11000米处，拍摄了火星全景图象.将11000用科学记数法表示应为（）

A、 $11 \times 10^{3}$ B、 $1 .1 \times 10^{5}$ C、 $1 .1 \times 10^{4}$ D、 $0.11 \times 10^{5}$

查看试题解析
3. 如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正方形中数字表示该位置小正方体的个数，则该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图， $A B / / C D ， ∠ A = 100 ° ， ∠ B C D = 50 ° ， ∠ A C B$ 的度数为（）

A、 $25 °$ B、 $30 °$ C、 $45 °$ D、 $50 °$

查看试题解析
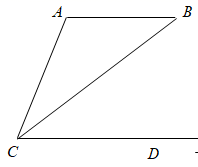5. 下列采用的调查方式中，不合适的是（）

A、了解洛河水的水质，采用抽样调查 B、了解洛阳市中学生睡眠时间，采用抽样调查 C、了解一批灯泡的使用寿命，采用全面调查 D、了解某个班级学生的数学成绩，采用全面调查

查看试题解析
6. 若点 $A (x_{1} ， - 4)$ ， $B (x_{2} ， 2)$ ， $C (x_{3} ， 3)$ 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{1} > x_{3} > x_{2}$ C、 $x_{3} > x_{2} > x_{1}$ D、 $x_{2} > x_{3} > x_{1}$

查看试题解析
7. 定义 $a ★ b = a^{2} + a (b - 2) + 4$ ，例如 $3 ★ 7 = 3^{2} + 3 \times (7 - 2) + 4 = 28$ ，若方程 $x ★ m = 0$ 的一个根是 $- 1$ ，则此方程的另一个根是（）

A、-2 B、-3 C、-4 D、-5

查看试题解析
8. 《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安.今乙发已先二日，甲乃发长安.问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安.现乙先出发2日，甲才从长安出发.问甲出发几日，甲乙相逢？设甲出发x日，甲乙相逢，可列方程（）

A、 $\frac{7}{x + 2} + \frac{5}{x} = 1$ B、 $\frac{7}{x + 2} - \frac{5}{x} = 1$ C、 $\frac{x + 2}{7} + \frac{x}{5} = 1$ D、 $\frac{x + 2}{7} = \frac{x}{5}$

查看试题解析
9. 如图，在平面直角坐标系中，矩形 $A B C D$ 的边 $B C$ 在 $x$ 轴上，顶点 $A (- 2 ， 3)$ ， $C (2 ， 0)$ ，连接 $A C$ ，按下列方法作图：

（1）以点 $C$ 为圆心，适当长为半径画弧，分别交 $C A$ 、 $C D$ 于点 $E$ ， $F$ ；
（2）分别以点 $E$ ， $F$ 为圆心，大于 $\frac{1}{2} E F$ 的长为半径画弧两弧交于点 $G$ ；
（3）作射线 $C G$ 交 $A D$ 于点 $H$ ，则点 $H$ 的横坐标为（）
A. $\frac{1}{2}$
B. $\frac{3}{4}$
C.1
D. $\frac{3}{2}$

查看试题解析
10. 如图①，在菱形 $A B C D$ 中， $∠ D = 120 °$ ，点 $E$ 是 $A B$ 的中点，点 $P$ 是对角线 $A C$ 上一动点，设 $P C$ $= x$ ， $P E + P B = y$ ，图②是 $y$ 关于 $x$ 的函数图象，且图象上最低点 $Q$ 的坐标为 $(\frac{8 \sqrt{3}}{3} ， 2 \sqrt{3})$ ，则菱形 $A B C D$ 的边长为（）

A、2 B、 $\frac{3 \sqrt{3}}{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析

二、填空题

11. 比 $\sqrt{7}$ 大的整数中，最小的是．

查看试题解析
12. 不等式组 ${\begin{matrix} 1 - x \leq 0 \\ \frac{3 x + 1}{2} > x \end{matrix}$ 的解集为.

查看试题解析
13. 一个不透明的口袋中有四张卡片，上面分别写着数字1，2，3，4，除数字外四张卡片无其他区别，随机从这个口袋中同时取出两张卡片，卡片上的数字之和大于5的概率是

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A = 90 °$ ， $B C = 2 A C$ ，以点 $A$ 为圆心的弧与 $B C$ 相切于点 $F$ ，分别交 $A B$ 、 $A C$ 于点 $D$ 、 $E$ ，若 $C F = 1$ ，则图中阴影部分的面积为.（结果保留 $π$ ）

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A E = D E = 3$ ，连接 $C E$ ，点 $F$ 是 $C E$ 上一点，且 $E F = 2 C F$ ，连接 $B F$ ，点 $M$ 是 $B F$ 的中点，过点 $M$ 作 $M N ⊥ B C$ 于点 $N$ ，连接 $F N$ ，则 $F N$ 的长为.

查看试题解析

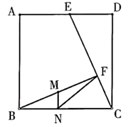
三、解答题

16. 下面是小林同学进行分式化简的过程，请认真阅读并完成相应任务.
$\frac{x^{2} - 16}{x^{2} + 8 x + 16} - \frac{2 x + 1}{2 x + 8}$

$= \frac{(x + 4) (x - 4)}{{(x + 4)}^{2}} - \frac{2 x + 1}{2 (x + 4)}$ 第一步

$= \frac{x - 4}{x + 4} - \frac{2 x + 1}{2 (x + 4)}$ 第二步

$= \frac{2 (x - 4)}{2 (x + 4)} - \frac{2 x + 1}{2 (x + 4)}$ 第三步

$= \frac{2 x - 8 - (2 x + 1)}{2 (x + 4)}$ 第四步

$= \frac{2 x - 8 - 2 x + 1}{2 (x + 4)}$ 第五步

$= - \frac{7}{2 x + 8}$ 第六步

任务一：填空：

①从上面的化简步骤，第 ▲ 步是进行分式的通分，通分的依据是 ▲ .

②第 ▲ 步开始出现错误，这一步错误的原因是 ▲ .

任务二：请写出这道题正确的化简过程.

查看试题解析
17. 为迎接2022年冬奥会，鼓励更多的学生参与到志愿服务中去，甲、乙两所学校组织了志愿服务团队选拔活动，经过初选，两所学校各有400名学生进入综合素质展示环节，为了了解两所学校这些学生的整体情况，从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如图：

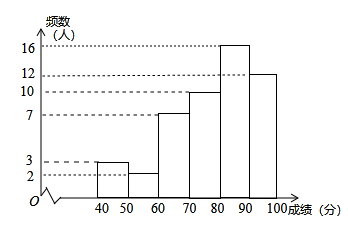
（数据分成6组： $40 \leq x < 50$ ， $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x < 100$ ）.

b.甲学校学生成续在 $80 \leq x < 90$ 这一组的是：

80 80 81 81.5 82 83 83 84 85 86 86.5 87 88 88.5 89 89

c.乙学校学生成绩的平均数、中位数、众数、优秀率（85分及以上为优秀）如下：

平均数

中位数

众数

优秀率

83.3

84

78

46%

根据以上信息，回答下列问题

(1)、甲学校学生 $A$ ，乙学校学生 $B$ 的综合素质展示成绩同为83分，这两人在本校学生中综合素质展示排名更靠前的是（填“A”或“B”）；

(2)、若两所学校的平均数相同，根据上述信息，推断哪所学校综合素质展示的水平更高，并说明理由（从两个不同的角度说明推断的合理性）.

(3)、若每所学校综合素质展示的前120名学生将被选入志愿服务团队，预估甲学校分数至少达到分的学生才可以入选.

查看试题解析
18. 如图，在东西方向的海岸上有两个相距6海里的码头B，D．某海岛上的观测塔A距离海岸5海里，在A处测得B位于南偏西 $22 °$ 方向．一艘渔船从D出发，沿正北方向航行至C处，此时在A处测得C位于南偏东 $67 °$ 方向，求此时观测塔A与渔船C之间的距离（结果精确到0.1海里）．
（参考数据： $\sin 22^{o} \approx \frac{3}{8}$ ， $\cos 22 ° \approx \frac{15}{16}$ ， $\tan 22 ° \approx \frac{2}{5}$ ， $\sin 67^{°} \approx \frac{12}{13}$ ， $\cos 67 ° \approx \frac{5}{13}$ ， $\tan 67 ° \approx \frac{12}{5}$ ）

查看试题解析
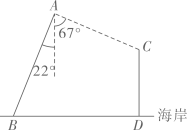19. 某大型商场为了提高销售人员的积极性，对原有的薪酬计算方式进行了修改，设销售人员一个月的销售量为 $x$ （件），销售人员的月收入为 $y$ （元），原有的薪酬计算方式 $y_{1}$ 元采用的是底薪+提成的方式，且 $y_{1} = k_{1} x + b$ ，已知每销售一件商品另外获得15元的提成修改后的薪酬计算方式为 $y_{2}$ （元），且 $y_{2} = k_{2} x + b$ ，根据图象回答下列问题：

(1)、求 $y_{1}$ 和 $y_{2}$ 的解析式，并说明 $b$ 的实际意义；

(2)、求两个函数图象的交点 $F$ 的坐标，并说明交点 $F$ 的实际意义；

(3)、根据函数图象请判断哪种薪酬计算方式更适合销售人员.

查看试题解析
20. 请阅读下列材料，并完成相应的任务.
阿基米德折弦定理

阿基米德（Archimedes，公元前287~公元212年，古希腊是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子.

阿拉伯Al-Biruni（973年-1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理.

阿基米德折弦定理：如图1， $A B$ 和 $B C$ 是 $⊙ O$ 的两条弦（即折线 $A B C$ 是圆的一条折弦）， $A B > B C$ ， $D$ 是 $\overset{⌢}{A B C}$ 的中点，则从点 $D$ 向 $A B$ 所作垂线的垂足 $E$ 是折弦 $A B C$ 的中点，即 $A E = E B + B C$ ，

下面是运用“补短法”证明 $A E = E B + B C$ 的部分证明过程.

证明：如图2，延长 $C B$ 到点F，使得 $C F = A E$ ，连接DA，DB，DC和DF.

∵ $D$ 是 $\overset{⌢}{A B C}$ 的中点

∴ $D A = D C$

…

任务：

(1)、请按照上面的证明思路，写出该证明的剩余部分：

(2)、填空：如图3，已知等边 $△ A B C$ 内接于 $⊙ O$ ， $A B = 6$ ， $D$ 为 $⊙ O$ 上一点， $∠ A B D = 45 °$ . $A E ⊥ B D$ 于点 $E$ ，则 $△ B D C$ 的周长是.

查看试题解析
21. 二次函数 $y = m x^{2} - 2 m x - m + 3$ .

(1)、求该二次函数的对称轴；

(2)、过动点 $C (0 ， n)$ 作直线 $a ⊥ y$ 轴，当直线 $a$ 与抛物线只有一个公共点时，求 $n$ 关于 $m$ 的函数表达式；

(3)、若对于每一个 $x$ 值，它所对应的函数值都不小于1，求整数 $m$ 的值.

查看试题解析

22. 小亮在学习中遇到如下一个问题：

如图1，点 $C$ 是半圆 $A m B$ 上一动点，线段AB=6，CD平分 $∠ A C B$ ，过点 $A$ 作 $A D // B C$ 交 $C D$ 于点 $D$ ，连接 $B D$ .当 $△ B C D$ 为等腰三角形时，求线段 $A C$ 的长度.

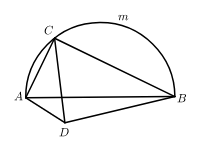
小亮分析发现，此问题很难通过常规的推理计算彻底解决，于是他尝试结合学习函数的经验研究此问题.将线段 $A C$ 的长度作为自变量 $x$ ， $B C$ ， $B D$ 和 $C D$ 的长度都是 $x$ 的函数，分别记为 $y_{B C}$ ， $y_{B D}$ 和 $y_{C D}$ .请将下面的探究过程补充完整：

(1)、根据点

C

在半圆

A m B

上的不同位置，画出相应的图形，测量线段

A C

，

B C

，

B D

的长度，得到下表的几组对应值：

$A C$	0	1.0	2.0	3.0	4.0	4.5	5.0	5.5	6
$B C$	6	5.9	5.7	5.2	4.5	a	3.3	2.4	0
$B D$	6	5.0	4.2	3.7	4	4.5	5.3	6.3	8.5

①上表中 $a$ 的值是 ▲

②操作中发现，“无需测量线段 $C D$ 的长度即可得到 $y_{C D}$ 关于 $x$ 的函数解析式”.请直接写出 $y_{C D}$ 关于 $x$ 的函数解析式.

(2)、小亮已在平面直角坐标系

x O y

中画出了函数

y_{B D}

的图象，如图2所示.

①请在同一个坐标系中画出函数 $y_{B C}$ 和 $y_{C D}$ 的图象；

②结合图象直接写出当 $△ B C D$ 为等腰三角形时，线段 $A C$ 长度的近似值（结果保留一位小数）.

查看试题解析

23. 在 $R t △ A B C$ 中， $A B = A C = 3$ ， $∠ B A C = 90 °$ ，点 $D$ 为边 $B C$ 的中点，以 $C D$ 为一边作正方形 $C D E F$ ，

(1)、如图1，点E恰好与点A重合，则线段BE与AF的数量关系为；

(2)、在（1）的条件下，
①如果正方形 $C D E F$ 绕点 $C$ 旋转，连接 $B E$ 、 $C E$ 、 $A F$ ，线段 $B E$ 与AF的数量关系有无变化？请仅就图2的情形给出证明；

②正方形 $C D E F$ 绕点 $C$ 旋转的过程中，当以点A，B，C，E为顶点的四边形是平行四边形时.直接写出线段AF的长.

查看试题解析

平均数	中位数	众数	优秀率
83.3	84	78	46%