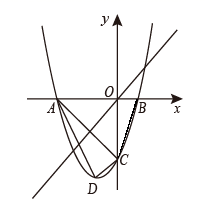
广西贵港市2021年初中毕业班数学第二次教学质量监测试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. -2021的绝对值是( )A、 B、 C、-2021 D、20212. 一组数据1,1,3,2,2,0的众数是( )A、1 B、1.5 C、2 D、1和23. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 植物学家在厄瓜多尔意外地发现了一种兰花新物种,是兰花物种中最小的一种,花瓣直径仅2.1毫米,把2.1毫米用科学记数法表示为 米,则 的值为( )A、-4 B、-3 C、-2 D、-16. 下列命题是真命题的是( )A、正六边形的内角和为 B、如果 ,那么 , C、内错角相等 D、 的算术平方根是47. 若关于 的一元二次方程 有实数根,则 的取值范围为( )A、 B、 C、 D、8. 如图,在 中, , , 的垂直平分线 交 于点 ,交 于点 ,若 ,则 的长为( )
 A、5 B、8 C、10 D、9. 如图, 是 的直径,点 , 在圆上, ,则 等于( )
A、5 B、8 C、10 D、9. 如图, 是 的直径,点 , 在圆上, ,则 等于( ) A、 B、 C、 D、10. 如图, 的顶点在正方形网格的格点上,则 的值为( )
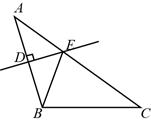
A、 B、 C、 D、10. 如图, 的顶点在正方形网格的格点上,则 的值为( )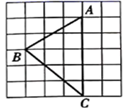 A、 B、 C、 D、11. 如图,在平行四边形ABCD中,AB=3,AD=5,AE平分∠BAD,交BC于F,交DC延长线于E,则 的值为( )
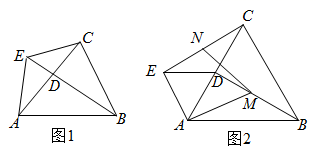
A、 B、 C、 D、11. 如图,在平行四边形ABCD中,AB=3,AD=5,AE平分∠BAD,交BC于F,交DC延长线于E,则 的值为( ) A、 B、 C、 D、212. 如图,菱形 的边长为4, , 分别是 , 边上的动点, , ,则下列结论:① ;② 为等边三角形;③ ;④若 ,则 .其中正确个数为( )
A、 B、 C、 D、212. 如图,菱形 的边长为4, , 分别是 , 边上的动点, , ,则下列结论:① ;② 为等边三角形;③ ;④若 ,则 .其中正确个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
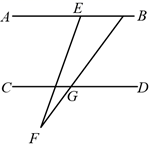
13. 计算: .14. 因式分解: .15. 如图,直线 ,若 , ,则 的度数为.
 16. 在一个不透明的袋子里,放着标有数字2、5、7、8的四个小球(除数字不同外,其余都相同),在看不见的情况下随机摸出2个球,则摸出的两个球上的数字的和不小于10的概率是.17. 如图,一张扇形纸片的圆心角为 ,半径为6.将这张扇形纸片折叠,使点 与点 恰好重合,折痕为 ,则阴影部分的面积为.
16. 在一个不透明的袋子里,放着标有数字2、5、7、8的四个小球(除数字不同外,其余都相同),在看不见的情况下随机摸出2个球,则摸出的两个球上的数字的和不小于10的概率是.17. 如图,一张扇形纸片的圆心角为 ,半径为6.将这张扇形纸片折叠,使点 与点 恰好重合,折痕为 ,则阴影部分的面积为.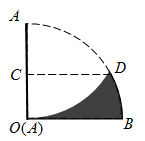 18. 下列关于二次函数 ( 为常数)的结论:
18. 下列关于二次函数 ( 为常数)的结论:①该函数的图象与函数 的图象的对称轴相同;
②该函数的图象的顶点在函数 的图象上;
③该函数的图象与 轴有交点时, ;
④点 与点 在该函数的图象上.
若 , ,则 .
其中正确的结论是(填写序号).
三、解答题
-
19.(1)、计算: .(2)、解分式方程: .20. 如图,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
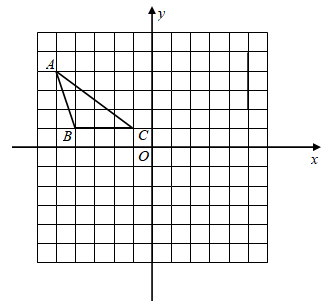
( 1 )作出 关于 轴对称的 .
( 2 )作出 绕点 按顺时针方向旋转90°得到的 .
21. 如图,直线 与双曲线 交于 , 两点,与 轴, 轴分别交于 , 两点,且 .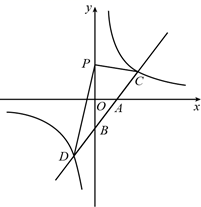 (1)、求一次函数和反比例函数的解析式.(2)、将点 沿 轴平移得到点 ,若 的面积为36,求点 的坐标.22. “读书对于智慧,就像体操对于身体一样.”某中学积极开展活动,鼓励全校师生利用课余时间进行体育锻炼和阅读.该校为了了解全校学生课外阅读情况,随机抽取了部分学生进行每周用于课外阅读时间的调查,根据调查结果绘制了如下统计表与扇形统计图.
(1)、求一次函数和反比例函数的解析式.(2)、将点 沿 轴平移得到点 ,若 的面积为36,求点 的坐标.22. “读书对于智慧,就像体操对于身体一样.”某中学积极开展活动,鼓励全校师生利用课余时间进行体育锻炼和阅读.该校为了了解全校学生课外阅读情况,随机抽取了部分学生进行每周用于课外阅读时间的调查,根据调查结果绘制了如下统计表与扇形统计图.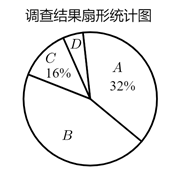
调查结果统计表
阅读时间(分钟)
等级
人数
16
2
根据上面的信息解答下列问题.
(1)、这次被调查的学生共有人, , .(2)、求扇形统计图中等级“ ”所对圆心角的度数.(3)、若该学校现有学生1000人,请你估计全校等级为“ ”的学生人数.(4)、若被抽取的学生每周平均阅读时间为60分钟,假设平均阅读一本课外书的时间为240分钟,请你估计该校学生每人一年(按52周计算)平均阅读课外书的数量.23. 《孙子算经》是中国古代的数学著作,成书大约一千五百年前.卷中举例说明筹算分数算法和筹算开平方法,其中“物不知数”的问题.在西方的数学史里被称为“中国的剩余定理”.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,向木条长多少尺?”24. 如图,在 中, , , ,以 为直径作 ,与 交于点 , 是 的中点,连接 ,连接 并延长交 的延长线于点 ,连接 交 于点 ,连接 . (1)、求证: 为 的切线.(2)、若 ,求 的长.
(1)、求证: 为 的切线.(2)、若 ,求 的长.