甘肃省酒泉市2021年数学中考二模试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的数是( )A、-3 B、0 C、1 D、22. 如图,有一块含有 角的直角三角板的两个顶点放在直尺的对边上.如果 ,那么 的度数是( )
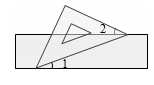 A、 B、 C、 D、3. 以下调查中,最适合抽样调查的是( )A、调查一批防疫口罩的质量 B、调查旅客随身携带的违禁物品 C、了解某班级学生的视力情况 D、在“新冠肺炎”疫情期间,对某校到校学生进行体温检测4. 下列四个几何体中,主视图是三角形的是( )A、
A、 B、 C、 D、3. 以下调查中,最适合抽样调查的是( )A、调查一批防疫口罩的质量 B、调查旅客随身携带的违禁物品 C、了解某班级学生的视力情况 D、在“新冠肺炎”疫情期间,对某校到校学生进行体温检测4. 下列四个几何体中,主视图是三角形的是( )A、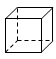 B、
B、 C、
C、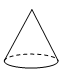 D、
D、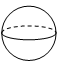 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )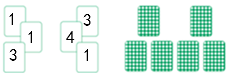 A、 B、 C、 D、7. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、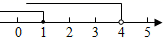 C、
C、 D、
D、 9. 如图,已知 和 的相似比是 ,且 的面积是1,则四边形 的面积是( )
9. 如图,已知 和 的相似比是 ,且 的面积是1,则四边形 的面积是( )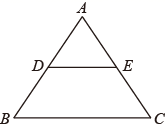 A、2 B、3 C、4 D、510. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( )
A、2 B、3 C、4 D、510. 如图,在 中, , , 于点D.点 从点A出发,沿 的路径运动,运动到点C停止,过点 作 于点E,作 于点F.设点P运动的路程为x,四边形 的面积为y,则能反映y与x之间函数关系的图象是( ) A、
A、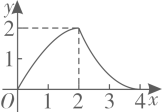 B、
B、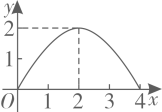 C、
C、 D、
D、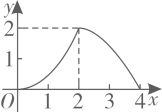
二、填空题
-
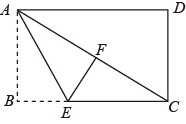
11. 分解因式: = .12. 若代数式 在实数范围内有意义,则x的取值范围是 .13. 如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是.
 14. 已知关于x的一元二次方程 有一个根为 ,则a的值为 .15. 如图,点A,B,C在圆O上,∠ACB=54°,则∠ABO的度数是.
14. 已知关于x的一元二次方程 有一个根为 ,则a的值为 .15. 如图,点A,B,C在圆O上,∠ACB=54°,则∠ABO的度数是.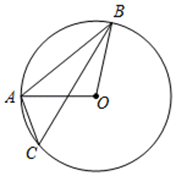 16. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x﹣1)※x的结果为 .17. 如图,在扇形OAB中,已知∠AOB=90°,OA= ,过弧AB的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为.
16. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x﹣1)※x的结果为 .17. 如图,在扇形OAB中,已知∠AOB=90°,OA= ,过弧AB的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为.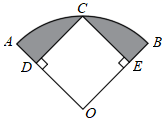 18. 已知函数 ,其中 表示当 时对应的函数值,如 , , ,…, ,则 .
18. 已知函数 ,其中 表示当 时对应的函数值,如 , , ,…, ,则 .三、解答题
-
19. 计算: .20. 解方程组:21. 利用尺规作 的平分线(如图).
已知: .
求作:射线 ,使 .
作法:①在 和 上分别截取 , ,使 .
②分别以 , 为圆心、以大于 的长为半径作弧,两弧在 内交于点 .
③作射线 . 就是 的平分线.
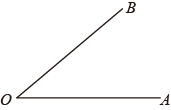
请你根据提供的材料完成下列问题:
(1)、根据作法补全图形(保留作图痕迹);(2)、这种作已知角平分线的方法的依据是(填序号).①SSS②SAS③AAS④ASA
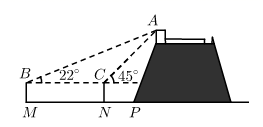
(3)、请你证明 为 的平分线.22. 酒泉老城区的西南隅,耸立着一座古城门——晋城门,它是东晋时期酒泉郡治驻地福禄县城的南门.某校数学社团的同学们使用卷尺和自制的测角仪测量晋城门的高度(如图).他们在地面一条水平道路 上架设测角仪,先在点 处测得晋城门最高点 的仰角为 ,然后沿 方向前进16m到达点 处,测得点 的仰角为 .测角仪的高度为1.6m.
 (1)、求晋城门最高点 距离地面的高度(结果精确到0.1m.参考数据: , , , );(2)、“景点简介”显示,晋城门的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花20元,购买A型、B型垃圾桶各花费了1000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共60个,要使总费用不超过2000元,最少要购买多少个A型垃圾桶?24. 知往鉴今,以启未来.在中国共产党成立100周年之际,重温党的历史,无论是对过去、现在还是将来,都具有重大而深远的意义.某校响应党总支号召,耕读党史故事,体味红色历程,开展了“学党史、感党恩、跟党走”的主题知识竞赛,全校同学均参与了此次竞赛.为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图(如图).
(1)、求晋城门最高点 距离地面的高度(结果精确到0.1m.参考数据: , , , );(2)、“景点简介”显示,晋城门的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.23. 生活垃圾处理是关系民生的基础性公益事业,加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任,某小区购进A型和B型两种分类垃圾桶,已知购买一个B型垃圾桶比购买一个A型垃圾桶多花20元,购买A型、B型垃圾桶各花费了1000元,且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍.(1)、求购买一个A型垃圾桶和一个B型垃圾桶各需多少元?(2)、若小区一次性购买A型和B型垃圾桶共60个,要使总费用不超过2000元,最少要购买多少个A型垃圾桶?24. 知往鉴今,以启未来.在中国共产党成立100周年之际,重温党的历史,无论是对过去、现在还是将来,都具有重大而深远的意义.某校响应党总支号召,耕读党史故事,体味红色历程,开展了“学党史、感党恩、跟党走”的主题知识竞赛,全校同学均参与了此次竞赛.为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图(如图).
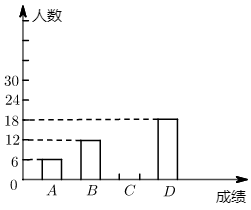 (1)、求被抽取的学生成绩在C: 组的有多少人;(2)、所抽取学生成绩的中位数落在哪个组内;(3)、若该学校有1500名学生,估计这次竞赛成绩在A: 组的学生有多少人.25. 已知反比例函数 的图象与一次函数 的图象交于点 和 .
(1)、求被抽取的学生成绩在C: 组的有多少人;(2)、所抽取学生成绩的中位数落在哪个组内;(3)、若该学校有1500名学生,估计这次竞赛成绩在A: 组的学生有多少人.25. 已知反比例函数 的图象与一次函数 的图象交于点 和 .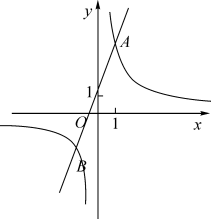 (1)、求这两个函数的关系式;(2)、如果点 与点 关于 轴对称,求 的面积.26. 如图, 为 的直径,C为 上的一点,AD与过点C的直线互相垂直,垂足为D,AC平分 .
(1)、求这两个函数的关系式;(2)、如果点 与点 关于 轴对称,求 的面积.26. 如图, 为 的直径,C为 上的一点,AD与过点C的直线互相垂直,垂足为D,AC平分 .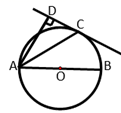 (1)、求证:DC为 的切线;(2)、若 ,求 的半径.27. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)、求证:DC为 的切线;(2)、若 ,求 的半径.27. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF. (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.28. 如图, 抛物线 经过点 , ,连接 ,点 是第一象限内抛物线上一动点.
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.28. 如图, 抛物线 经过点 , ,连接 ,点 是第一象限内抛物线上一动点. (1)、求抛物线的表达式;(2)、过点 作 轴的垂线,交 于点 ,判断是否存在点 ,使得以 、 、 为顶点的三角形是直角三角形,若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 与点 关于 轴对称,连接 , , ,当点 运动到什么位置时, 的面积最大?求 面积的最大值及此时点 的坐标.
(1)、求抛物线的表达式;(2)、过点 作 轴的垂线,交 于点 ,判断是否存在点 ,使得以 、 、 为顶点的三角形是直角三角形,若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 与点 关于 轴对称,连接 , , ,当点 运动到什么位置时, 的面积最大?求 面积的最大值及此时点 的坐标.