福建省厦门市湖里区2021年数学中考毕业班教学质量检测试卷
试卷更新日期:2021-09-16 类型:中考模拟
一、单选题
-
1. 2的算术平方根是( )A、 B、 C、 D、2. 一个几何体的正视图如图所示,则这个几何体可能为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,在数轴上 , , , 四个点中,点 最可能表示的实数是( ).
3. 如图,在数轴上 , , , 四个点中,点 最可能表示的实数是( ). A、 B、 C、 D、4. 科学家测得2019年新型冠状病毒(2019-nCoV)的大小约为 ,则数据 用科学记数法表示为( )A、 B、 C、 D、5. 将 化简得( )A、 B、 C、 D、6. 如图,点 , 在线段 上, 与 全等,点 和点 ,点 和点 是对应点, 和 交于点 ,则与 相等的线段是( )
A、 B、 C、 D、4. 科学家测得2019年新型冠状病毒(2019-nCoV)的大小约为 ,则数据 用科学记数法表示为( )A、 B、 C、 D、5. 将 化简得( )A、 B、 C、 D、6. 如图,点 , 在线段 上, 与 全等,点 和点 ,点 和点 是对应点, 和 交于点 ,则与 相等的线段是( )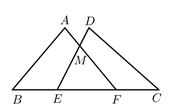 A、 B、 C、 D、7. 为迎接六一儿童节,SM莱雅百货商场进行促销活动,某种商品进价800元,出售标价1200元,本次打折销售要保证利润不低于5%,则最多可打( )A、六折 B、七折 C、八折 D、九折8. 三个顶点都在网格点上,且有一个角为直角的三角形称为网格直角三角形.在 的网格图中,若 为网格直角三角形,则满足条件的 点个数有( )
A、 B、 C、 D、7. 为迎接六一儿童节,SM莱雅百货商场进行促销活动,某种商品进价800元,出售标价1200元,本次打折销售要保证利润不低于5%,则最多可打( )A、六折 B、七折 C、八折 D、九折8. 三个顶点都在网格点上,且有一个角为直角的三角形称为网格直角三角形.在 的网格图中,若 为网格直角三角形,则满足条件的 点个数有( ) A、6 B、7 C、13 D、159. 如图是一个长为 ,宽为 的矩形,用剪刀沿矩形的两条对称轴剪开,把它分成四个全等的小矩形,然后按图6拼成一个正方形,则中间空白部分的面积是( )
A、6 B、7 C、13 D、159. 如图是一个长为 ,宽为 的矩形,用剪刀沿矩形的两条对称轴剪开,把它分成四个全等的小矩形,然后按图6拼成一个正方形,则中间空白部分的面积是( )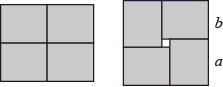 A、 B、 C、 D、10. 已知函数 ( 为常数, )的图象经过点 ,且实数 , , 满足等式: ,则一次函数 与 轴的交点坐标为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知函数 ( 为常数, )的图象经过点 ,且实数 , , 满足等式: ,则一次函数 与 轴的交点坐标为( )A、 B、 C、 D、二、填空题
-
11. 不等式组 的解集为.12. 若 ,则 的余角是.13. 在一个不透明的袋子里有1个黑球2个白球,这些球除颜色外都相同,从袋子中随机摸出两个球,则摸到两个均为白球的概率是.14. 在平面直角坐标系中, 轴,点 , ,则点 的坐标为.15. 如图,在 中, , , 分别为边 , 上的点( , 不与端点重合).对于任意 ,下面四个结论:
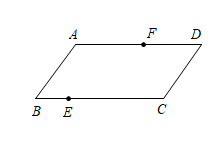
①存在无数个平行四边形 ;②至少存在一个菱形 ;③至少存在一个矩形 ;④存在无数个面积是 面积的一半的四边形 .所有正确结论的序号是.
16. 如图, 是双曲线 在第二象限上的一动点, 的延长线与双曲线的另一支相交于点 ,取点 在第一象限,且 ,则 的最小值为.
三、解答题
-
17. 计算: .18. 如图,在矩形 中, ,且交 的延长线于点 .求证: .
 19. 先化简,再求值: ,其中 .20. 一个四边形的对角线相等,则称这个四边形是对等四边形.
19. 先化简,再求值: ,其中 .20. 一个四边形的对角线相等,则称这个四边形是对等四边形.证明:圆内接对等四边形有一组对边平行.
21. 公司员工甲去距离单位6千米的社区医院接种新冠疫苗,去时骑自行车,在医院等候和接种疫苗花了2小时,回来时发现时间可能来不及了,改乘汽车返回公司,已知其骑自行车的速度不超过 ,汽车的速度是骑自行速度的1.5倍,并且公司规定在离开之时算起2.5小时内需返回公司.问甲能否规定时间内及时返回公司?22. 如图,在 中, , , 是 的外接圆,连接 并延长交 于点 ,连接 ,点 是 的内心. (1)、请用直尺和圆规作出点 ,证明 ;(2)、求线段 长.23. 为迎接党的百年庆典,某街道党委举办了一次“学史明理,学史崇德”党史知识答题测试,成绩等级划分规则如下表所示,成绩越好等级越高.
(1)、请用直尺和圆规作出点 ,证明 ;(2)、求线段 长.23. 为迎接党的百年庆典,某街道党委举办了一次“学史明理,学史崇德”党史知识答题测试,成绩等级划分规则如下表所示,成绩越好等级越高.分数
等级
某社区参加知识答题测试的党员数共有300人,抽取50个党员,他们的答题成绩中没有 等级的,绘制了如图1,图2所示统计图表.
 (1)、补全条形统计图,扇形图中等级 所对圆心角为 ▲ °,本次调查中的样本是 ▲ .(2)、求该社区党员的答题平均成绩,并解释它的实际意义;(3)、若成绩在 级以及以下级别的党员需要参加第二轮答题,求该社区需要参加第二轮答题的党员数?24. 已知, 是 的外接圆,点 和点 在 外, , , , 分别交 于点 和点 ,且点 是弧 的中点.(1)、如图,求证: 的圆心 在线段 上;
(1)、补全条形统计图,扇形图中等级 所对圆心角为 ▲ °,本次调查中的样本是 ▲ .(2)、求该社区党员的答题平均成绩,并解释它的实际意义;(3)、若成绩在 级以及以下级别的党员需要参加第二轮答题,求该社区需要参加第二轮答题的党员数?24. 已知, 是 的外接圆,点 和点 在 外, , , , 分别交 于点 和点 ,且点 是弧 的中点.(1)、如图,求证: 的圆心 在线段 上;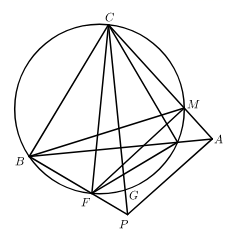 (2)、如图,连接 交 与于点 ,交 与于点 ,连接 ,交 于点 ,连接 并延长 ,交 于点 ,若 , 时,请你探究线段 , 之间的数量关系.
(2)、如图,连接 交 与于点 ,交 与于点 ,连接 ,交 于点 ,连接 并延长 ,交 于点 ,若 , 时,请你探究线段 , 之间的数量关系. 25. 已知:抛物线 与 轴相交于 , 两点(点 在点 的左边)与 轴相交于点 ,且 .(1)、求该抛物线的解析式;(2)、已知 和 都在抛物线上,若 ,求 的取值范围;(3)、在(1)的条件下, 是抛物线的顶点,直线 与直线 相交于点 ,连接 .若点 ,点 在 轴上方,对称轴右侧的抛物线上,连接 交 于点 ,且 ,求点 坐标
25. 已知:抛物线 与 轴相交于 , 两点(点 在点 的左边)与 轴相交于点 ,且 .(1)、求该抛物线的解析式;(2)、已知 和 都在抛物线上,若 ,求 的取值范围;(3)、在(1)的条件下, 是抛物线的顶点,直线 与直线 相交于点 ,连接 .若点 ,点 在 轴上方,对称轴右侧的抛物线上,连接 交 于点 ,且 ,求点 坐标