湖南省长沙市长郡教育集团2021-2022学年八年级上学期数学开学试卷

试卷更新日期：2021-09-16 类型：开学考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，在第三象限的点是（）

A、（-3，5） B、（1，-2） C、（-2，-3） D、（1，1）

查看试题解析
2. 如图，AB⊥CD，垂足为O，EF是过点O的一条直线，已知∠1=40°，则∠2=（）

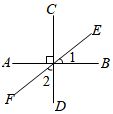A、40° B、45° C、50° D、60°

查看试题解析
3. 已知点P（2a+6，4+a）在第二象限，则a的取值范围是（）

A、 $- 4 < a < - 3$ B、 $a < - 3$ C、 $a > - 3$ D、 $a > - 4$

查看试题解析
4. 下列调查中，调查方式选择合理的是（）.

A、为了了解我市居民平均每日废弃口罩的数量，选择全面调查 B、为了了解某一批次LED灯泡的使用寿命，选择抽样调查 C、为了了解中国空间站“天和”核心舱的设备零件质量情况，选择抽样调查 D、为了了解我市七年级学生参加社会实践的时间，选择全面调查

查看试题解析
5. 已知一个多边形的内角和是1080°，则该多边形的边数为（）

A、4 B、6 C、8 D、10

查看试题解析
6. 下列各式正确的是（）

A、 $\sqrt{{(- 7)}^{2}} = - 7$ B、 $\sqrt{9} = \pm 3$ C、 $\sqrt[3]{- 5} = \sqrt[3]{5}$ D、 $\sqrt{64} - \sqrt[3]{64} = 4$

查看试题解析
7. 如图，下列判断正确的是（）

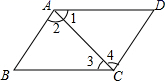A、若 $∠ 1 = ∠ 3$ ，则 $A B // D C$ B、若 $∠ A B C = ∠ A D C$ ，则 $A D // B C$ C、若 $∠ A B C + ∠ B C D = 180 °$ ，则 $A D // B C$ D、若 $∠ 2 = ∠ 4$ ，则 $A B // D C$

查看试题解析
8. 如果 a＞b，那么下列各式中正确的是（）

A、a＋1＜b＋1 B、－a＋3＜－b＋3 C、－a＞－b D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
9. 如图，在 $△ A B C$ 和 $△ D C B$ 中， $∠ A B C = ∠ D C B$ ，再添加一个条件，不能证明 $△ A B C$ 和 $△ D C B$ 全等的是（）

A、 $∠ A C B = ∠ D B C$ B、 $∠ A = ∠ D$ C、 $A B = C D$ D、 $A C = D B$

查看试题解析
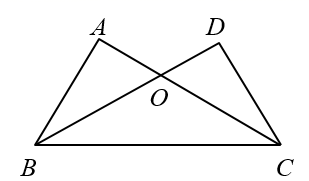10. 中国古代人民在生产生活中发现了许多数学问题，在《九章算术》中记载了这样一个问题，大意为：“今有5只雀、6只燕，分别聚集而且用衡器称之，聚在一起的雀重，燕轻.将一只雀、一只燕交换位置而放，则衡器两边的总重量相等，如果5只雀和6只燕的总重量为1斤，问雀、燕每1只各重多少斤？”如果设每只雀重x斤，每只燕重y斤，则下列方程组正确的是（）

A、 ${\begin{array}{l} 5 x + y = 4 y + x \\ 5 x + 6 y = 1 \end{array}$ B、 ${\begin{array}{l} 4 x + y = 5 y + x \\ 5 x + 6 y = 1 \end{array}$ C、 ${\begin{array}{l} 5 x + y = 4 y + x \\ 6 x + 5 y = 1 \end{array}$ D、 ${\begin{array}{l} 4 x + y = 5 y + x \\ 6 x + 5 y = 1 \end{array}$

查看试题解析
11. 在下列条件：①∠A+∠B＝∠C，②∠A：∠B：∠C＝5：3：2，③∠A＝90°﹣∠B，④∠A＝2∠B＝3∠C中，能确定△ABC是直角三角形的条件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的个数（）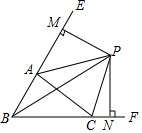

①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB=2∠APB；④S_△PAC=S_△MAP+S_△NCP.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

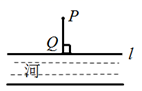
13. 如图，要把河中的水引到农田P处，想要挖的水渠最短，我们可以过点P作PQ垂直河边l，垂足为点Q，然后沿PQ开挖水渠，其依据是.

查看试题解析
14. 把方程 $5 x - 2 y = 3$ 改写成用含 $x$ 的式子表示 $y$ 的形式是：.

查看试题解析
15. 如图，则∠A+∠B+∠C+∠D+∠E的度数是.

查看试题解析
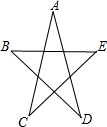16. 如图，△ABC≌△DBE，△ABC的周长为30，AB＝9，BE＝8，则AC的长是.

查看试题解析
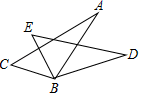17. 在△ABC中，AC＝5，中线AD＝7，则AB边的取值范围是.

查看试题解析
18. 如图，在△ABC中，∠ACB=90，AC=6，BC=8.点P从点A出发，沿折线AC—CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发.分别过P、Q两点作PE⊥l于E，QF⊥l于F，当△PEC与△QFC全等时，CQ的长为.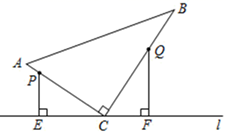

查看试题解析

三、解答题

19. 计算： $| 7 - \sqrt{2} | - | \sqrt{2} - π | - \sqrt{{(- 7)}^{2}}$ .

查看试题解析
20. 解二元一次方程组： ${\begin{array}{l} 2 x - 3 y = - 3 \\ - 4 x + y = - 3 \end{array}$ .

查看试题解析
21. 解不等式： $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} > 1$ ，并把它的解集表示在数轴上.

查看试题解析
22. 按要求画图及填空：
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系，原点O及△ABC的顶点都在格点上．

(1)、点A的坐标为；

(2)、将△ABC先向下平移2个单位长度，再向右平移5个单位长度得到△A₁B₁C₁ ，画出△A₁B₁C₁ ．

(3)、△A₁B₁C₁的面积为．

查看试题解析
23. 某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩（满分为100分，得分均为整数）进行统计，绘制了图中两幅不完整的统计图.根据图中信息，回答下列问题：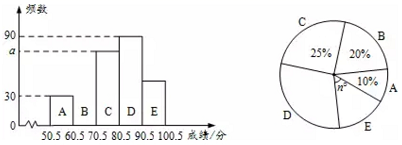

(1)、a= ， n=；

(2)、补全频数分布直方图；

(3)、该校共有2000名学生.若成绩在80分以上的为优秀，请你估计该校成绩优秀的学生人数.

查看试题解析
24. 如图，已知点A在EF上，点P，Q在BC上，∠E=∠EMA，∠BQM=∠BMQ.

(1)、求证：EF//BC；

(2)、若∠3+∠4=180°， $∠ B A F = 3 ∠ F - 20 °$ ，求∠B的度数.

查看试题解析
25. 如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°，求：∠DAC和∠BOA的度数．

查看试题解析
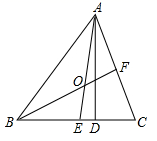26. 如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD，

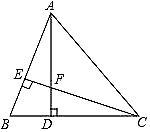(1)、求证：△ABD≌△CFD；

(2)、已知BC=7，AD=5，求AF的长。

查看试题解析
27. 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆，如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨，每辆B型货车最多可装甲种货物5吨和乙种货物7吨.

(1)、装货时按此要求安排A、B两种货车的辆数，共有几种方案？

(2)、使用A型车每辆费用为600元，使用B型车每辆费用800元.在上述方案中，哪个方案运费最省？最省的运费是多少元？

(3)、在（2）的方案下，现决定对货车司机发共2100元的安全奖，已知每辆A型车奖金为m元.每辆B型车奖金为n元，38＜m＜n.且m、n均为整数，求此次奖金发放的具体方案.

查看试题解析
28. 在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C.且BD=CD，点E，F分别在边AM和AN上.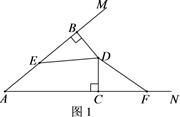

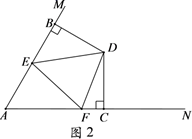(1)、如图1，若∠BED=∠CFD，请说明DE=DF；

(2)、如图2，若∠BDC=120°，∠EDF=60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由.

查看试题解析
29. 对于平面直角坐标系 $x O y$ 中的点P（a，b），若点P'的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），则称点P'为点P的“k属派生点”.例如：P（1，4）的“2属派生点”为P'（1+2×4，2×1+4），即P'（9，6）.

(1)、若点P的“3属派生点”P'的坐标为（6，2），求点P的坐标；

(2)、若点P在x轴的正半轴上，点P的“k属派生点”为P'点，且线段PP'的长度为线段OP长度的2倍，求k的值；

(3)、如图，已知点A（0，2），点P是x轴上一点，且是点（2，4）的“k属派生点”，以线段AP为一边，在其一侧作如图所示等边三角线APQ.现P点沿x轴运动，当点P运动到原点O处时，记Q的位置为B.问三角形ABQ的面积是否是一个定值，如果是，请求出面积；如果不是，请说明理由.

查看试题解析