河南省驻马店市上蔡县2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-16 类型：期中考试

进入出卷网下载

一、单选题

1. 如果向右走5步记为＋5，那么向左走3步记为（）

A、－3 B、＋3 C、＋2 D、－2

查看试题解析
2. 下列各组数中，互为相反数的有（）
① $- (- 2)$ 和 $- | - 2 |$ ；② ${(- 1)}^{2}$ 和 $- 1^{2}$ ；③ $2^{3}$ 和 $3^{2}$ ；④ ${(- 2)}^{3}$ 和 $- 2^{3}$

A、①② B、②③ C、①④ D、①②④

查看试题解析
3. 把（+3）﹣（+5）﹣（﹣1）+（﹣7）写成省略括号的和的形式是（）.

A、﹣3﹣5+1﹣7 B、3﹣5﹣1﹣7 C、3﹣5+1﹣7 D、3+5+1﹣7

查看试题解析
4. 舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约499.5亿千克，这个数用科学记数法应表示为（）

A、4.995×10¹¹ B、49.95×10¹⁰ C、0.4995×10¹¹ D、4.995×10¹⁰

查看试题解析
5. 实数a在数轴上对应的点如图所示，则a、－a、1的大小关系正确的是（）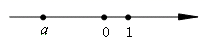

A、－a＜a＜1 B、a＜－a＜1 C、1＜－a＜a D、a＜1＜－a

查看试题解析
6. 计算3 $\frac{1}{4}$ +（–2 $\frac{3}{5}$ ）+5 $\frac{3}{4}$ +（–8 $\frac{2}{5}$ ）时，运算律用得最为恰当的是（）

A、[3 $\frac{1}{4}$ +（–2 $\frac{3}{5}$ ）]+[5 $\frac{3}{4}$ +（–8 $\frac{2}{5}$ ）] B、（3 $\frac{1}{4}$ +5 $\frac{3}{4}$ ）+[–2 $\frac{3}{5}$ +（–8 $\frac{2}{5}$ ）] C、[3 $\frac{1}{4}$ +（–8 $\frac{2}{5}$ ）]+（–2 $\frac{3}{5}$ +5 $\frac{3}{4}$ ） D、（–2 $\frac{3}{5}$ +5 $\frac{3}{4}$ ）+[3 $\frac{1}{4}$ +（–8 $\frac{2}{5}$ ）]

查看试题解析
7. 用四舍五入法对3.8963取近似数，精确到0.01，得到的正确结果是（　　）

A、3.89 B、3.9 C、3.90 D、3.896

查看试题解析
8. 下列说法错误的是（）

A、 $- \frac{x y^{2}}{5}$ 的系数是 $- \frac{1}{5}$ B、 $\frac{2 x^{2} y^{3} z}{3}$ 的次数是5 C、1是单项式 D、单项式和多项式统称整式

查看试题解析
9. 对于多项式 $x^{3} + x^{2} - 1$ ，下列说法错误的是（）

A、它的常数项是－1 B、它是关于 $x$ 的三次三项式 C、它是按 $x$ 的降幂排列 D、当 $x = - 1$ 时，它的值为－3

查看试题解析

10. 根据加密的基本过程就是对原来为明文的文件或数据按某种算法进行处理，使其成为不可读的一段代码为“密文”，他人只能在输入相应的密钥之后才能获取原文，通过这样的途径来达到保护数据不被非法窃取，阅读的目的.有这样一种加密算法，将英文26个字母（不论大小写）依次对应

1 ， 2 ， 3 ， \cdot \cdot \cdot ， 26

，这26个序号（见表格），当数据中明码对应的序号

x

为奇数时，密码对应的序号为

\frac{1}{2} (x + 3)

，当数据中明码对应的序号

x

为偶数时，密码对应的序号为

\frac{x}{2} + 14

，按照此规定，将明码“

h o p e

”译成密码为（）

字母	$a$	$b$	$c$	$d$	$e$	$f$	$g$	$h$	$i$	$j$	$k$	$l$	$m$
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
字母	$n$	$o$	$p$	$q$	$r$	$s$	$t$	$u$	$v$	$w$	$x$	$y$	$z$
序号	14	15	16	17	18	19	20	21	22	23	24	25	26

A、

g s w q

B、

r i v d

C、

g i h e

D、

h o p e

查看试题解析

二、填空题

11. 写出一个小于－1且大于－2的数：.

查看试题解析
12. 如果一个数的平方等于它的本身，则这个数是．

查看试题解析
13. 数轴上，点 $A$ 表示的数是－3，距点 $A$ 为4个单位长度的点所表示的数是.

查看试题解析
14. 若a，b互为相反数，c，d互为倒数，且|c|＝1，则 $\frac{a + b}{c}$ ＋c²－cd的值为.

查看试题解析
15. 下列是有规律排列的一列数： $- \frac{1}{2} ， \frac{2}{4} ， - \frac{3}{8} ， \frac{4}{16} ， - \frac{5}{32}$ ，…，请观察此一列数，按此规律，第n个数应是.

查看试题解析

三、解答题

16. 计算：

(1)、 $(- 8) + (- \frac{1}{4}) - (+ 5) - (- 0.25)$

(2)、 $2 - 2 \div \frac{1}{3} \times 3$

(3)、 $[1 - (1 - 0.5 \times \frac{1}{3})] \times [2 - {(- 3)}^{2}]$

(4)、 $- 4^{2} \div (- 32) - [{(- \frac{2}{3})}^{2} \times (- 3^{2}) + (- \frac{11}{3})]$

查看试题解析
17. 请你结合自身生活实际，设计具体情境，解释下列代数式的意义：

(1)、 $(1 - 20 %) x$

(2)、 $a^{3}$

(3)、 $\frac{30}{m}$

(4)、 $\frac{3 a + 2 b}{5}$

查看试题解析
18. 某公路养护小组乘车沿南北向进行公路巡视维护：某早晨从 $A$ 地出发，晚上最后到达 $B$ 地，若约定向北为正方向，当天的行驶记录如下（单位：km）：
$+ 15 ， - 2 ， + 5 ， - 1 ， + 10 ， - 3 ， - 2 ， + 12 ， + 4 ， - 5 ， + 6$ .

(1)、问 $B$ 地在 $A$ 地的哪个方向？它们相距多少千米？

(2)、如果汽车行驶每千米耗油 $a$ 升，那么该天共耗油多少升？

查看试题解析
19. 如图，在数轴上的点 $A$ 、 $B$ 、 $O$ 、 $C$ 、 $D$ 分别表示－5、－1.5、0、2.5、5，回答下列问题：

(1)、 $B$ 、 $C$ 两点的距离是多少？ $A$ 、 $B$ 两点间的距离是多少？

(2)、若点 $M$ 、 $N$ 也在这条数轴上，且点 $M$ 、 $N$ 分别表示的数为 $m$ 、 $n$ ，则点 $M$ 、 $N$ 两点间的距离是多少？

查看试题解析
20. 阅读下列材料：计算 $50 \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12})$
解法一：原式= $50 \div \frac{1}{3} - 50 \div \frac{1}{4} + 50 \div \frac{1}{12} = 50 \times 3 - 50 \times 4 + 50 \times 12 = 550$ ．

解法二：原式= $50 \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) = 50 \div \frac{2}{12} = 50 \times 6 = 300$ ．

解法三：原式的倒数为 $(\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \div 50 = (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \times \frac{1}{50} = \frac{1}{3} \times \frac{1}{50} - \frac{1}{4} \times \frac{1}{50} + \frac{1}{12} \times \frac{1}{50} = \frac{1}{300}$

故原式=300．

上述得出的结果不同，肯定有错误的解法，你认为解法 ▲ 是错误的．

请你选择合适的解法解答下列问题：计算： $(- \frac{1}{42}) \div (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7})$

查看试题解析
21. 若 $a$ ， $b$ 是有理数，定义一种运算“ $\otimes$ ”： $a \otimes b = a b - 2 a - 2 b + 1$ ，

(1)、计算 $3 \otimes (- 2)$ 的值；

(2)、计算 $[(- 4) \otimes 2] \otimes (- 3)$ 的值；

(3)、定义的新运算“ $\otimes$ ”对交换律是否成立？请写出你的探究过程.

查看试题解析
22. 小华学了有理数的乘方后，知道了 $2^{1} = 2 ， 2^{2} = 4 ， 2^{3} = 8 ， 2^{4} = 16 ， 2^{5} = 32 ， \cdot \cdot \cdot$ .
她问老师：“有没有 $2^{0}$ 和 $2^{- 3}$ ，如果有，那结果等于多少？”

老师提示他：“ $2^{5} \div 2^{3} = 4$ ， $2^{5 - 3} = 2^{2} = 4$ ，于是 $2^{5} \div 2^{3} = 2^{5 - 3} = 4$ ，……”

小华说：“噢，我明白了！”

很快地，小华就算出了 $2^{0}$ 和 $2^{- 3}$ 的结果了。

亲爱的同学们，你想出来了吗？

(1)、请你根据老师的提示，算一算 $2^{0}$ 和 $2^{- 3}$ 的值；

(2)、据此比较 ${(- 3)}^{- 2}$ 和 ${(- 2)}^{- 3}$ 的大小.（写出计算过程）

查看试题解析
23. 某商店售乒乓球拍和乒乓球，乒乓球拍每只定价50元，乒乓球每个定价2元，商家为促销商品，同时向客户提供两种优惠方案：①买1只乒乓球拍送5个乒乓球；②乒乓球拍和乒乓球都按照定价的九折优惠.现在某客户要到该商店购买乒乓球拍20只，乒乓球 $x$ 个 $(x > 100)$ .

(1)、若该客户按优惠方案①购买需付款元；（用含 $x$ 的式子表示）

(2)、若该客户按优惠方案②购买需付款元；（用含 $x$ 的式子表示）

(3)、当 $x = 400$ 时，在这两种优惠方案中，请通过计算说明，此时按哪一种优惠方案购买较为合算？

(4)、若 $x = 800$ ，请你设计一个最优惠的购买方案，使得该客户花费最少，并计算需付的钱数.

查看试题解析