河南省郑州市中牟县2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数都是正数或都是负数的是（）

A、1，2，3 B、-9，0，2 C、-1，2，-3 D、0，-1，-2

查看试题解析
2. 若一个圆的半径为 $r - 8$ ，那么该圆的面积 $S$ 等于（）

A、 $π r^{2}$ B、 $2 π r^{2}$ C、 $π {(r - 8)}^{2}$ D、 $2 π {(r - 8)}^{2}$

查看试题解析
3. 节约是一种美德，节约是一种智慧.据不完全统计，全国每年浪费食物总量折合成粮食可养活约3亿5千万人.3亿5千万用科学记数法表示为（）

A、 $3.5 \times 10^{6}$ B、 $3.5 \times 10^{7}$ C、 $3.5 \times 10^{8}$ D、 $3.5 \times 10^{9}$

查看试题解析
4. 有理数 $a^{2} = {(- 5)}^{2}$ ，则 $a$ 等于（）

A、-5 B、5 C、25 D、 $\pm 5$

查看试题解析
5. 小明做了下列3道计算题：
① $\frac{1}{2} - \frac{1}{2} \times 2 = 0 \times 2 = 0$ ，② $- 2^{3} - {(- 3)}^{2} = - 8 - 9 = - 17$ ，③ $6 \div (\frac{3}{2} - \frac{2}{3}) = 6 \div \frac{3}{2} - 6 \div \frac{2}{3} = 9 - 6 = 3$ .其中正确的有（）

A、0道 B、1道 C、2道 D、3道

查看试题解析
6. 下列说法中，错误的是（）

A、 $m$ 是单项式也是整式 B、单项式 $\frac{2}{7} x^{2} y$ 的系数是 $\frac{1}{7}$ ，次数是2 C、整式不一定是多项式 D、多项式 $2 x^{2} - x y^{2} + 3^{3}$ 是三次三项式

查看试题解析
7. 一个物体的外形是长方体（如图（1）），其内部构造不祥.用平面横向自上而下截这个物体时，得到了一组截面，截面形状如图（2）所示，这个长方体的内部构造是（）

A、圆柱 B、球 C、圆锥 D、圆柱或球

查看试题解析
8. 从 $x < 0$ ， $y > 0$ ， $x + y < 0$ ，那么下列关系中正确的是（）

A、 $- x < - y < x < y$ B、 $- y < x < y < - x$ C、 $x < - y < - x < y$ D、 $x < - y < y < - x$

查看试题解析
9. 如图是一个运算程序的示意图，若开始输入 $x$ 的值为81，则第2020次输出的结果为（）

A、3 B、27 C、9 D、1

查看试题解析
10. 从1开始得到如下的一列数1，2，4，8，16，22，24，28，36，…其中每一个数加上自己的个位数，成为下一个数，上述这一列数中小于100的个数为（）

A、15 B、21 C、50 D、99

查看试题解析

二、填空题

11. 我国现采用国际通用的公历纪年法，如果我们把公元2013年记作+2013年，那么，处于公元前500年的春秋战国时期可表示为年.

查看试题解析
12. 若代数式 $a x + b x$ 合并同类项后结果为零，则 $a$ ， $b$ 满足的关系式是.

查看试题解析
13. 如图是由几个大小相同的小立方块搭成的几何体，搭成这个几何体需要10个小立方块，在保持从正面看和从左面看到的形状图不变的情况下，最多可以拿掉个小立方块.

查看试题解析
14. $a$ ， $b$ 互为相反数， $a \neq 0$ ， $n$ 为自然数，则下列叙述正确的有个.
① $- a$ ， $- b$ 互为相反数；② $a^{n}$ ， $b^{n}$ 互为相反数；

③ $a^{2 n}$ ， $b^{2 n}$ 互为相反数；④ $a^{2 n + 1}$ ， $b^{2 n + 1}$ 互为相反数.

查看试题解析
15. 把四张形状大小完全相同的小长方形卡片（如图1）不重叠地放在一个底面为长方形（长为 $a cm$ ，宽为 $b cm$ ）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长之和是.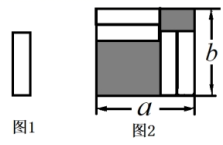

查看试题解析

三、解答题

16.

(1)、计算： ${(- 3)}^{2} \times 6 \div [{(- 2)}^{2} + 2 \times (- 5)]$ ；

(2)、计算： $[{(- 1)}^{2019} - (\frac{3}{2} - \frac{5}{6} - \frac{1}{9}) \times 18] \div | - 2^{2} |$ .

查看试题解析
17. 先化简，再求值： $4 (a^{2} - a b) - 5 (b^{2} - \frac{4}{5} a b)$ ，其中 $a = - 2$ ， $b = 2$ ．

查看试题解析
18. 小明在电脑中设置了一个有理数的运算程序：输入数 $a$ ，加 $*$ 键，再输入数 $b$ ，就可以得到运算： $a * b = (a - b) - | b - a |$ .如 $1 * 2 = (1 - 2) - | 2 - 1 | = - 1 - 1 = - 2$ .

(1)、计算 $- 3 * 2$ 的值；

(2)、当 $a$ ， $b$ 在数轴上的位置如图所示时，求 $a * b$ 的值.

查看试题解析

19. 观察表中几何体，解答下列问题：

名称	三棱柱	四棱柱	五棱柱	六棱柱
图形
顶点数 $a$	6	_________	10	12
棱数 $b$	9	12	_________	18
面数 $c$	5	6	7	_________

(1)、补全表中数据；

(2)、观察表中的结果，试用含有

n

的代数式表示

n

棱柱的顶点数：，棱数：，面数：；

(3)、观察表中的结果，你发现

a

，

b

，

c

之间存在什么关系？请写出关系式.

查看试题解析

20. 聪聪在学习了“展开与折叠”这一课后，明白了很多几何体都能展开成平面图形，于是他在家用剪刀把一个长方体纸盒（如图（1））剪开了，可是他一不小心多剪了一条棱，把纸盒剪成了两部分，即图（2）中的①和②.根据你所学的知识，回答下列问题：

(1)、若这个长方体纸盒的长、宽、高分别是 $8 cm$ ， $4 cm$ ， $2 cm$ ，则该长方体纸盒的体积是多少？

(2)、聪聪一共剪开了条棱；

(3)、现在聪聪想将剪掉的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪掉的②粘贴到①中的什么位置？请你帮助他在①上补全一种情况.

查看试题解析
21. 某商店出售一种商品，其原价为 $a$ 元，有如下两种调价方案：方案一是先提价 $15 %$ ，在此基础上又降价 $15 %$ ；方案二是先降价 $15 %$ ，在此基础上又提价 $15 %$ .

(1)、用这两种方案调价后的价格分别是多少？结果是否一样？调价后的结果是不是都恢复了原价？

(2)、两种调价方案改为：方案一是先提价 $25 %$ ，在此基础上又降价 $25 %$ ；方案二是先降价 $25 %$ ，在此基础上又提价 $25 %$ .这时结果怎样？

(3)、你能总结出什么结论呢？

查看试题解析
22.

(1)、若 ${(a + 2)}^{2} + | b - 3 | = 0$ ，求 $a^{b}$ 的值.

(2)、观察下列等式：
$1^{3} = 1^{2}$ ， $1^{3} + 2^{3} = 3^{2}$ ， $1^{3} + 2^{3} + 3^{3} = 6^{2}$ ， $1^{3} + 2^{3} + 3^{3} + 4^{3} = 10^{2}$ ， $1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} = 15^{2}$ ，…

①想一想，等式左边各项幂的底数与右边幂的底数有什么关系？

②探索上面式子的规律，试用含 $n$ 的式子表示第 $n$ 个等式；

③请你用可能出现的第六个等式进行验证.

查看试题解析

23. 十一黄金周期间，南京市中山陵风景区在8天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：

日期	1日	2日	3日	4日	5日	6日	7日	8日
人数变化单位：万人	1.2	－0.2	0.8	－0.4	0.6	0.2	$a$	－1.2

注：9月30日的游客人数为2万人.

(1)、10月1日至5日这五天中游客人数最多的是10月日.

(2)、求10月1日至5日这五天的游客总人数是多少万人.

(3)、若10月8日到该风景区旅游的游客人数与9月30日的游客一样多，求表格中

a

的值.

查看试题解析